主成分分析

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

（协方差矩阵详细解释：协方差矩阵与相关性分析 - 知乎 (zhihu.com)）

那么我们如何得这个方差最大的主成分方向呢，最经典的方法是特征值分解协方差矩阵，得到协方差矩阵的特征值和特征向量，选择特征值最大（即方差最大的）k个特征向量组成的矩阵。这样就实现了从n维到k维的数据降维。

这里先证明一下为什么协方差矩阵中特征值最大的方向对应的方差最大。

协方差矩阵特征值的几何意义 - 知乎 (zhihu.com)

知道这一点之后就可以很容易的得到基于特征值分解的PCA算法流程了。

输入：数据集X需要降到k维。

1) 去平均值(即去中心化)，即每一位特征减去各自的平均值。

2) 计算协方差矩阵 注：这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。

3) 用特征值分解方法求协方差矩阵  的特征值与特征向量。

4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5) 将数据转换到k个特征向量构建的新空间中，即。

参考：主成分分析（PCA）原理详解 - 知乎 (zhihu.com)

举个例子，对一个二维高斯分布的数据：

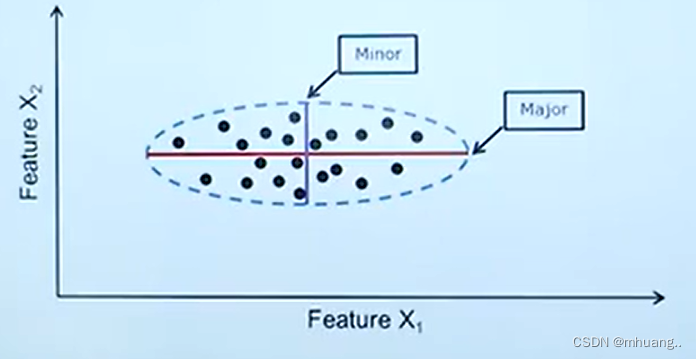
显然轴方差更大，所以如果要选一个特征作为划分标准的话，那么用X1的信息更加丰富，在上做类别划分效果更好。

对于一个不是标准垂直与坐标轴分布的数据， 那么为了像上面一样直观的区分特征，需要对坐标轴旋转变成，（这里做了一个平移到原点的处理，不影响分析），就变成了上面的情况。

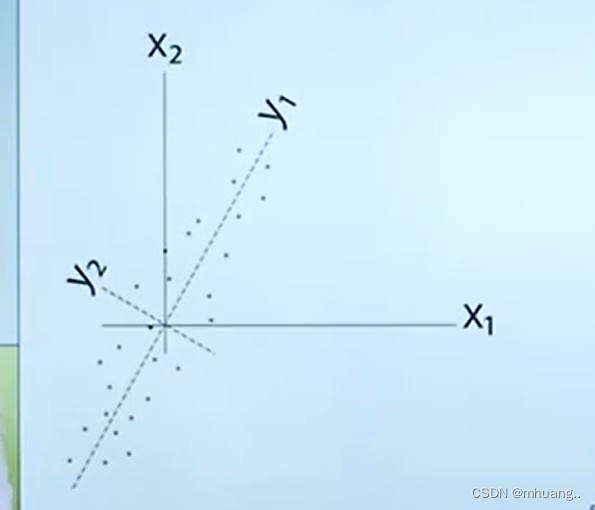
那么如何将，旋转到，呢？ 

设原本的散点数据协方差矩阵为：

  ，

对其做旋转变换可以得到

，

此时，其中。

由上式可知:

显然与特征值相同，令为单位矩阵且PQ均正交，则：

此时该旋转变化为，就是特征向量组成的矩阵。，就是包含信息最多的两个特征维度，这个过程其实就是主成分分析。

那么为什么，是包含信息最多的特征维度呢？

首先对于这个二维平面来说，我们任意划两个相互垂直的轴都可以作为这堆点数据的特征，将数据降维映射到特征轴上就是亮化后的信息，如图所示，散点映射到特征轴上后就可以沿着特征轴做进一步操作。

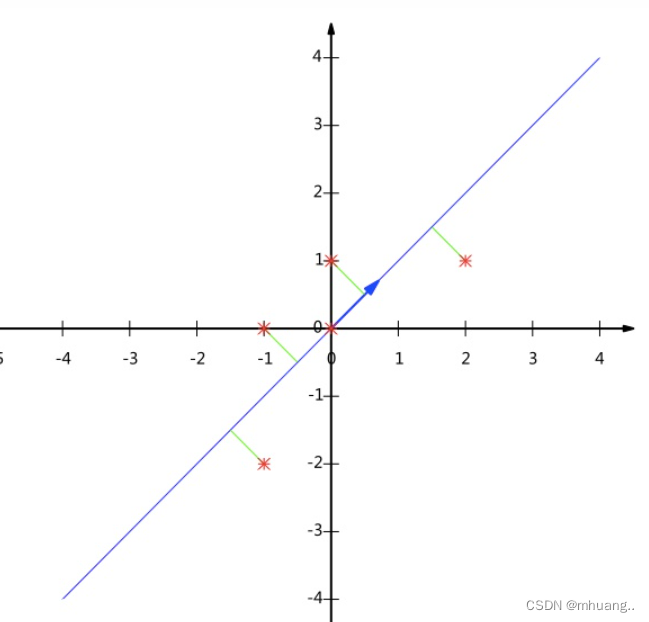
根据特征选择的原理，我们认为方差越大对应的信息越丰富，换句话说，我们需要找到一个合适的特征使得映射在这个特征上的数据信息损失尽可能的少。比如在下图将数据映射到v和映射到u上信息损失的程度是明显不一样的。 

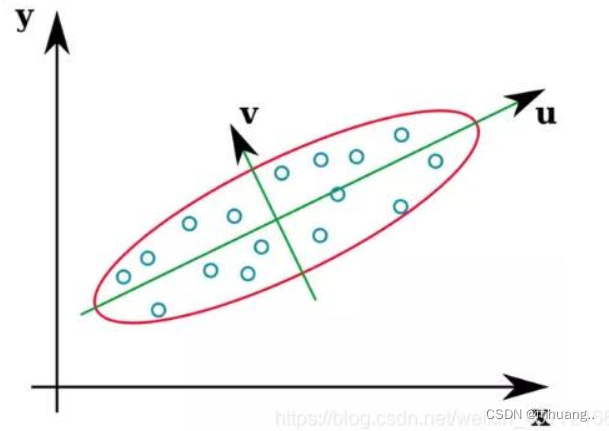
我们需要找到信息损失最少的特征， 设数据中某个散点向量在向量e上的投影为，e是任意一个特征轴的单位向量。

 

令，为了使得信息损失最少，我们需要最小化。

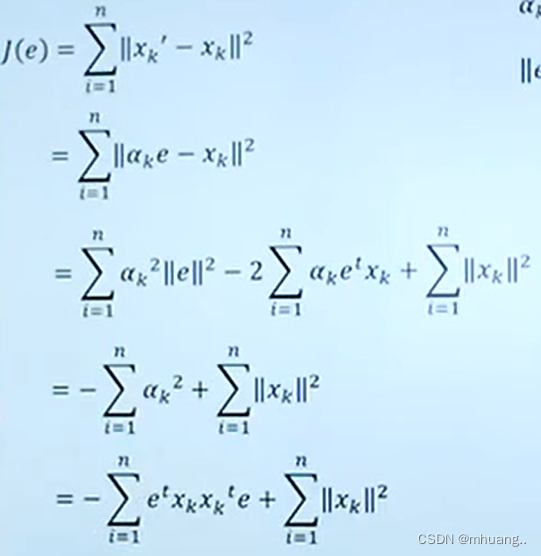
令，最小化就可以看成：

 我们用拉格朗日乘数法解这个约束函数：

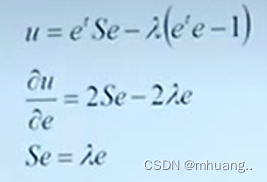
由可知，e和分别为矩阵S的特征向量和特征值。

此时

所以为了最小化，我们需要使得值最大。 所以我们需要将数据投影到特征值最大的特征向量e上，这就是PCA主成分分析的原理。

参考视频：15.2.6.1 主成分分析_哔哩哔哩_bilibili