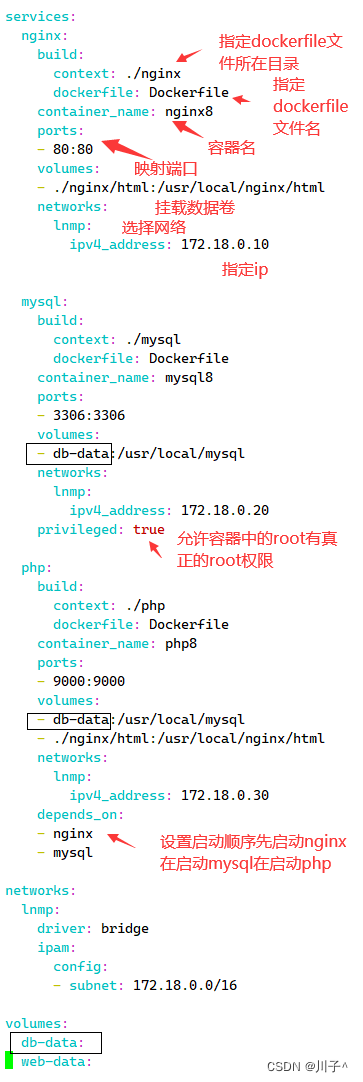
1.简述

      

基本思想
黄金分割法也称为 0.618 法，其基本思想是通过取试探点和进行函数值比较，使包含极小点的搜索区间不断缩短以逼近极小值点。适用于确定区间上的任何单谷函数求极小值的问题。

公式推导
设有定义在[ a , b ] [a,b][a,b]上的单谷函数
φ ( α ) = f ( x k + α d k ) \varphi \left( \alpha \right) =f\left( x_k+\alpha d_k \right)

在[ a , b ] [a,b][a,b]上取两个试探点。计算φ ( x 1 ) 
可能会出现以下两种情形：

我们要求试探点满足下列两个原则：

对称原则
λ = 新 区 间 长 度 原 区 间 长 度 = \lambda =\frac{新区间长度}{原区间长度}=λ= 
原区间长度
新区间长度
​
 =定值（保持缩减比）
从而可得
{ x 1 = a + ( 1 − λ ) ( b − a ) x 2 = a + λ ( b − a )

 

考虑情形1，此时新的搜索区间为[ a 1 , b 1 ] [a_1,b_1][a 
选取新的试探点x 
 

若令λ 2 = 1 − λ ( λ > 0 ) \lambda ^2=1-\lambda\left( \lambda>0 \right)λ 

则有
新的试探点x 4 x_4x 
1−λ得λ ≈ 0.618 \lambda \approx0.618λ≈0.618。

具体练习及Matlab实现
 

2.代码

主程序：

%%   用Opt_Golden()求解最优化
f1201 = inline('x-(x.*x-2).^3/2','x');
a = 0;
b = 4; 
TolX = 1e-4;%判断循环是否停止的x阈值
TolFun = 1e-4; %函数阈值
MaxIter = 100; %设定迭代次数
[xo,fo] = Opt_Golden(f1201,a,b,TolX,TolFun,MaxIter)

子程序：

function [xo,fo]=Opt_Golden(f,a,b,TolX,TolFun,k)
%%%%黄金搜索算法求在区间[a,b]上的最优化解
%f为目标函数，TolX为x阈值，TolFun为函数阈值，k为迭代次数
r =(sqrt(5)-1)/2; %r为黄金分割点值，
h = b-a;  %区间宽度
rh = r*h; 
%%%取两点c、d,并计算相应的函数值fc和fd
c = b-rh; 
d = a+rh;
fc = feval(f,c);
fd = feval(f,d);
%%%算法第二步判断是否停止迭代
if k <= 0 | (abs(h) < TolX & abs(fc - fd) < TolFun)
    if fc <= fd
        xo = c;
        fo = fc;
    else
        xo = d;
        fo = fd;
    end
    if k == 0
        fprintf('最好设定迭代次数大于0');
    end
%%%%算法第三步，进行新一轮迭代    
else
    if fc < fd
        [xo,fo] = Opt_Golden(f,a,d,TolX,TolFun,k-1);
    else
        [xo,fo] = Opt_Golden(f,c,b,TolX,TolFun,k-1);
    end
end

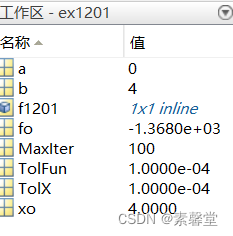
3.运行结果