机器学习-PCA主成份分析详细解说及代码实现

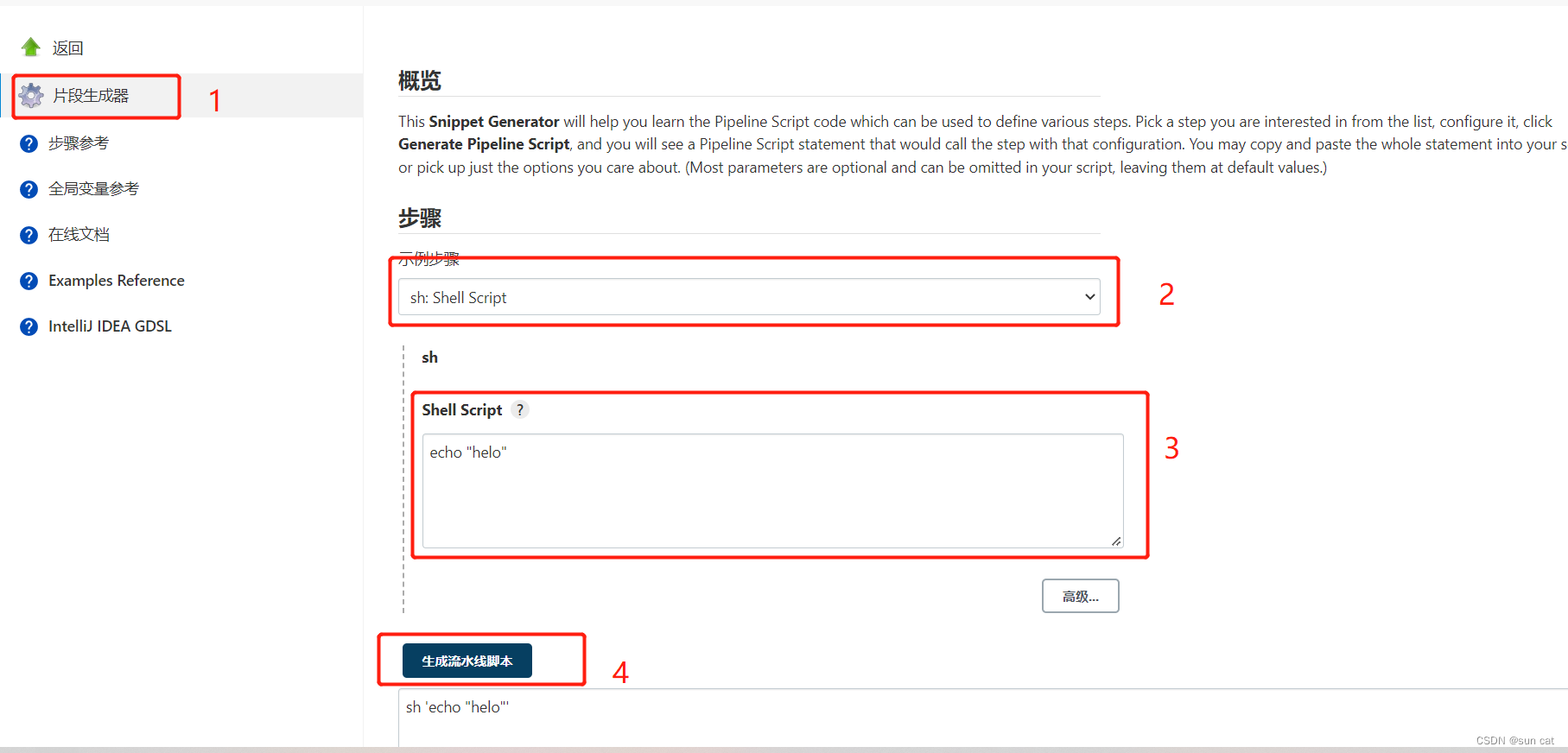
本站原创文章，转载请说明来自《老饼讲解-机器学习》ml.bbbdata.com

一. PCA主成分分析思想介绍

1.1 主成份分析思想

1.2 什么是主成份

二. PCA主成分分析的数学描述

2.1 主成份分析的数学表达

2.2 主成份系数矩阵A的约定

2.3 主成份分析需要输出什么

三. PCA的常用场景

3.1 PCA用于降维

3.2 PCA用于排名

3.3 PCA的实际使用

四. PCA总结与补充

4.1 主成份分析是什么

4.2 特别补充说明

五. 代码实现

5.1 调用sklearn包求解PCA

5.2 自写代码求解PCA

PCA主成份分析常用于降维，是一个基础、知名度极高和常用的方法

本文介绍PCA的原理和本质，并介绍相关使用场景的用法

一. PCA主成分分析思想介绍

本节介绍PCA用于解决什么问题及PCA的思想，初步了解PCA是什么

1.1 主成份分析思想

主成份分析全称为PCA Principle Component Analysis
它的主要功能是去除变量之间的信息冗余，常用于降维和排名等问题



变量间的信息冗余
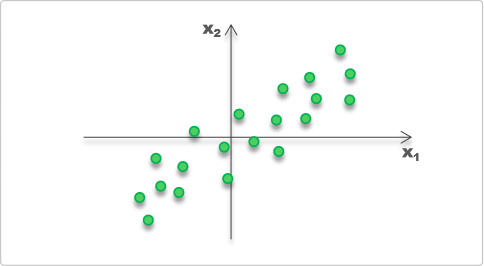
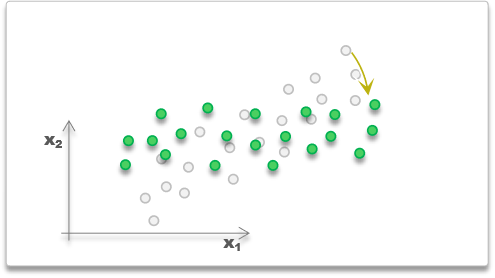
现有样本如下

可以明显看到x1和x2是相关的，它们之间存在信息冗余
例如知道x1很大，那就知道x2也小不到哪去，这就是信息冗余

     主成份分析解决变量相关的思路
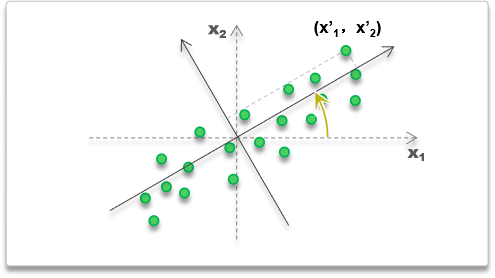
主成份分析是如何解决变量相关的呢？很简单，如下

   PCA的思路就是将坐标轴进行旋转，
让样本在旋转后的坐标轴中各个维度不相关即可

也可以用如下的思路，
将样本进行旋转，使旋转后的样本在各维不相关

1.2 什么是主成份

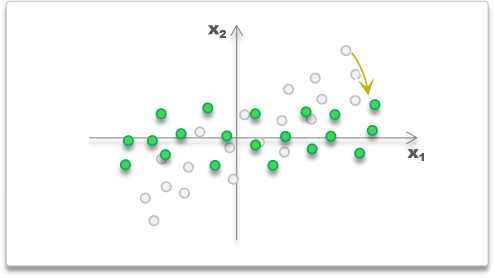
在旋转后，由于各维之间已经没有信息冗余，
每个维度上的方差，就代表该维度携带的信息量

旋转后得到的各个变量是独立地代表样本的某部分信息，
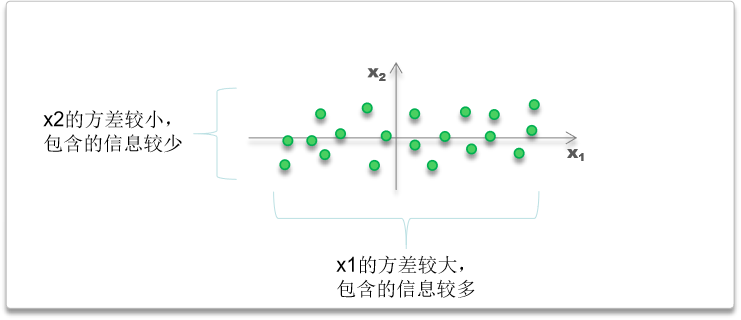
例如，x1的方差为8，x2 的方差为2，
那么可以认为，x1携带了80%的样本信息，x2携带了20%的信息
因此称旋转后得到的各个变量为主成份
并根据方差的大小命名为第一主成份(方差最大)、第二主成份(方差第二大)......
主成份分析即分析样本信息的各个独立部分、主要信息部分

✍️补充
为什么说维度的方差代表包含样本的信息量？
数据点在每个维度的波动幅度有大有小，
波动较小的，则说明各个样本在该维度区别不大，可以忽略
最极致的时候，方差为0，所有样本在该维度完全一样，该维度对样本完全没有区分度
波动较大的，则说明各个样本在该维度差异较大，是区别样本与样本的主要凭据

二. PCA主成分分析的数学描述

本节从数学角度进一步讲解主成份分析PCA是什么

2.1 主成份分析的数学表达

旋转变换在数学中可以用一个标准正交矩阵A表示，
样本原坐标为x,通过A旋转后的坐标就为xA
主成份分析就是找到一个标准正交矩阵A，
将所有样本X进行旋转，使旋转后的样本XA每列不相关
用数学表示，也即找到一个A，使得
$\text{Cov}(XA)=\Lambda$
其中A为标准正交矩阵
Λ代表对角矩阵

2.2 主成份系数矩阵A的约定

可以看到，主成份分析通过A，
实际把原来的n个变量重新线性组合成了新的n个变量
$[x_1,x_2,...,x_n]*\begin{bmatrix} a_{11}&a_{12} & \dots & a_{1n}\\ a_{21}&a_{22} & \dots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}&a_{n2} & \dots & a_{nn} \end{bmatrix}=\left\{\begin{matrix} a_{11}x_1+ a_{21}x_2+...+ a_{n1}x_n=x'_1\\ a_{12}x_1+ a_{22}x_2+...+ a_{n2}x_n=x'_2\\ ...\\ a_{1n}x_1+ a_{2n}x_2+...+ a_{nn}x_n=x'_n \end{matrix}\right.$

其中，A的第 i 列 $[a_{1i},a_{2i},...,a_{ni}]^T$ 就是主成份 $x'_i$ 的系数

为了方便起见，约定A的第i列存放第i个主成份的系数，
即如下

这样x经过A的转换后，得到的变量就依次是第一主成份、第二主成份...

2.3 主成份分析需要输出什么

主成份的主要输出有

👉1.各个主成份的系数矩阵A
👉2.主成份样本数据X'
👉3.各个主成份权重占比Pr

三. PCA的常用场景

本节讲解PCA实际应用中的使用场景和思路

3.1 PCA用于降维

PCA用于降维主要是利用了PCA各维的方差占比代表信息占比的特点
由于每个主成份的方差占比就代表了该主成份所包含的样本信息占比
因此，可以忽略掉一些方差占比小(信息少)的主成份
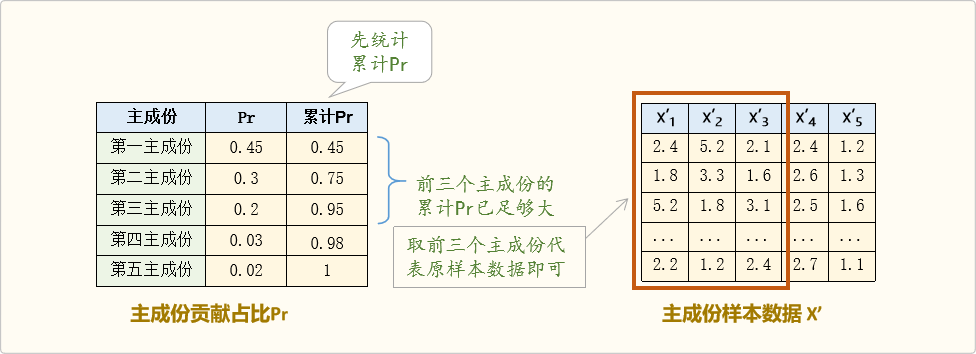
实际操作中，一般先统计累计方差占比，然后按实际情况取足够的占比即可
如下

可以看到，当取前3个主成份时，信息占比已达到95%，
因此，可以忽略其它主成份，只取前3个主成份代表原样本数据即可

3.2 PCA用于排名

PCA应用于排名主要是利用了PCA可以去除冗余信息的特点
例如，学生有语文、数学、物理三科成绩，现要对学生的学习能力进行排名，
由于数学和物理之间存在相关性，
如果用三科成绩总分作为排名，会偏向理科能力强的学生排名更先前
因此，可以先用PCA，将三科成绩转换成新的三个变量(主成份)，
由于这三个变量之间不相关，已经去除信息冗余，
此时用这三个变量的和作为排名，会比简单的成绩总和更为合理
备注：做排名记得每个变量都要与排名正相关哦

3.3 PCA的实际使用

有些模型对变量相关性比较敏感，或者在变量非常多时，容易过拟合，
在实际中，一般是在使用这些模型效果不好时，
就会考虑模型效果不好是否因为变量过多、或变量间的相关性导致的
这时可用PCA先对变量换算成主成份，去除多重共线性，
并把一些贡献率较小的主成份去掉，再把剩余的主成份投入建模
这样做往往就可得到更好一点的效果

✍️备注
PCA的特点主要就两个，
一是去除变量的信息冗余，二是减少变量个数，
只要有这两个需要，都会有PCA的用武之地

四. PCA总结与补充

简单总结和提炼PCA是什么，加固对PCA的特点的记忆

4.1 主成份分析是什么

简单地说，
主成份分析就是输入N个变量，然后将这N个变量重新线性组合成新的N个变量，
新的N个变量之间的互不相关(即相关系数或协方差为0)

它的背后意义就是将样本进行旋转(或将坐标轴进行旋转)

新变量的好处
变量不相关
变量之间相关系数为0，即统计学上不相关，这样变量之间不存在信息冗余
降维作用
新变量可以用每个变量自身的方差，代表该变量的样本信息量，
因此可以忽略掉一些方差小(信息量少)的变量，起到降维的作用
备注：即使降维，并不代表把原来的变量去掉了
例如原本有10个变量，降维时只取3个主成分变量，
但这3个主成份变量仍然是由原来的10个变量线性组合而成的

4.2 特别补充说明

关于样本中心化
上面所说的，都是直接将样本进行旋转

但一般默认，会先将样本中心化，再进行旋转
即X会多一步中心化: $X=X-\overline{X}$
中不中心化无所谓，并不影响PCA的本质和特性，
这里之所以提及，是一般软件里都会进行中心化，
也即最终输出的主成份数据是中心化后的数据 $X'=(X-\overline{X})$
在使用时，记得保持中心化，
例如来了一个 x,将其转换主成份时，需要用 $x'=(x-\overline{X})$ ,而不是直接 $x'=xA$

五. 代码实现

本节编写代码实现PCA的求解，

先调sklearn包求解，再自行写代码求解，并比较结果是否一致

5.1 调用sklearn包求解PCA

下面先通过sklearn包求解PCA中的A，代码如下

# -*- coding: utf-8 -*-
"""
主成份分析求解DEMO(调用sklearn)
本代码来自老饼讲解-机器学习:ml.bbbdata.com
"""
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
# 加载数据
iris   = load_iris()    
X      = iris.data       # 样本X
x_mean = X.mean(axis=0)  # 样本的中心 

# 用PCA对X进行主成份分析
clf = PCA()   # 初始化PCA对象
clf.fit(X)    # 对X进行主成份分析

# 打印结果
print('主成份系数矩阵A:\n A=',clf.components_)
print('主成份方差var:',clf.explained_variance_)
print('主成份贡献占比(方差占比)Pr:',clf.explained_variance_ratio_)

# 获取主成份数据
y = clf.transform(X)                # 通过调用transform方法获取主成份数据  
y2= (X-x_mean)@clf.components_.T    # 通过调用公式计算主成份数据

运行结果如下

主成份系数矩阵A:
 A= [[ 0.36138659  0.65658877 -0.58202985 -0.31548719]
 [-0.08452251  0.73016143  0.59791083  0.3197231 ]
 [ 0.85667061 -0.17337266  0.07623608  0.47983899]
 [ 0.3582892  -0.07548102  0.54583143 -0.75365743]]
主成份方差var: [4.22824171 0.24267075 0.0782095  0.02383509]
主成份贡献占比(方差占比)Pr: [0.92461872 0.05306648 0.01710261 0.00521218]

5.2 自写代码求解PCA

不借助sklearn包，自行编写代码求解PCA的python代码如下

import numpy as np
from sklearn.datasets import load_iris

# 加载数据
iris = load_iris()    
X    = iris.data
x_mean = X.mean(axis=0)  # 样本的中心 

# 通过SVD分解,得到A与XA每列的方差var
U,S,VT = np.linalg.svd((X-x_mean)/np.sqrt(X.shape[0]-1)) # 注意，numpy的SVD分解出的是US(VT)
A      = VT.T                                            # 主成份系数矩阵A
var    = S*S                                             # 方差                                    
pr     = var/var.sum()                                   # 方差占比

#打印结果
print('主成份系数矩阵A:\n A=',A)
print('主成份方差var:',var)
print('主成份贡献占比(方差占比)Pr:',pr)

# 获取主成份数据
y= (X-x_mean)@A                                          # 通过调用公式计算主成份数据

运行结果如下

主成份系数矩阵A:
 A= [[ 0.36138659 -0.65658877  0.58202985  0.31548719]
 [-0.08452251 -0.73016143 -0.59791083 -0.3197231 ]
 [ 0.85667061  0.17337266 -0.07623608 -0.47983899]
 [ 0.3582892   0.07548102 -0.54583143  0.75365743]]
主成份方差var: [4.22824171 0.24267075 0.0782095  0.02383509]
主成份贡献占比(方差占比)Pr: [0.92461872 0.05306648 0.01710261 0.00521218]