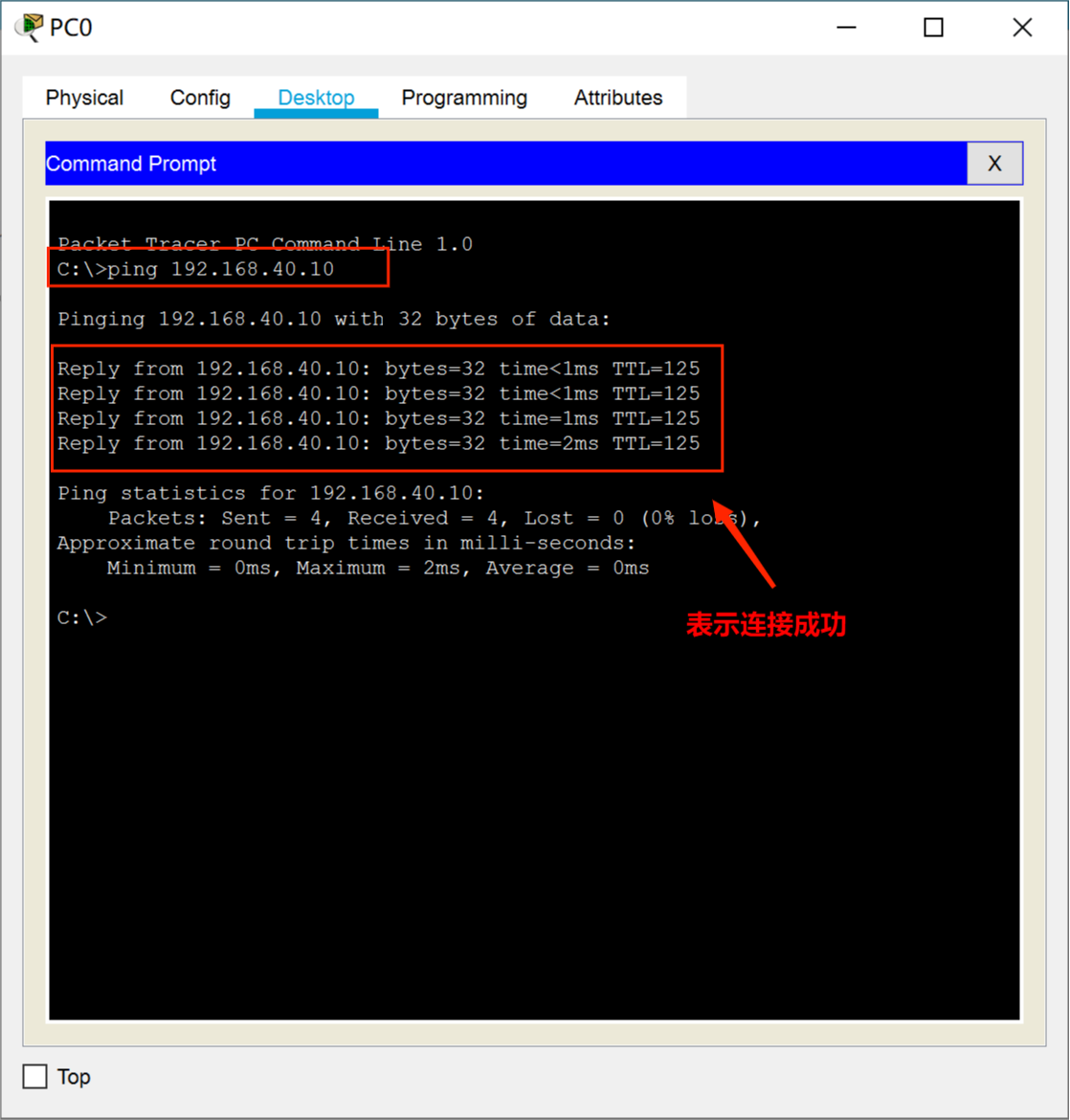
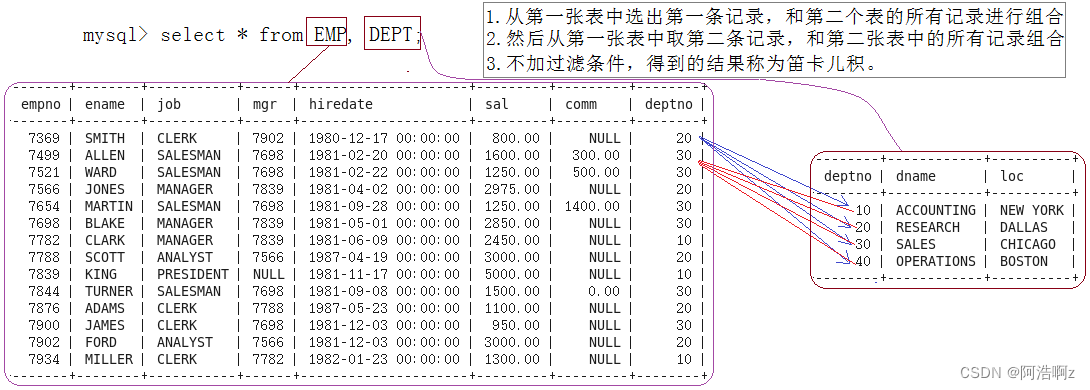
输入样例：

5
3
14
15
24
1

输出样例：

1
2
1
3
0

思路分析：

首先搭每个金字塔所需的扑克牌数并不会由n决定，所以我首先想到打表。抱着信心尝试一番之后

既然文件太大提交不了，那我们就放弃:，怎么可能，下面我们来简单的计算一波，打表时间复杂度O(n),二分时间复杂度O(log n),所以打表+二分，时间复杂度OK。
所以这一题的思路就是：把打表程序放在主程序里，用二分查找搭成最大金字塔所需扑克牌数量，
再通过递归解决。
既然要打表 (其实叫预处理) 那就先分析一下金字塔的规律 (如下图) ：
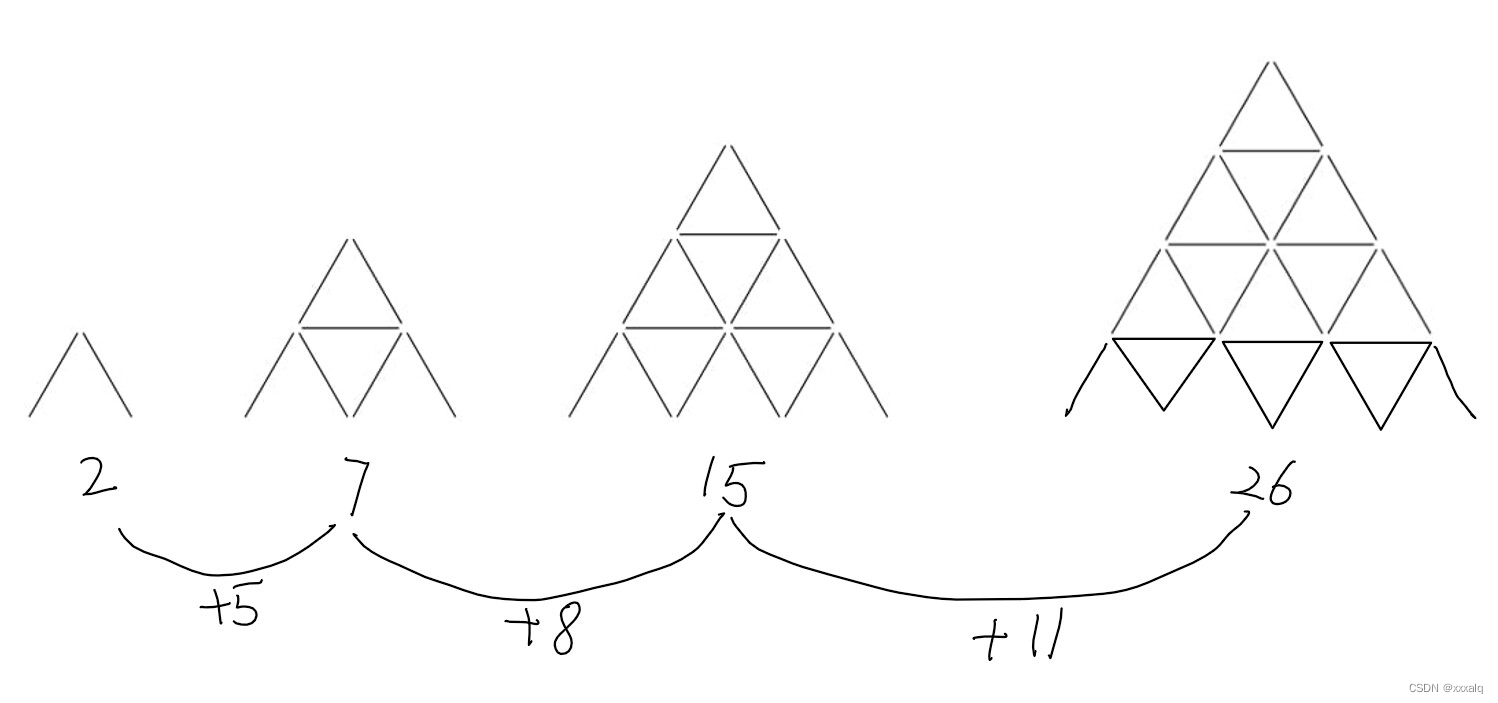总结规律：每次差增加3
接着用二分查找出离n最近的金字塔，然后减去那个数在递归查找剩下的，知道小于2为止，因为最小的金字塔要2张扑克牌。

代码：

#include<iostream>
using namespace std;
int a[25850];//预处理数组 
int t,n;//由题意 
int ans=0;//记录答案 
void dg(int x){
	if(x<2){
		return;
	}//递归终止条件 
	int l=0,r=25850,mid;//r=25850是打表测出来的，在1e9内有25820种不同的金字塔结果，开大一点到25850 
	while(l<r){//二分 
		mid=(l+r+1)/2;
		if(a[mid]>x){
			r=mid-1;
		}else{
			l=mid;
		}
	}//找不大于x的最大值下标 
	ans+=1;//答案加一 
	dg(x-a[l]);//剩下的继续找 
	return;
}
int main(){
	int cnt=0/*所需扑克牌张数*/,tmp=2/*差值*/,idx=-1;//a数组下标 
	while(cnt<=1000000000){ 
		cnt+=tmp;
		tmp+=3;//差值加3 
		idx+=1;//下标加一 
		a[idx]=cnt;
	}//在输入前预处理(打表) 
	cin>>t;
	while(t--){//t次询问 
		ans=0;//答案初始化 
		cin>>n;
		dg(n);//递归调用 
		cout<<ans<<endl;
	}
	return 0;
}

下一篇：可可口乐