系列文章目录

---

前言

一、DOE五步法

1. 拟合选定模型
2. 进行残差诊断
3. 模型是否需要改进？
4. 对选定模型进行分析解释
5. 目标是否已达到>进行验证试验

二、分析要点

1.ANOVA表的分析

1. 主效应和2因子交互作用中至少一项P<0.05，意味着模型总体来说是有效的；如果P>0.05，意味着模型无效，整个实验没有任何意义的结果；
2. 看ANOVA表中的失拟现象，如果失拟P>0.05，意味着模型没有失拟现象；若P<0.05，意味着模型漏掉了重要的项(例如高阶交互作用项等)，本项计算的依据是：最初是以重复实验间的差异作为实验误差的估计，将缺失的项(例如高次项、高阶交互作用等)所造成的误差平方和与之相比，经过F检验即可判明，以后，将判明为不显著的各项都归并为随机误差项，重新计算失拟项是否显著；
3. 看ANOVA表中的弯曲项，如果弯曲项P>0.05，意味着模型没有弯曲现象；若P<0.05，说明数据呈现弯曲，而模型中并没有平方项，应该补上；本项计算依据是：最初是以重复实验的差异及失拟项的误差作为实验误差的估计，将高低水平的两个数据连同中心点的实验数据，构成自变量的三个不同的观测值，扣除线性项后可得二次项的平方和，将二次项误差的均方与实验误差的均方和相比较，经过F检验即可判明是否呈现弯曲；

模型无效的原因：

• 实验误差较大；
• 实验设计中漏掉了重要因子；
• 模型本身有问题，例如有失拟或数据本身有较强的弯曲；

2.分析评估回归的总效果

1. 两个确定系数R平方及Radj的平方：拟合的总效果可以用确定系数R平方(也称为多元全相关系数)及调整的确定系数(也称为调整的多元全相关系数)
   
   式中，n为观测值总个数，p为回归方程中的总项数(包括常数项)。即Radj的平方（R-sq调整）是扣除了回归方程中所受到的包含项数的影响的相关系数，因而可以更准确的反映模型的好坏。因为Radj平方总比R平方小一些，因此在实际应用中，我们通过二者的接近程度判断；二者只差越小说明模型越好。我们常常比较包含所有自变量有关的"全模型"与删除所有影响不显著的项后的"缩减模型"，如果将影响不显著的项删去后二者更接近，则说明删去的这些项使得模型得到了改进；
2. 对S值和S平方的分析：所有的观测值与理论值之间可以有误差，但总是假定这个误差应该服从以0为均值以Sigma平方为方差的正态分布。在ANOVA表中，对于残差误差中的平均离差平方和(adj MS)数值则恰好是Sigma平方的无偏估计量，我们将其记为均方误MSE，而此量与其平方根S一并输出，可以认为S值是Sigma的估计。比较两个模型的优劣最关键的指标就可以选择S或S平方。哪个模型使之最小，哪个模型就最好；
3. 对预测结果的整体估计：如果某个点在模型中起特别重要的作用，此点可能为异常点，或杠杆点，此点对方程的影响较大，我们特别要警惕得到的方程是否为受个别点影响而形成的"虚假"回归方程，这种方程从表面上看可能拟合的不错，但是做预测效果并不好。为了鉴别回归方程是否为"虚假"方程，我们引入两个统计量PRESS和R-sq预测。(a)PRESS是预测的误差平方和，它与原来的SSE很相似，但它参与求和的各项"残差"已与原来不同。这里对于第i个观测值的预测值所使用的回归方程不是用全部观测值来获得的，而是将第i个观测值删除后拟合的回归方程，然后求出其残差，即轮番删除一个，计算一个残差，最后把这些残差求出平方和，这就是PRESS;用全部观测值来获得的回归方程，当然它肯定会受到第i个观测值的影响，会使回归方程有向此实际观测值"靠拢"的效果，因而残差会小些；删除第i个观测值后则会"客观"很多，它避免了第i个观测值本身的影响；(b)另一个统计量是"预测的R平方"
   
   是使用全部数据拟合的回归方程后得到的残差平方和，将SSE换成PRESS，则可以得到预测的R平方，简记R-sq预测。此值通常会比R平方及(R-sq)小一些，如果小的不多，则表明数据点中有特殊地位的点不多，或它们的影响不大(保留第i个观测值与删除第i个观测值对回归方程几乎没什么影响)，将来用回归方程做预测结果也比较可信。

3.分析评估各项效应的显著性

为了把所有的效应不显著的全部删除，就要对各项效应的显著性进行逐个检验。在minitab结果输出的最开始部分就有回归系数的统计检验，这里列出了各项的效应，回归系数的标准误及检验结果。这是对各项的分别的检验，可以在修改模型时删除不显著的。要注意的是：如果一个高阶项时显著的，则此高阶项所包含的低阶项也要包含进去。

三、图像解释

1.Pareto图

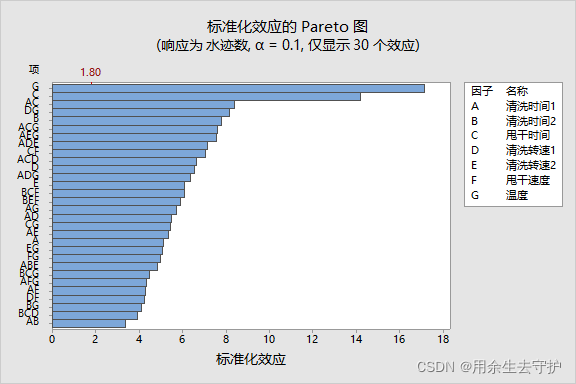
Pareto效应图是将各效应的t检验所获得的T值的绝对值作为纵坐标，按照绝对值的大小排列起来，根据选定的显著性水平Alpha，给出t值的临界值(注意按t的双侧拒绝域)绝对值超过临界值的效应被选中；用Pareto效应图来判断因子效应的显著性是非常直观的，但它有个缺点，就是进行各效应的t检验时，首先要用S平方估计出Sigma平方,而通常S平方并不一定可靠，因此在数据与模型拟合不好的情况下，Pareto效应图不一定准确；

2.正态效应图

远离直线为显著因子，直线附近或直线上为不显著因子，右面为正效应，左面为负效应；

我们将各因子的效应按由小到大(正负号考虑在内)排成序列，将这些效应点标在正态概率图上，就是正态效应图。其原理：可以假定大多数因子中只会有少数因子效应是显著的，即遵循"效应稀疏原则"，因此，当挑选位于中间的一些效应的点群拟合一条直线，它们的效应应该是最不显著的，效应应该服从正态分布，点全在直线上；某些效应确实非零时，相应的估计效应绝对值应会偏大，即远离直线。对于正效应，估计的效应将落在直线的右下方，对于负效应，估计的效应应落在直线的左上方。

3.半正态效应图

半正态效应图与正态效应图完全相同，只是所有效应只考虑绝对值；

4.残差图

DOE分析"五步法"中第二步就是进行残差诊断。这一步主要目的是基于残差的状况来诊断模型是否与数据拟合的很好。单纯从ANOVA表及回归系数的估计与检验系数两方面结果来分析整个结果是远远不完整的。为了弥补结果不足，我们要进行残差诊断。我们定义的残差是观测到的响应变量数据与代入回归模型后的预测值之差，因此应该满足：residual~N(0,Sigma平方)。如果满足则模型正确；否则要进行修改；进行的残差诊断比一般回归分析中的残差诊断多了一个有利条件，这就是中心点重复实验提供的残差是随机误差的正常状况，比较时可以拿中心点的残差作为比较的基准；

• 在"四合一图"，观察残差对于以观测值顺序为横轴的散点图，重点考察此散点图中的各点是否随机地在水平轴上下无规则地波动；
• 在"四合一图"，观察残差对于以响应变量拟合预测值为横轴的散点图，重点考察此散点图中残差是否保持等方差性，即是否有"漏斗形",“喇叭形”。
• 在"四合一图"，正态概率图，观察残差的正态性检验图，看残差是否服从正态分布；
• 观察残差对于各自变量为横轴的散点图，考察散点图是否有弯曲趋势；

异常情况：

• 第一种最常见的残差图不正常出现在残差对响应变量拟合值的图中，残差未保持等方差性，散点有明显的"漏斗形",“喇叭形”，这说明对响应变量y做某种变换后会使得模型拟合更好；例如
  
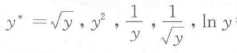
  等作为新响应变量，可能会好很多；
• 第二种最常见的残差图不正常情况出现在残差对自变量的散点图中，残差虽然保持等方差，但散点明显有U型或倒U型弯曲，这说明对响应变量y而言，对该自变量x仅取线性已经不够了，应增加x的平方项或立方项，将会使模型拟合更好；

5.Box-Cox变换结果图

我们在最开始操作分析因子设计时，曾在"存储"项中除了拟合值，残差，标准化残差外，还要求存储设计矩阵，它的具体存储位置我们可以打开显示设计

%boxcoxdoe C6 M1 32 C21-C60

提示：minitab需要安装宏库！！

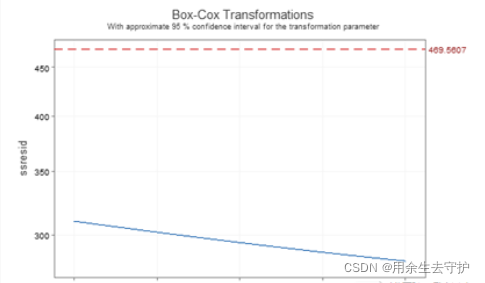
这里的横轴是Box-Cox变换的方幂λ，纵轴是按此λ进行响应变量变换后所形成的残差平方和，曲线用蓝色实线显示。图形最上方的红色虚线表示符合方差齐性要求的残差平方和上限，如果残差平方和蓝色曲线落在红色虚线下方，则表示用此λ值进行变换已经可以使残差达到齐性。而当λ＝1时，表示不必进行变换。因此分析此图关键是看在λ＝1处，残差平方和蓝色曲线是否落在红色虚线下方。如果残差平方和蓝色曲线确实落在红色虚线下方，则不必对y进行变换；反之，则需要进行变换，而对于λ的选择则只要寻求蓝色曲线的最低点附近的λ即可。将响应变量进行变换后，一切都要从头开始，重新拟合模型。
本案例在λ＝1处，残差平方和蓝色曲线确实落在红色虚线下方，说明方差齐性要求是满足的，不必再对y进行变换。

四、判断模型是否需要改进

DOE分析五步法中的第三步是判断模型是否需要改进

1. 残差对拟合预测值的诊断图中，是否有不齐性或弯曲；如果有，我们要对响应变量y做变换；
2. 残差对自变量的诊断图是否有弯曲，如果有，要考虑增加x的平方项或立方项会使模型拟合更好，此时要修改模型(例如进行响应曲面设计，重新安排或增加实验，重新拟合)；
3. 删除不显著因子，重新拟合；

五、删减模型判断

删除不显著因子后，R-sq通常会有微小的降低，但关键是看R-sq调整是否有所提高，若二者接近，则回归效果更好；

1. 再次进行残差诊断：此时残差诊断的目的与前面的不同，前面诊断着重考虑模型是否与数据拟合合适，如何修改以求拟合的更好，此时是在肯定模型的前提下判断数据中是否有个别点存在异常；检验方法是将分析正规残差换为分析标准残差，标准化残差在一般教材中称为t化残差，它不是简单的把残差减均值并处以残差的标准差，它还要考虑到自变量观测值到自变量平均值之间的距离等因素。标准化后的残差可以近似看成相互独立的服从标准化正态分布的随机变量，因此，标准化残差的绝对值一般不应超过2(标准正态分布落在正负2之外的概率大约为5%)，这个可以用来检查单个观测值是否有异常（这种异常不是指观测值的大小，而是是否偏离模型）；也可以将正规残差换为删后残差，删后残差是指全部数据中删除本数据而保留别的数据再进行回归时对本观测值所得到的残差，删后残差的平方和就是PRESS。
2. 如果在实际问题中遇到异常点，或强影响点，要考虑它对估计和拟合的种种影响，解决方法一般有两种：一是观察删除此点后方程的变化，二是采用一些不太受这种点影响的估计方法，主要有R方法(数据的秩数据)和M方法(休伯提出的极大似然法)。具体做法为：打开原数据文件，可以看到你和最后选定的模型后所形成的标准化残差列，仔细查看如果全部数值的绝对值都不超过2，则可认为无异常点，如果有个别数据超过2，可认为此点为异常点；如果绝对值超过2的数不超过总体的5%,则异常不严重；

6.主效应图

越陡说明越显著

立方图通常不用，除非交互作用太严重，简单效应找不到最优点时使用；

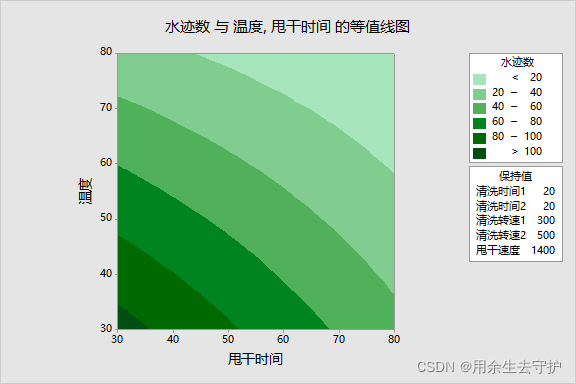
7.等值线&响应曲面图

可以观察响应变量是如何受所选中的主因子和交互作用影响的。

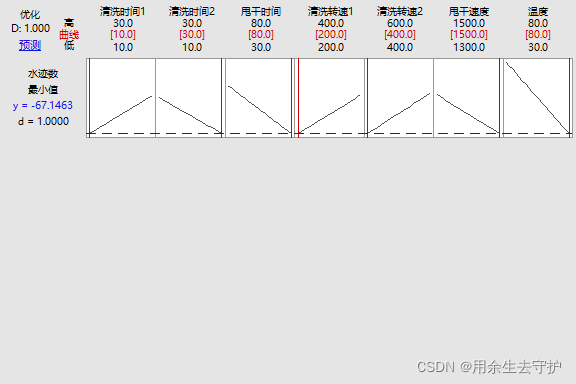
8.响应优化

---

总结

分享：
我觉得艺术、诗歌和宗教的存在，其目的是辅助我们恢复新鲜的视觉，富于情感的吸引力和一种更健全的人生意义。