简介

pgvector 库是一种用于计算向量距离的库，它的核心是提供了聚类索引，棸类索引使用的算法是 kmeans++（相对于 kmeans 最主要的区别是初始化起点的位置）。

pgvector 索引的存储结构

meta page → list page → entry page

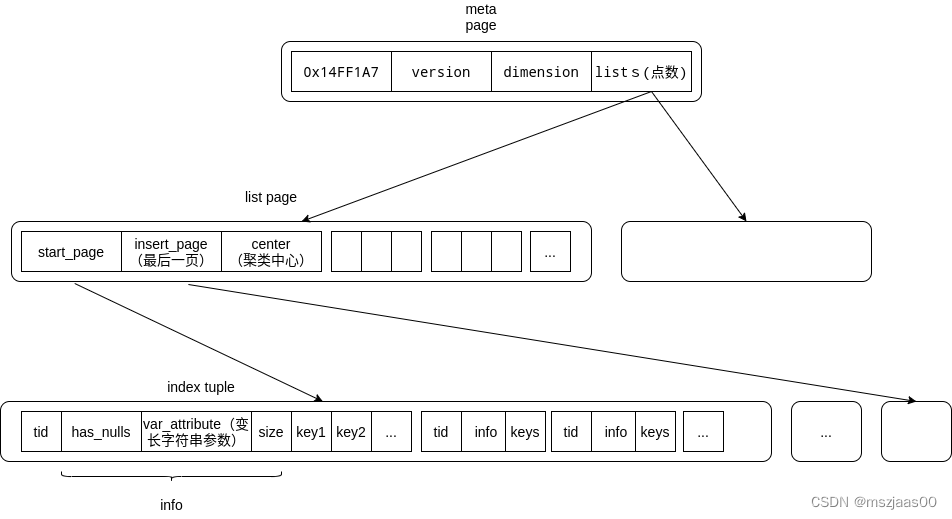
insert page 是最后一页，当发生过 vacuum 后它会指向第一个回收了 tuple 的页，下一次插入 indextuple 从这个页开始

对pgvector 来说，keys 是点的向量值

索引创建过程

用户创建时指定计算距离的方法（ivfflat 的参数）与棸类中心的数量(lists)

CREATE INDEX ON t USING ivfflat (val) WITH (lists = 1);

build 过程： 计算中心节点－》创建meta/list页－》填充entry页

计算中心节点

1、初始化中心节点

使用 kmeans++ 算法：假设要聚ｎ类

• 采集一定的样本点（50×ｎ个），
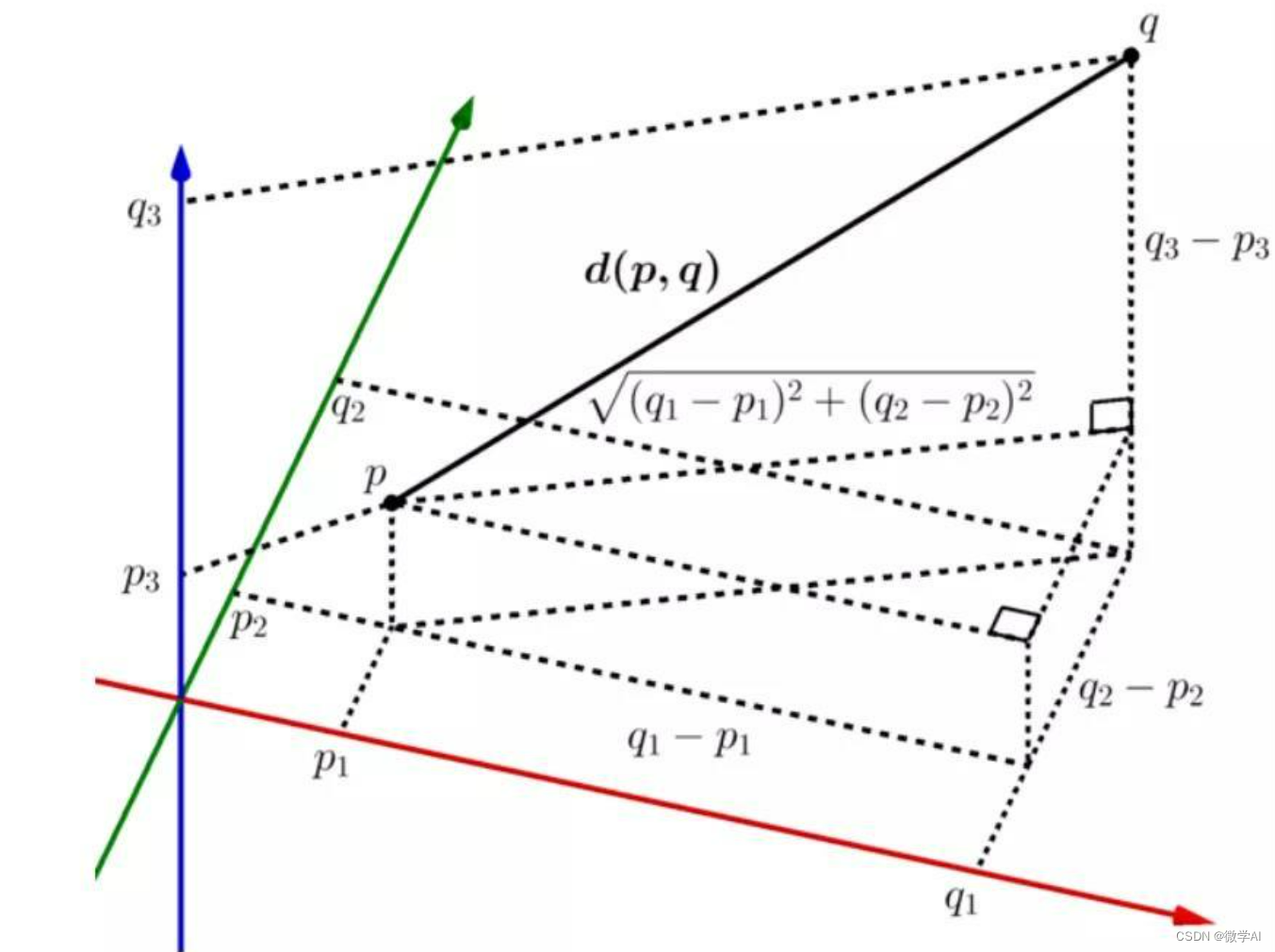
• 随机选１个点作启动点，计算每个点到这个中心点的距离
• 以每个点到这个中心点的距离为权重，重新筛选出一个点作为新的初始中心（认为离最近棸类中心最远的点，最可能成为棸类中心，InitCenters），总共选出ｎ个新初始中心

２、计算每个中心点相对最近中心点的距离，检查是否所有其它点到中心点ｘ的距离小于中心点ｘ与最近中心ｙ之间的距离

３、对大于中心点间距离的点，重新找到离它最近的中心点，加入对应的簇

４、重新计算每个簇的中心点（计算所有簇内点每个维度的平均值作为第一维度的值，并对这个算出来的点的所有维度做统一正则化）

５、计算新中心与老中心的距离，把这个距离更新到每个点与中心的距离的上下界上（因为d(x,old) c- d(old,new) < d(x,new) < d(x,old) + d(old,new) ）

6、循环至棸类中心不再变

填充entry页

１、起并行 worker 去扫描每个 tuple 做棸类（AssignTuples）

２、由 leader 去合并每个 worker 的 tap，合并的过程实际是对每个点属于的簇号作排序（tuplesort_performsort），未对簇内的 vector 做排序

３、为每个簇（list）插入实际的 indextuple（InsertTuples），index key 是 点向量值

worker的并行度

worker的并行度取决于用户对源表 set 的 rel_parallel_workers，用户未指定时，并行度为 log3(表的页数)，并且要满足每个 worker 可以分到 32ｍ 内存，用户未配置的情况下，为worker分配的总默认内存为64m（默认无法并行worker，因为master + worker至少要64m）。

sort 的执行

索引的scan

１、找每个聚簇中心，计算中心与目标点的距离，利用堆排序找出最近的 topN 中心，Ｎ取决于用户设置的ivfflat.probes。（GetScanLists）

２、去中心点簇对应的entry页，一页页找取点算距离，最后sort 一下（GetScanItems）

３、后面就可以一条条tuplesort_gettupleslot了（index 的数据不会删除，依赖于 postgresql 的 HOT 机制，真正删除发生在 vacuum 中）

vacuum

vacuum 时遍历 list/entry 页，看是否在 vacuum 普通表时已经 vacuum 过 tuple（lazy_record_dead_tuple），如果删除过，则收集这个 indextuple，最后执行页的vacuum并记 xlog，并更新下一个 insert page number（相当于回收tuple 位置）

这里有个细节，第一次 delete 一页的 tuple 时，要记一个 copy（GenericXLogRegisterBuffer），每次记录delete tuple位置时，要从这个 copy 中去记录 delete 的位置，最后一并执行 delete（pg给的接口是这样的）

cost 计算

page cost

计算随机访问 index page 的 cost：根据扫描的输出的点数（ivfflat.probes），估算扫描的 tuple 数，再根据 index 过滤条件，判断扫描出的 index tuple 数，进而算出扫描 index 页数，从而得到 random 访问的 index page 的 cost

如果是 join 的 inner 部分，总共访问 index page cost 要乘上 loop_count，然后再考虑 cache 带来的 cost 消除，这部分公式有点复杂，可以不看

$$|page\_fetch|=\{\begin{array}{ll}min(\frac{2\ast page\ast tuple\ast frac}{2\ast page+tuple\ast frac},page)& page\le tuple\\ 2\ast page\ast tuple\ast frac/(2\ast page+tuple\ast frac)& page>tuple,tuple\ast frac<=\frac{2\ast page\ast buf}{2\ast page-buf}\\ buf+\frac{(tuple\ast frac-\frac{2\ast page\ast buf}{2\ast page-buf})\ast (page-buf)}{page}& page>tuple,tuple\ast frac>\frac{2\ast page\ast buf}{2\ast page-buf}\end{array}$$

index 默认是 random 访问的，random 访问的代价是 sequence 访问的四倍，而实际实现的访问是 seq 访问的，所以减去 seq 与 random 访问的差值。

这个过程中，如果点 vector 的维度很大，导致用 toast 类型来存 index（现象是算的 index page 访问数比 index 实际 page 数高，说明 index 是 toast 存储，因为 toast 存储不记录为 index 页），这个时候，要记得减去 toast 页算出的随机访问 cost。

cpu cost

• where 条件本身 cost，order by 条件本身 cost
• cpu_index_tuple_cost + cpu_operator_cost × (where 条件数 + order by 数) * tuple 数