爬楼梯—递归分析

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？ 注意：给定 n 是一个正整数。

示例 1：
输入： 1
输出： 1
解释： 有一种方法可以爬到楼顶。
方法1：1 阶

示例 2：
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
方法1：1 阶 + 1 阶
方法2：2 阶

---

继续向后分析，我们会得到：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
方法1：1 阶 + 1 阶 + 1 阶
方法2：1 阶 + 2 阶
方法3：2 阶 + zh1 阶

输入： 4
输出： 5
解释： 有5种方法可以爬到楼顶。
方法1：1 阶 + 1 阶 + 1 阶 + 1 阶
方法2：1 阶 + 1 阶 + 2 阶
方法3：1 阶 + 2 阶 + 1 阶
方法4：2 阶 + 1 阶 + 1 阶
方法5：2 阶 + 2 阶

输入： 5
输出： 8
解释： 有5种方法可以爬到楼顶。
方法1：1 阶 + 1 阶 + 1 阶 + 1 阶 + 1 阶
方法2：1 阶 + 1 阶 + 1 阶 + 2 阶
方法3：1 阶 + 1 阶 + 2 阶 + 1 阶
方法4：1 阶 + 2 阶 + 1 阶 + 1 阶
方法5：1 阶 + 2 阶 + 2 阶
方法6：2 阶 + 1 阶 + 1 阶 + 1 阶
方法7：2 阶 + 1 阶 + 2 阶
方法8：2 阶 + 2阶 + 1 阶

总结一下上述的内容：

当1层楼梯时，有1种方法，表示为：f(1) = 1
当2层楼梯时，有2种方法，表示为：f(2) = 2
当3层楼梯时，有3种方法，表示为：f(3) = f(2) + f(1) = 3
当4层楼梯时，有5种方法，表示为：f(4) = f(3) + f(2) = 5
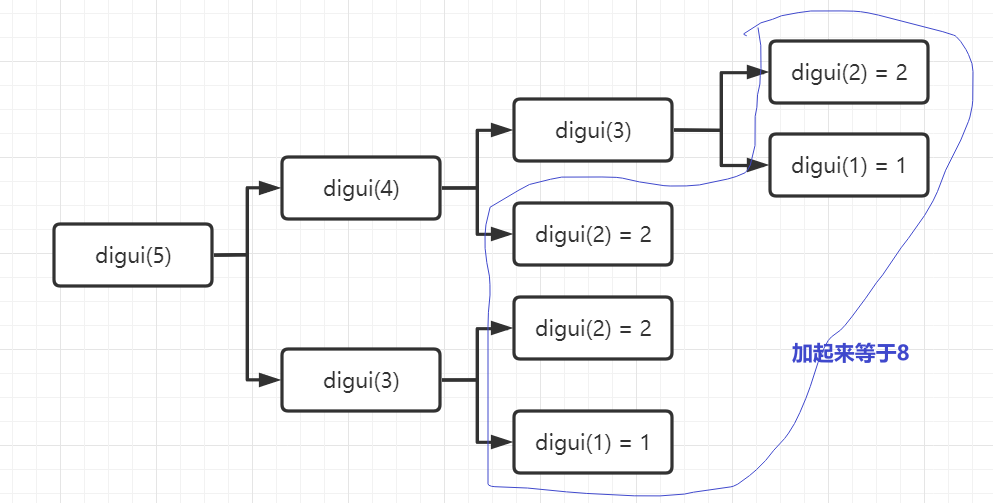
当5层楼梯时，有8种方法，表示为：f(5) = f(4) + f(3) = 8
…（以此类推）
当n层楼梯时，有f(n)种方法，表示为：f(n) = f(n-1) + f(n-2) = ?

python代码如下：

def digui(n):
    if n == 1:
        return 1
    if n == 2:
        return 2
    return digui(n - 1) + digui(n - 2)

print(digui(5))

运行结果：

8

流程图思路分析：