👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——线性回归的简洁实现
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
softmax回归
- 分类问题
- 网络架构
- 全连接层的参数开销
- softmax运算
- 小批量样本的矢量化
回归可以用来预测多少的问题,比如房屋被售出价格。而除了预测,我们也对分类问题感兴趣,不是问“多少”,而是问“哪一个”。如:“某个邮件是否是垃圾邮件?图像描绘的是什么动物?某人接下来最可能看哪部电影?”
分类问题
以图像分类为例,每次输入一个2×2的灰度图像,可以用一个标量表示每个像素值,每个图像对应四个特征x1、x2、x3、x4。假设每个图像属于类别“猫”“鸡”和“狗”中的一个。
接下来要选择如何表示标签,最直接的想法是选择y∈{1,2,3}分别代表{狗,猫,鸡}。
如果类别间有一些自然顺序,比如我们要试图预测{婴儿,儿童,青少年,青年人,中年人,老年人},那么该问题就会转变为回归问题。但一般的分类问题和类别之间的自然顺序是无关的。
独热编码
独热编码是一个向量,它的分量与类别是一样多的。类别对应的分量设置为1,其它所有分量设置为0,如:
y∈{(1,0,0),(0,1,0),(0,0,1)}分别代表三类动物。
网络架构
要解决线性模型的分类问题,需要设置和输出一样多的仿射函数,在上面的问题中,我们有4个特征和3个可能的输出类别,所以我们需要用12个标量来表示权重,3个标量来表示偏置(带下标的b):
o
1
=
x
1
w
11
+
x
2
w
12
+
x
3
w
13
+
x
4
w
14
+
b
1
o
2
=
x
2
w
21
+
x
2
w
22
+
x
3
w
23
+
x
4
w
24
+
b
2
o
1
=
x
1
w
31
+
x
2
w
32
+
x
3
w
33
+
x
4
w
34
+
b
3
o_1=x_1w_{11}+x_2w_{12}+x_3w_{13}+x_4w_{14}+b_1\\ o_2=x_2w_{21}+x_2w_{22}+x_3w_{23}+x_4w_{24}+b_2\\ o_1=x_1w_{31}+x_2w_{32}+x_3w_{33}+x_4w_{34}+b_3
o1=x1w11+x2w12+x3w13+x4w14+b1o2=x2w21+x2w22+x3w23+x4w24+b2o1=x1w31+x2w32+x3w33+x4w34+b3
其中o表示未规范化的预测。
我们可以用神经网络图来描述这个计算过程,显然softmax回归也是个单层神经网络。由于输出取决于所有的输入,所以softmax回归的输出层也是全连接层
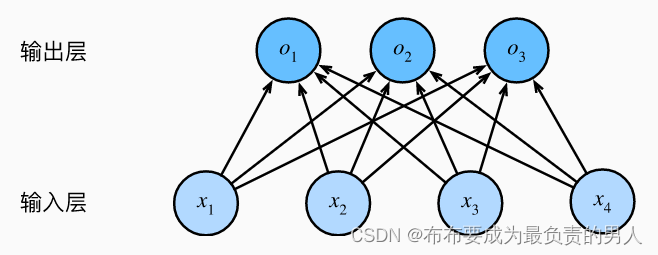
可以用o=Wx+b来表示模型。
全连接层的参数开销
全连接层无处不在,对于任何具有d个输入和q个输出的全连接层,参数开销为:
O
(
d
q
)
O(dq)
O(dq)
这个数字还是太大了,但将d个输入转换为q个输出的成本可以减少到:
O
(
d
q
n
)
O(\frac{dq}{n})
O(ndq)
超参数n可以由我们灵活指定。
softmax运算
现在我们将优化参数以最大化观测数据的概率。为了得到预测结果,我们设置一个阈值,如选择具有最大概率的标签。
我们希望模型输出三个类的概率,然后选用最大输出值来作为我们的预测。
但我们不能将未规范化的预测o直接视作我们感兴趣的输出。因为将线性层的输出直接视为概率时会存在一些问题:
1、我们没有限制这些输出数字的总和为1。
2、根据输入的不同,它们可以为负值,违背了概率基本公理。
要将输出视为概率,必须保证在任何数据上的输出都是非负的且总和为1。此外,需要训练一个目标函数,来激励模型精准的估计概率。例如,在分类器输出0.5的所有样本中,我们希望这些样本是刚好有一半实际上属于预测的类别。这个属性叫做校准。
而softmax函数能够将未规范化的预测变换为非负数并且总和为1,同时让模型保持可导的性质。为了完成这一目标,我们首先对每个未规范化的预测求幂,这样可以确保输出非负。为了确保最终输出的概率值总和为1,我们让每个求幂后的结果除以它们的总和:
y
^
=
s
o
f
t
m
a
x
(
o
)
,其中
y
^
j
=
e
x
p
(
o
j
)
∑
k
e
x
p
(
o
k
)
\hat{y}=softmax(o),其中\hat{y}_j=\frac{exp(o_j)}{\sum_kexp(o_k)}
y^=softmax(o),其中y^j=∑kexp(ok)exp(oj)
这里,对于所有的j,总有:
0
≤
y
^
j
≤
1
0≤\hat{y}_j≤1
0≤y^j≤1
因此,y hat可以视为一个正确的概率分布。
softmax运算不会改变未规范化的预测o之间的大小次序,只会确定分配给每个类别的概率。因此,在预测过程中,我们可以用下式来选择最有可能的类别:
a
r
g
m
a
x
j
y
^
j
=
a
r
g
m
a
x
j
o
j
argmax_j\hat{y}_j=argmax_jo_j
argmaxjy^j=argmaxjoj
尽管softmax是一个非线性函数,但softmax回归的输出仍然由输入特征的仿射变换决定。因此,softmax回归是一个线性模型。
小批量样本的矢量化
为了提高计算效率并且充分利用GPU,我们通常会对小批量样本的数据执行矢量计算。假设我们读取了一个批量的样本X,其中特征维度(输入数量)为d,批量大小为n。此外,假设我们在输出中有q个类别。那么:
小批量样本的特征为
X
∈
R
n
×
d
权重为
W
∈
R
d
×
q
偏置为
b
∈
R
1
×
q
小批量样本的特征为X∈R^{n×d}\\ 权重为W∈R^{d×q}\\ 偏置为b∈R^{1×q}
小批量样本的特征为X∈Rn×d权重为W∈Rd×q偏置为b∈R1×q
softmax回归的矢量计算表达式为:
O
=
X
W
+
b
Y
^
=
s
o
f
t
m
a
x
(
O
)
O=XW+b\\ \hat{Y}=softmax(O)
O=XW+bY^=softmax(O)
小批量样本的矢量化加快了X和W的矩阵-向量乘法。
由于X中的每一行代表一个数据样本,那么softmax运算可以按行执行:对于O的每一行,我们先对所有项进行幂运算,然后通过求和来对他们进行标准化。(XW+b的求和会使用广播机制,小批量的未规范化预测和输出概率都是n×q的矩阵)。

![C国演义 [第十一章]](https://img-blog.csdnimg.cn/abf028a942814cc6a9e041e6b8314b86.png)