有向图的强联通分量(SCC)Tarjan算法
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
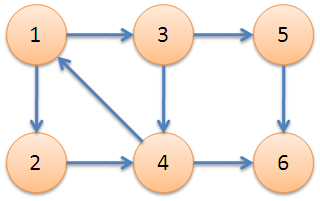
DFS生成树:
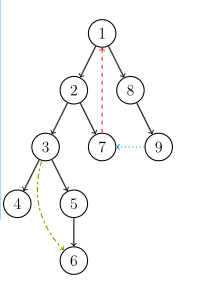
- 树边(tree edge):示意图中以黑色边表示,每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
- 反祖边(back edge):示意图中以红色边表示(即7->1 ),也被叫做回边,即指向祖先结点的边。
- 横叉边(cross edge):示意图中以蓝色边表示(即9->7 ),它主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先。
- 前向边(forward edge):示意图中以绿色边表示(即3->6 ),它是在搜索的时候遇到子树中的结点的时候形成的。
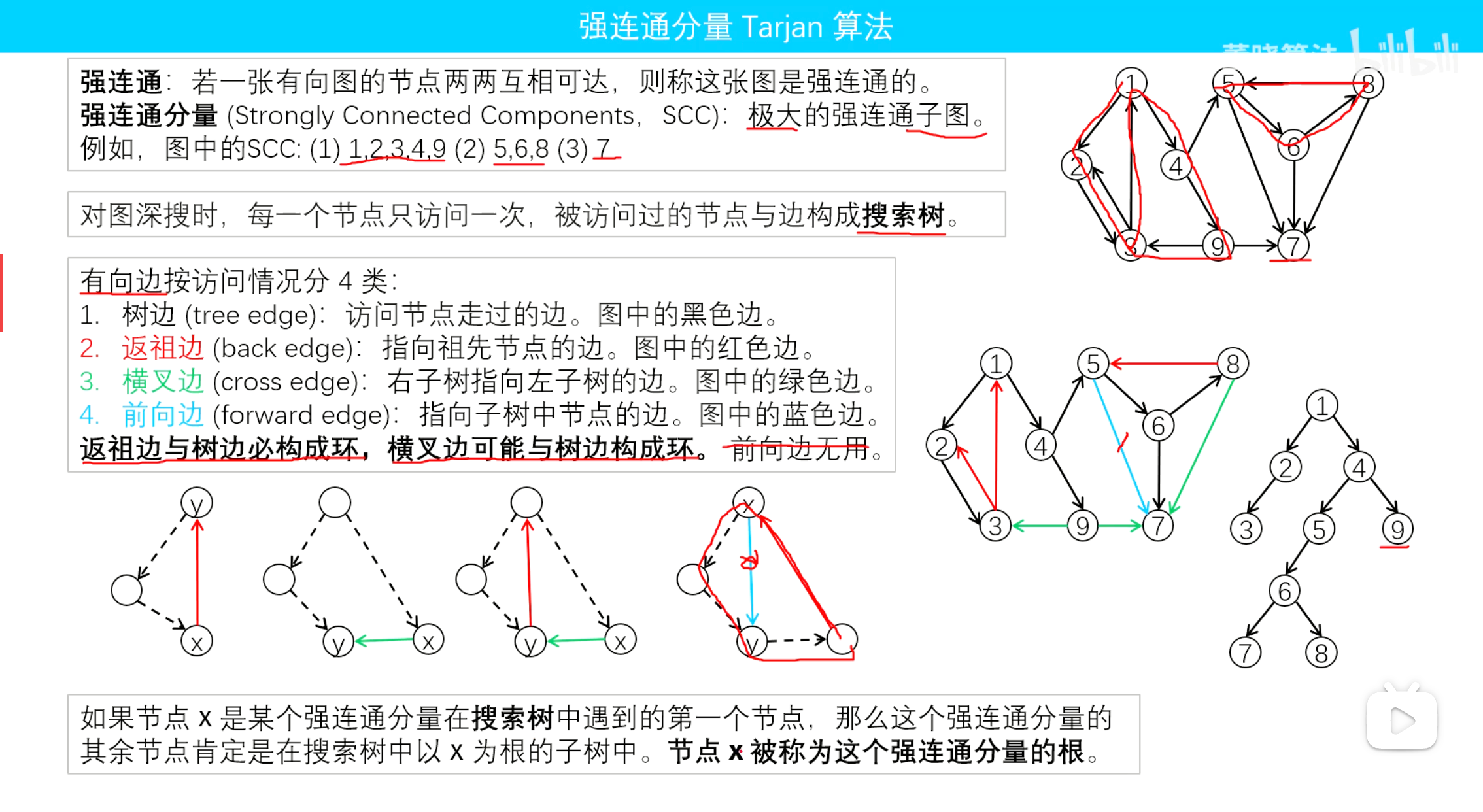
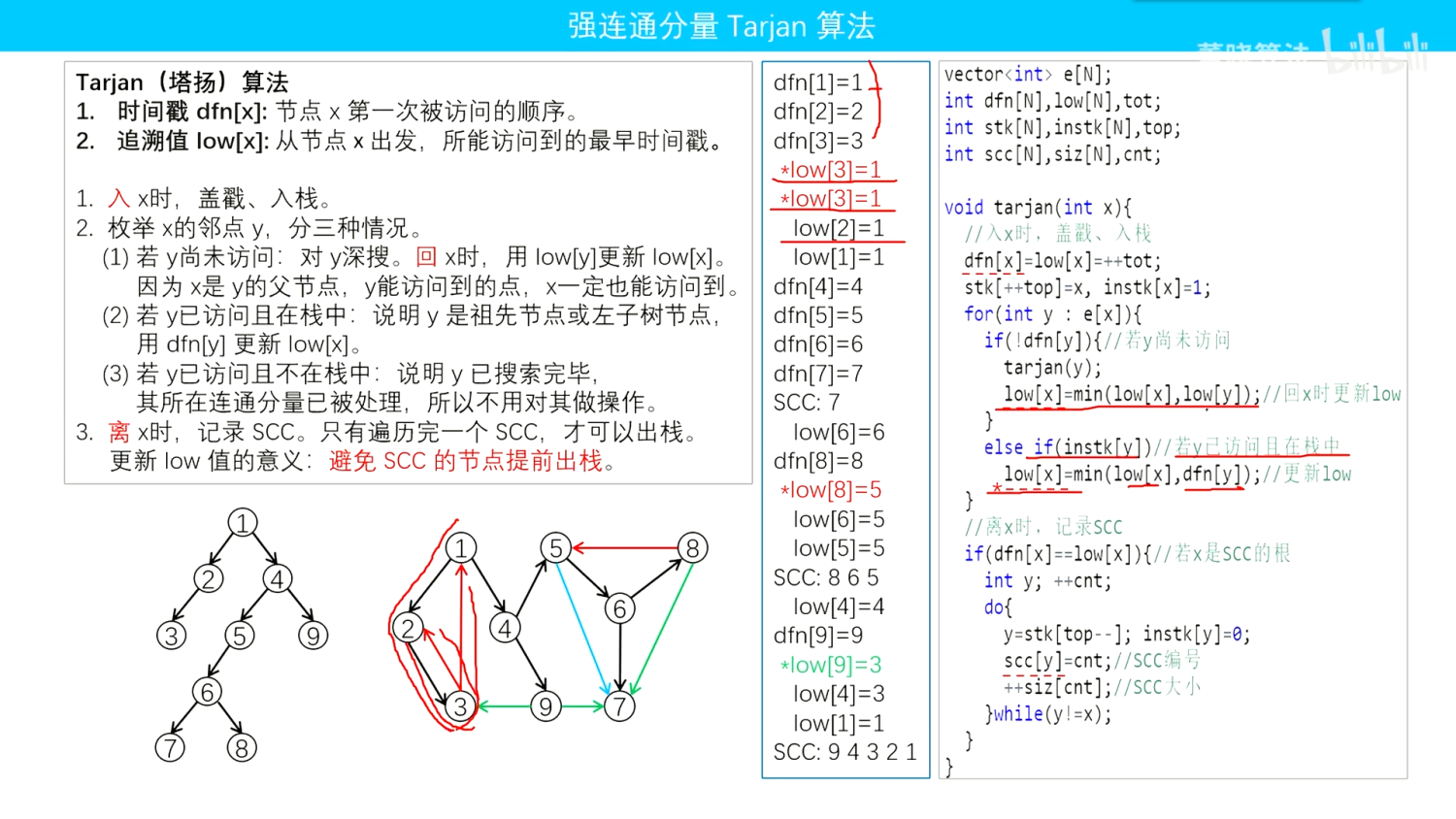
默写tarjan算法梳理的思路:
- 加时间戳;
- 放入栈中,做好标记;
- 遍历邻点:
- 如果没遍历过,tarjan一遍,用low[j]更新最小值low;
- 如果在栈中,用dfn[j]更新最小值low
- 找到最高点:
- scc个数++
- do-while循环:从栈中取出每个元素;标志为出栈;对元素做好属于哪个scc;该scc中点的数量+ +
vector<int> e[N];
int dfn[N],low[N],tot;
int stk[N],instk[N],top;
int scc[N],siz[N],cnt;
void tarjan(int x){
//入x时,盖戳、入栈
dfn[x]=low[x]=++tot;
stk[++top]=x,instk[x]=1;
for(int y : e[x]){
if(!dfn[y]){//若y尚未访问
tarjan(y);
low[x]=min(low[x],low[y]);//回x时更新low
}
else if(instk[y])//若y已访问且在栈中
low[x]=min(low[x],dfn[y]);//在x时更新low
}
//离x时,收集SCC
if(dfn[x]==low[x]){//若x是SCC的根
int y; ++cnt;
do{
y=stk[top--];
instk[y]=0;
scc[y]=cnt;//SCC编号
++siz[cnt];//SCC大小
}while(y!=x);
}
}
[USACO06JAN] The Cow Prom S
https://www.luogu.com.cn/problem/P2863
题目描述
有一个 n n n 个点, m m m 条边的有向图,请求出这个图点数大于 1 1 1 的强连通分量个数。
输入格式
第一行为两个整数 n n n 和 m m m。
第二行至 m + 1 m+1 m+1 行,每一行有两个整数 a a a 和 b b b,表示有一条从 a a a 到 b b b 的有向边。
输出格式
仅一行,表示点数大于 1 1 1 的强连通分量个数。
样例 #1
样例输入 #1
5 4
2 4
3 5
1 2
4 1
样例输出 #1
1
提示
数据规模与约定
对于全部的测试点,保证 2 ≤ n ≤ 1 0 4 2\le n \le 10^4 2≤n≤104, 2 ≤ m ≤ 5 × 1 0 4 2\le m\le 5\times 10^4 2≤m≤5×104, 1 ≤ a , b ≤ n 1 \leq a, b \leq n 1≤a,b≤n。
思路
tarjan求强联通分量,感觉使用vector记录强联通分量比较好,可以知道每个强联通分量里面有哪些点,也可以知道大小。
代码
/**
* https://www.luogu.com.cn/problem/P2863
*/
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e4 + 10;
vector<int> e[N];
int dfn[N], low[N], total, cnt;
stack<int> stk;
bool instk[N];
vector<int> scc[N];
void tarjan(int x) {
dfn[x] = low[x] = ++total;
stk.push(x), instk[x] = true;
for (auto y: e[x]) {
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (instk[y]) {
low[x] = min(low[x], dfn[y]);
}
}
if (dfn[x] == low[x]) {
int y;
cnt++;
do {
y = stk.top();
stk.pop();
instk[y] = false;
scc[cnt].push_back(y);
} while (y != x);
}
}
signed main() {
#ifndef ONLINE_JUDGE
freopen("test.in", "r", stdin);
freopen("test.out", "w", stdout);
#endif
int n, m;
cin >> n >> m;
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
e[x].push_back(y);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) {
tarjan(i);
}
}
int res = 0;
for (int i = 1; i <= cnt; i++) {
if (scc[i].size() > 1)
res++;
}
cout << res << endl;
return 0;
}
Checkposts
https://www.luogu.com.cn/problem/CF427C
题面翻译
题目描述
你的城市有N个路口。路口之间有一条单程道路。作为城市的市长,你必须确保所有路口的安全。
为了确保安全,你必须建造一些警察检查站。一个检查站只能建在一个路口。 如果有一个检查站在i路口,保护j的条件是:i==j或者警察巡逻车可以从i走到j,并且能回到i。
建造检查站要花一些钱。 由于城市的某些地区比其他地区更昂贵,在某些路口修建检查站可能比其他路口花费更多的钱。
你必须确定以确保所有路口的安全所需的最低资金。
此外,你必须找到以的最低价格和在最小数量的检查站确保安全的方案数。
如果其中任何一个路口包含其中一个检查点而不包含在另一个路口中,则两种方式是不同的。
答案模 1000000007(10^9+7)1000000007(10
9
+7)
输入输出格式
输入格式:
n (路口数)
n个数 (每个路口建检查站的花费)
m (以下m行是m条有向道路)
x y (一条从x到y的有向道路)
输出格式:
一行用空格分割的两个数:
最小花费 方案数
题目描述
Your city has $ n $ junctions. There are $ m $ one-way roads between the junctions. As a mayor of the city, you have to ensure the security of all the junctions.
To ensure the security, you have to build some police checkposts. Checkposts can only be built in a junction. A checkpost at junction $ i $ can protect junction $ j $ if either $ i=j $ or the police patrol car can go to $ j $ from $ i $ and then come back to $ i $ .
Building checkposts costs some money. As some areas of the city are more expensive than others, building checkpost at some junctions might cost more money than other junctions.
You have to determine the minimum possible money needed to ensure the security of all the junctions. Also you have to find the number of ways to ensure the security in minimum price and in addition in minimum number of checkposts. Two ways are different if any of the junctions contains a checkpost in one of them and do not contain in the other.
输入格式
In the first line, you will be given an integer $ n $ , number of junctions $ (1<=n<=10^{5}) $ . In the next line, $ n $ space-separated integers will be given. The $ i^{th} $ integer is the cost of building checkpost at the $ i^{th} $ junction (costs will be non-negative and will not exceed $ 10^{9} $ ).
The next line will contain an integer $ m (0<=m<=3·10^{5}) $ . And each of the next $ m $ lines contains two integers $ u_{i} $ and $ v_{i} (1<=u_{i},v_{i}<=n; u≠v) $ . A pair $ u_{i},v_{i} $ means, that there is a one-way road which goes from $ u_{i} $ to $ v_{i} $ . There will not be more than one road between two nodes in the same direction.
输出格式
Print two integers separated by spaces. The first one is the minimum possible money needed to ensure the security of all the junctions. And the second one is the number of ways you can ensure the security modulo $ 1000000007 $ $ (10^{9}+7) $ .
样例 #1
样例输入 #1
3
1 2 3
3
1 2
2 3
3 2
样例输出 #1
3 1
样例 #2
样例输入 #2
5
2 8 0 6 0
6
1 4
1 3
2 4
3 4
4 5
5 1
样例输出 #2
8 2
样例 #3
样例输入 #3
10
1 3 2 2 1 3 1 4 10 10
12
1 2
2 3
3 1
3 4
4 5
5 6
5 7
6 4
7 3
8 9
9 10
10 9
样例输出 #3
15 6
样例 #4
样例输入 #4
2
7 91
2
1 2
2 1
样例输出 #4
7 1
思路
利用tarjan算法求SCC进行缩点,然后对于每个点内,可以使用map来求这个点内的最小代价以及出现的次数,,每个点内必须要选一个最小代价即可,总方案数就是利用乘法原理,把每个点内最小代价出现的次数乘起来即可。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10, mod = 1e9 + 7;
vector<int> e[N], scc[N];
int dfn[N], low[N], st[N], cnt, total;//total是时间戳,cnt是SCC长度
stack<int> q;
int n, m;
int w[N];
void tarjan(int x) {
dfn[x] = low[x] = ++total;
q.push(x), st[x] = true;
for (auto y: e[x]) {
if (!dfn[y])tarjan(y), low[x] = min(low[x], low[y]);
else if (st[y]) low[x] = min(low[x], dfn[y]);
}
if (dfn[x] == low[x]) {
int y;
++cnt;
do {
y = q.top();
q.pop();
st[y] = false;
scc[cnt].push_back(y);
} while (y != x);
}
}
signed main() {
#ifndef ONLINE_JUDGE
freopen("../test.in", "r", stdin);
freopen("../test.out", "w", stdout);
#endif
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> w[i];
}
cin >> m;
for (int i = 1; i <= m; ++i) {
int x, y;
cin >> x >> y;
e[x].push_back(y);
}
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) tarjan(i);
}
vector<map<int, int>> cost(cnt + 1);
int mi = 0, res = 1;
for (int i = 1; i <= cnt; ++i) {
for (auto x: scc[i]) {
cost[i][w[x]]++;
}
for (auto [x, y]: cost[i]) {
mi += x;
res = (res * y) % mod;
break;
}
}
cout << mi << " " << res << endl;
return 0;
}