前言:以下是本人做学术研究时搜集整理的资料,供有相同研究需求的人员参考。
1. 合作博弈的一些概念
合作博弃中比较重要的问题是共赢状态下的利润分配问题,这关系到联盟的合作机制能否长期有效。这里首先介绍几个重要的概念:
(1)联盟
在n人博弈事件中,集合 ,
, 的任意子集
的任意子集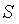 称为联盟(也包括空集),集合
称为联盟(也包括空集),集合 称为大联盟(grand coalition)。n个局中人的博弈最多能够形成
称为大联盟(grand coalition)。n个局中人的博弈最多能够形成 种联盟。
种联盟。
(2)特征函数(帕累托最优集)
在特定的一个n人博弈事件中, 为一个联盟,实值函数
为一个联盟,实值函数 可以解释为联盟当
可以解释为联盟当 合作时联盟
合作时联盟 的成员可以获得的最大收益或可节省的最多费用,通常认定博弈
的成员可以获得的最大收益或可节省的最多费用,通常认定博弈 具有特征函数
具有特征函数 。具有参与者集合
。具有参与者集合 的合作博弈的特征函数的集合记为
的合作博弈的特征函数的集合记为 。
。
一般地,特征函数满足超可加性:对于联盟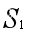 、
、 如果
如果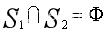 ,则
,则 ,即我们平时所说的协同效应。
,即我们平时所说的协同效应。
(3)联盟的分配方案
设博弈事件中的一个联盟中有m个参与者,即 ,其特征函数为
,其特征函数为 ,如果向量
,如果向量 ,满足
,满足 且
且 。则
。则 称是联盟的一个分配方案。
称是联盟的一个分配方案。
 为合作对策
为合作对策 中的分配的充分必要条件是以下等式成立:
中的分配的充分必要条件是以下等式成立:

,此时 。
。
其中 联盟
联盟 可以建立合作的条件下给参与者
可以建立合作的条件下给参与者 的支付。其中,
的支付。其中, 称为个体合理性条件,表示联盟
称为个体合理性条件,表示联盟 中的任何参与者,加入联盟后所获的效用要不少于加入联盟前的自己所获得的效用,否则它宁愿不加入这个联盟。而
中的任何参与者,加入联盟后所获的效用要不少于加入联盟前的自己所获得的效用,否则它宁愿不加入这个联盟。而 称为集体合理性条件,表示联盟中所有参与者所获得的效用应等于联盟的特征函数
称为集体合理性条件,表示联盟中所有参与者所获得的效用应等于联盟的特征函数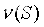 ,即联盟中的所有参与者分完联盟获得的所有效用。
,即联盟中的所有参与者分完联盟获得的所有效用。
把联盟的剩余看成是成本时,特征函数满足单调性的条件有:

(不是说联盟中成员越多,联盟节约的成本就越多)

(4)效用转移
效用转移是指参与者为了保证联盟整体的效用最大化,在实行联盟的最优决策方案时做出一定的牺牲,而所谓牺牲的效用值则转移到了其它参与者中。具有特征函数形式的合作博弈通常解释为可转移支付博弈(TU博弈)。
(5)协商机制
合作者通过有效的协商机制,建立一种公平的效用分配模式,使收益较少的协同运输的合作者可以从长期的合作中得到补偿,而收益较多的协同运输参与者在长期的合作中做出一定的让歩,最终达到一种平衡机制。协商机制影响着效用的分配机制,而效用的分配则影响到协同运输活动合作者参与联盟的积极性,关系到整个协同运输联盟的稳定。
这种合作机制是否可行的关键就在于每个合作者的利益是否都得到了保证,而每个合作者也是根据具体的环境,从自身的特征函数出发,分析自身的效益得失。对它们而言,这种合作是有选择的,它们参与合作的前提是使自身取得更多的效益, 这种合作是与自身的收益密不可分的。所以,判断一种合作机制得以维持的关键是正确处理好合作后的利益分配问题。而联盟正是由这样的理性决策者组成,它们关心的利益分配问题实际上也是联盟的最终效用分配问题。
2. 班轮联盟下合作博弈的概念
参考文献[1](2002年)给出班轮联盟下合作博弈的概念


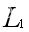 班轮公司经营的航线为A-B-A,
班轮公司经营的航线为A-B-A, 班轮公司经营的航线为B-C-B,不同航段间的运价以及成本由上表给出。当两家公司联盟后共同经营的航线为A-B-C-B-A,假设当公司单独经营航线时,航线A-B-A的年集装箱运输量为10万TEUs,航线B-C-B的年集装箱运输量为10万TEUs,当共同经营航线时,航段AC上产生的年集装箱运输量为5万TEUs(5万TEUs为从其他班轮公司经营的AC航段上吸引到的流量)。假定航线A-B-C-B-A上的收益按照1:1的比例进行分配,由表3可知,
班轮公司经营的航线为B-C-B,不同航段间的运价以及成本由上表给出。当两家公司联盟后共同经营的航线为A-B-C-B-A,假设当公司单独经营航线时,航线A-B-A的年集装箱运输量为10万TEUs,航线B-C-B的年集装箱运输量为10万TEUs,当共同经营航线时,航段AC上产生的年集装箱运输量为5万TEUs(5万TEUs为从其他班轮公司经营的AC航段上吸引到的流量)。假定航线A-B-C-B-A上的收益按照1:1的比例进行分配,由表3可知, 和
和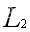 联合经营航线所获得的收益都要比各自单独经营航线所获收益高。当调整利益分配比例为1:3时,
联合经营航线所获得的收益都要比各自单独经营航线所获收益高。当调整利益分配比例为1:3时,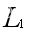 公司只能分得全部收益的四分之一,明显小于独立经营航线时所能获得的收益。对于公司
公司只能分得全部收益的四分之一,明显小于独立经营航线时所能获得的收益。对于公司 来说,如果合作所能带来的好处(也称“剩余”或“得益”)与不合作相比,相对较低时,联盟会不稳定。
来说,如果合作所能带来的好处(也称“剩余”或“得益”)与不合作相比,相对较低时,联盟会不稳定。
合作博弈是指每个参与者,为了实现整体效益的最大化,在自身效益不减少的前提下,同博弈活动其他的参与者建立合作伙伴关系,实施信息共享、协同决策,最终达到共赢的目的。稳定的合作需要联盟中的每个参与人都认为自己得到了公平的对待,即自己得到了联盟剩余中应得的那一部分,否则联盟就会破裂。合作(或者联盟的)博弈从宏观的角度研究博弈,关注可以用有约束力的承诺来得到可行的结果。与非合作博弈不同,合作博弈的分析单位是联盟,考虑的是参与人之间如何组建不同的联盟以实现协议的目标。
3. 班轮联盟下合作的具体形式
战略联盟:尽管理论界对企业战略联盟的认识存在一定差异,但在本质上基本达成以下几点共识:
(1)企业战略联盟可以看作是由两个或更多企业为了共同利益达成的有合作协议的联盟;
(2)企业战略联盟是一种超越一般交易关系的合作关系,仍保持各自的独立性和平等地位,不存在控制和被控制的隶属关系;
(3) 战略联盟企业间的合作不一定是全方位的,可能在某些领域合作而又在其他领域竞争。
合作的目的是找到顾客需求与联盟内成员的可利用运输资源之间的均衡,通过交换联盟内成员获得的顾客运输需求。
合作有横向合作和纵向合作两种形式。横向合作(horizontal cooperation)指合作的双方是同一阶层的,例如两个承运人之间的合作;纵向合作(vertical cooperation)指合作的双方是不同阶层的,例如制造商和承运人之间的合作。托运人合作的目标是在某一条运输路线上各自的运输需求能够捆绑在一起委托承运人进行运输。
三种集装箱船舶的运作策略[13]:
(1)舱位共享协定:承运人之间事先确定船舶容量共享的比例,既在一个计划期内确定舱位共享系数 (
(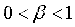 )。在实际运作中,当两家承运人在相同的航线上存在集装箱作业但是挂靠港口的离开时间不同时,舱位共享协定可以为时间敏感的货物提供更好的服务。舱位共享协定在实际运作中是承运人间的部分合作实例。
)。在实际运作中,当两家承运人在相同的航线上存在集装箱作业但是挂靠港口的离开时间不同时,舱位共享协定可以为时间敏感的货物提供更好的服务。舱位共享协定在实际运作中是承运人间的部分合作实例。
(2)完全共享策略:旨在实现承运人间的完全合作,通过完全共享需求信息和船舶资源共享。这一策略的现实要求合作承运人联合优化船舶离港时间和船舶的装货计划。在实际运作中,完全共享策略也要求合作承运人间共享收益、货运信息以及操作成本。这一策略在航运业还未被完全实践,因此在学术上很有理论研究的必要。
(3)非合作策略:旨在构建船舶调度和安排货运流量分配最小化单个承运人的运作成本,但是不包含与其他外部承运人间的资源共享。这是传统的船舶运作策略,可以将该策略作为基准与船舶调度的合作策略进行比较,从而判定船舶调度合作策略的有效性。
存在N家班轮公司组成的大联盟G,S为G的子集,表示G中任意公司的联盟。公司之间联盟的前提是航线服务网络不完全重合,即纵向联盟,例如,班轮公司 经营的航线上船舶只能挂靠M、N两个港口,班轮公司
经营的航线上船舶只能挂靠M、N两个港口,班轮公司 经营的航线上船舶只能挂靠N、T两个港口,这时两家班轮公司存在联盟的可能性,联盟后班轮公司在共同经营的航段实行统一定价。(不关心什么样的公司能够加入联盟,关心的是在联盟形成后合作的方式以及得益的分配)
经营的航线上船舶只能挂靠N、T两个港口,这时两家班轮公司存在联盟的可能性,联盟后班轮公司在共同经营的航段实行统一定价。(不关心什么样的公司能够加入联盟,关心的是在联盟形成后合作的方式以及得益的分配)
判断联盟是否稳定的条件有两个:
(1) ;(满足超可加性)(集体合理性)
;(满足超可加性)(集体合理性)
(2) 。(个体合理性)
。(个体合理性)
上述条件(1)表示班轮公司加入联盟后,联盟的总效用值不低于班轮公司合作前的各自效用值的加和,否则组建这个联盟就没有意义;条件(2)表示班轮公司加入联盟后所得到的效用值不低于自身独立完成运输活动(即加入联盟前)的效用值。
3.1 将船舶当做是市场投入
考虑n个企业形成的联盟,每个企业的全部资源记为1, 为第i个企业所拥有的将对联盟核心竞争力做出贡献的企业资源,
为第i个企业所拥有的将对联盟核心竞争力做出贡献的企业资源, 。为简单起见,记构成联盟核心竞争力的所有资源总和为
。为简单起见,记构成联盟核心竞争力的所有资源总和为 。
。
多个企业组建联盟的核心竞争力不是所有成员企业贡献资源的简单和,而应当体现出协同效应,因此,我们定义联盟的特征函数为联盟拥有的资源的函数: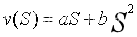 。
。
如果b=0,表明企业组成联盟后的合作收益是不变的,即企业联盟的收益等于联盟成员企业组成联盟之前收益的简单和;如果b>0,表明联盟出现协同效应,联盟的总收益大于不联盟时各单个企业的收益之和。以两企业为例,它们对联盟贡献的资源分别为 和
和 ,不联盟时各自的收益分别为
,不联盟时各自的收益分别为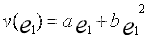 、
、 ,联盟后的收益为
,联盟后的收益为 ,显然,
,显然,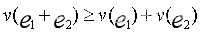 ,表明联盟后的收益大于不联盟时各企业单干的收益之和,联盟产生协同效应,当且仅当
,表明联盟后的收益大于不联盟时各企业单干的收益之和,联盟产生协同效应,当且仅当 时,
时,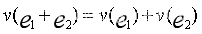 成立。
成立。
设有三家企业组建联盟,各家企业贡献给联盟的资源分别为 =0.4,
=0.4,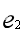 =0.3,
=0.3, =.05,为计算方便,我们取a=b=1,计算联盟博弈特征函数如表5-1(即联盟博弈收益表)。
=.05,为计算方便,我们取a=b=1,计算联盟博弈特征函数如表5-1(即联盟博弈收益表)。

应用公式 得三家企业的Shapley值为
得三家企业的Shapley值为
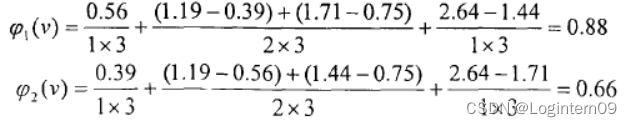
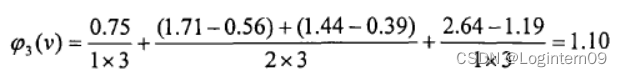
由于三家企业联盟产生协同效用,共同的效用为2.64,三家企业各得效用0.88,0.66,1.10。如果将效用值2.64转化为具体的效益值,三家企业可以按照各自所得效用的比例获得相应的收益。
设某航线上有n家班轮公司提供相同或者相近的服务,大家共同拥有一个可以提供利润的市场,但市场上的货运需求不是无限大的。由于货运需求是有限的,只有让某些班轮公司的船舶运力得到充分的利用,但投放到该航线上的运力超过这个限度时,则所有船舶载箱率都不理想,班轮公司的利润不理想甚至亏损。假设各班轮公司清楚的知道该航线上的货运需求量是多少,也知道自己在不同运力水平下的利润情况,并且n家班轮公司同时决定在该航线上投放多少运力,则可以将此问题成是一个完全静态博弈。
参考文献
[1]Dong Wook Song, Photis m.Panayides. A conceptual application of cooperative game theory to liner shipping strategic alliances[J]. maritime Policy & management,2002,29(3):285-301.
[13]Lei Lei,Chunxing Fan,Maria Boile,Sotiris Theofanis. Collaboration vs. non-collaborative container-vessel scheduling[J]. Transportation Research Part E,2008,44(3):504-520.
![[附源码]Python计算机毕业设计SSM基于框架的毕业生就业管理系统(程序+LW)](https://img-blog.csdnimg.cn/82c2cc0290f24ab4aa12e4ec864aaef0.png)

![[附源码]计算机毕业设计基于web的建设科技项目申报管理系统Springboot程序](https://img-blog.csdnimg.cn/dc00dcc661e14098bbf71efa71c0f3cf.png)
![[附源码]计算机毕业设计家庭教育appSpringboot程序](https://img-blog.csdnimg.cn/7af6d1215fab41539acff129576f759f.png)