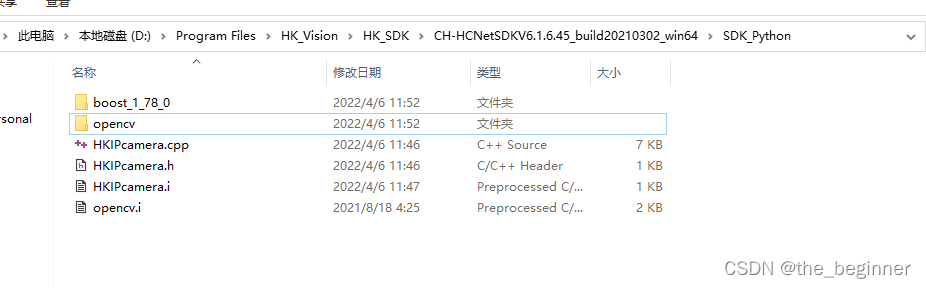
人工神经网络分为两个阶段:
1 :接收来自其他n个神经元传递过来的信号,这些输入信号通过与相应的权重进行
加权求和传递给下个阶段。(预激活阶段)
2:把预激活的加权结果传递给激活函数
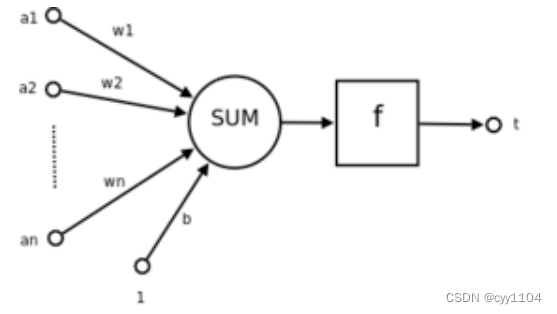
sum :加权
f:激活函数
神经元
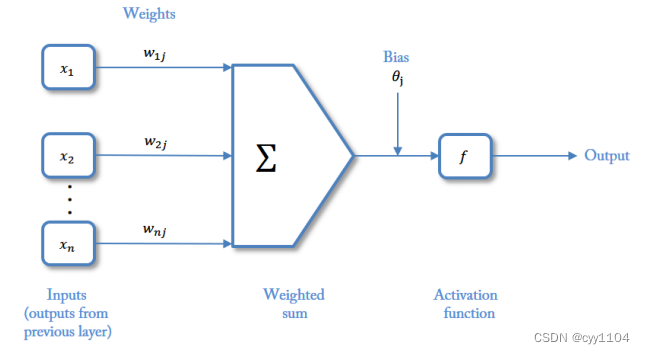
神经元是组成神经网络的最基本单位,它起初来源于人体,模仿人体的神经元,功能也与人体的神经元一致,得到信号的输入,经过数据处理,然后给出一个结果作为输出或者作为下一个神经元的输入
•
输入:是特征向量。特征向量代表的是变化的方向。或者说,是最能代表这个事物的特征的方
向。
•
权重(权值):就是特征值。有正有负,加强或抑制,同特征值一样。权重的绝对值大小,代
表了输入信号对神经元的影响的大小。
-----------------------------------------------------------------------------------------------------------------------------
最简单的把这两组特征向量分开的方法?

ax_+by+c=0 ->y = kx+b ->y=wx+b
把上式推广到n维空间:
h = a1x1+a2x2+...+anxn+a0 = 0
神经元就是当h大于0时输出1,h小于0时输出0这么一个模型,它的实质就是把特征空间一切两半,认为两
半分别属于两个类。
-----------------------------------------------------------------------------------------------------------------------------
神经元的缺点:只能一刀切

解决方法->多层神经网络
-----------------------------------------------------------------------------------------------------------------------------
神经网络
• 神经网络是一种运算模型,由大量的节点(神经元)和之间相互的联接构成。
• 每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。
• 网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
• 单层神经网络(感知器)
-----------------------------------------------------------------------------------------------------------------------------
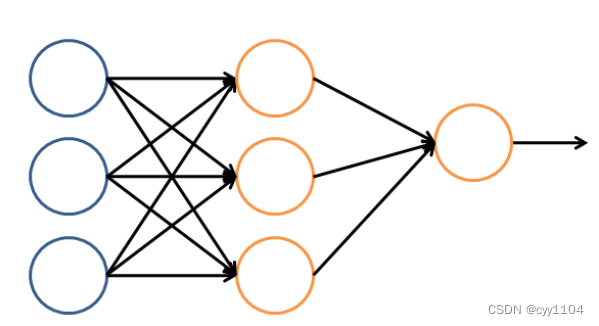
多层神经网络
•
神经网络是由多个神经元组合而成,前一个神经元的结果作为后一个神经元的输入,依次组合而成,神经网络一般分为三层,第一层作为输入层,最后一层作为输出层,中间的全部是隐含层。
•
理论证明,任何多层网络可以用三层网络近似地表示。
•
一般凭经验来确定隐藏层到底应该有多少个节点,在测试的过程中也可以不断调整节点数以取得最佳效果。
-----------------------------------------------------------------------------------------------------------------------------
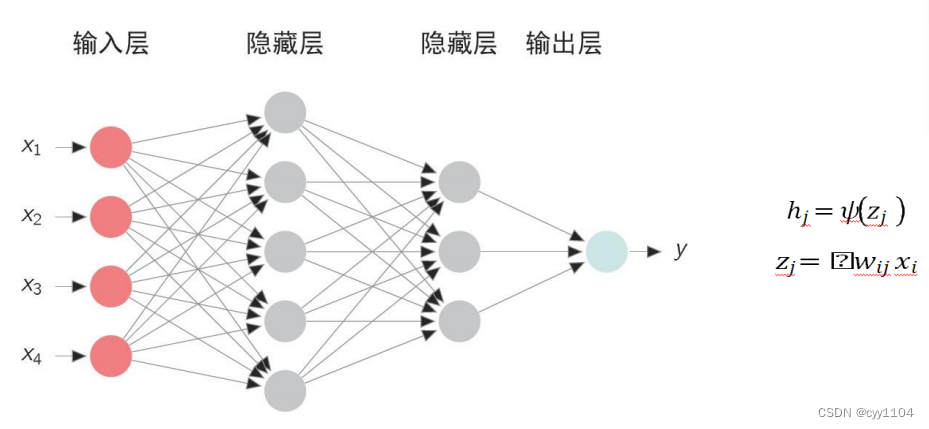
前馈神经网络
•
人工神经网络模型主要考虑网络链接的拓扑结构、神经元特征、学习规则等。
•
其中,前馈神经网络也称为
多层感知机
-----------------------------------------------------------------------------------------------------------------------------
激活函数
•
激活函数是神经网络设计的一个核心单元。
•
在神经网络中,把处于在活跃状态的神经元称为激活态,处于非活跃状态的神经元称为抑制态。激活函数赋予了神经元自我学习和适应的能力。
•
激活函数的作用是为了在神经网络中引入非线性的学习和处理能力。
•
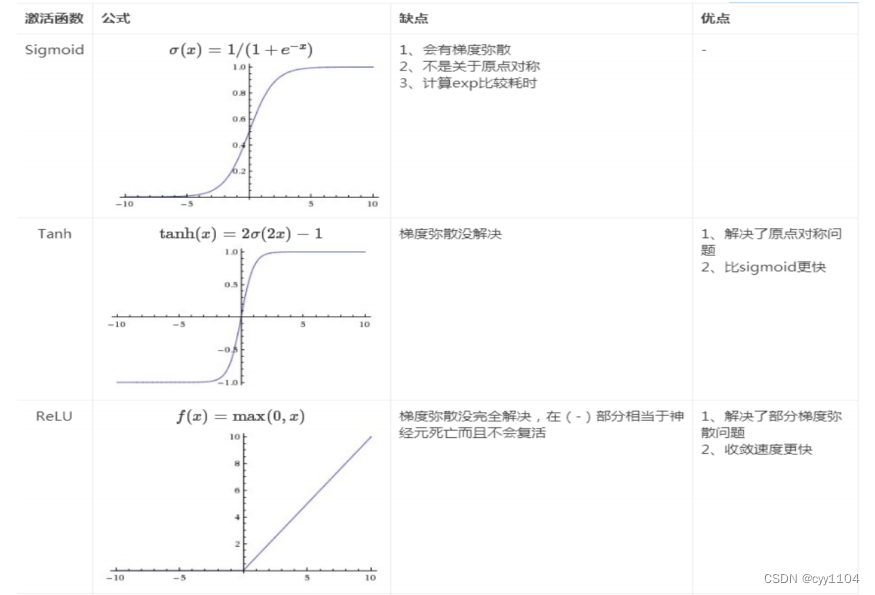
常用的激活函数(满足 1 非线性 2 可微性 3 单调性)
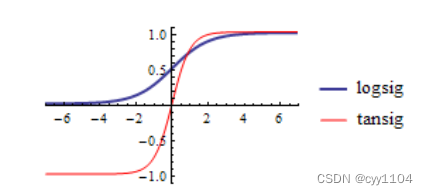
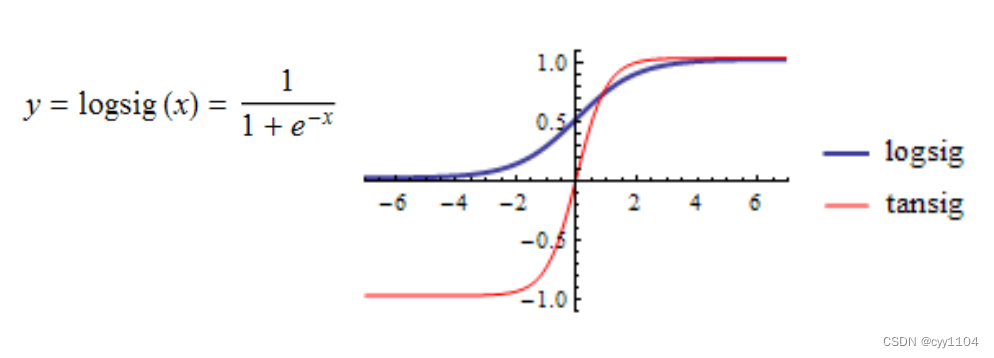
1 sigmoid函数


2 tanh函数 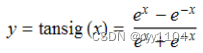
3 ReLU函数 f(x) = max (0, x)
-----------------------------------------------------------------------------------------------------------------------------
sigmoid主要有两个缺点:
1. 梯度饱和,看图可知,两边数值的梯度都为0;
2. 结果的平均值不为0,这是我们不希望的,因为这会导致后层的神经元的输入是非
0均值的信号,这会对梯度产生影响
-----------------------------------------------------------------------------------------------------------------------------
激活函数
-tanh
 配图错了,见后图
配图错了,见后图
-----------------------------------------------------------------------------------------------------------------------------
激活函数
-
线性整流层
RELU
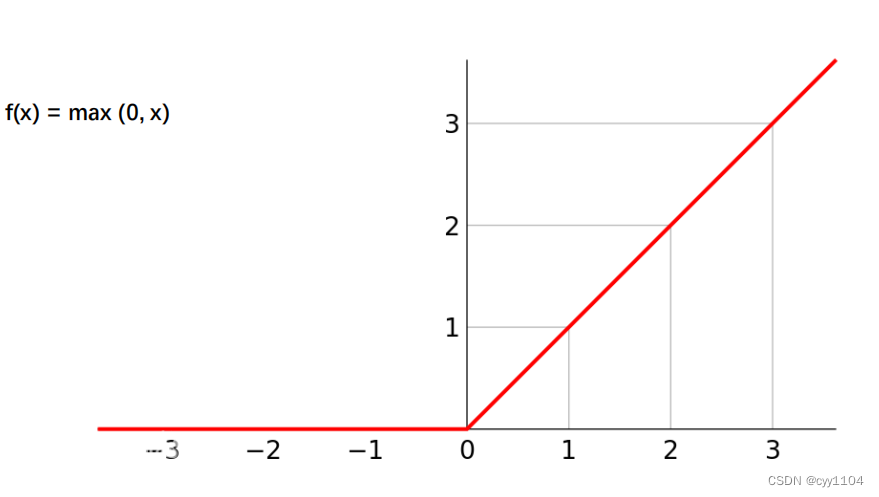

ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变,这种操作
被称为
单侧抑制
。
正因为有了这单侧抑制,才使得神经网络中的神经元也具有了稀疏激活性。
当
模型增加N层之后,理论上ReLU神经元的激活率将降低2的N次方倍
。
-----------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
•
任何算法得以运行,都必须依靠特定的数据结构,而用于将各种数据统一封装并输入网络模型的数据结构叫tensor,也就是张量。张量在不同的情况下存有不同的形式。
•
张量一大特征是维度,一个0维张量就是一个常量。在Python中,一个张量的维度可以通过读取它的ndim属性来获取。(我们常用的数组就等价与一维张量,一个二维数组就是一个二维张量)
•
所谓n维张量,其实就是一维数组,数组中的每个元素都是n-1维张量。由此可见,3维张量其实就是一个一维数组,数组中的每个元素就是2维数组。

-----------------------------------------------------------------------------------------------------------------------------
设计神经网络
1、使用神经网络训练数据之前,必须确定神经网络的层数,以及每层单元的个数
2、特征向量在被传入输入层时通常要先标准化到0-1之间(为了加速学习过程)
3、离散型变量可以被编码成每一个输入单元对应一个特征值可能赋的值
比如:特征值A可能取三个值(a0, a1, a2), 可以使用3个输入单元来代表A。
如果A=a0, 那么代表a0的单元值就取1, 其他取0;1,0,0
如果A=a1, 那么代表a1的单元值就取1,其他取0,以此类推 0,1,0
4、神经网络既可以用来做分类(classification)问题,也可以解决回归(regression)问题
(1)对于分类问题,如果是2类,可以用一个输出单元表示(0和1分别代表2类);如果多于2类,则每
一个类别用一个输出单元表示 1 0 0 01 0
(2)没有明确的规则来设计最好有多少个隐藏层,可以根据实验测试和误差以及精准度来实验并改进。
-----------------------------------------------------------------------------------------------------------------------------
深度神经网络
&
深度学习
•
传统的神经网络发展到了多隐藏层的情况,
•
具有多个隐藏层的神经网络被称为深度神经网络,基于深度神经网络的机器学习研究称
之为深度学习。
•
如果需要细化和区分区别,那么,深度神经网络可以理解为对传统多层网络进行了结构、
方法等方面的优化。

-----------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------