目录
- 一. 🦁 前言
- 二. 🦁 各种树的知识点
- 1. 树
- 1.1 概念
- 1.2 属性
- 1.3 常考性质
- 1.4 树转换成二叉树
- 1.5 森林转换为二叉树
- 1.6 二叉树转换为森林
- 1.7 树的遍历
- 1.8 森林的遍历
- 2. 二叉树
- 2.1满二叉树
- 2.2 完全二叉树
- 2.3二叉排序树
- 2.4 平衡二叉树
- 2.5 二叉树常考性质
- 2.6 二叉树存储结构
- 1. 顺序存储
- 2. 链式存储
- 2.7二叉树的遍历
- 1. 先序遍历
- 2. 中序遍历
- 3. 后序遍历
- 4. 层序遍历
- 3. 线索二叉树
- 4. 哈夫曼树与哈夫曼编码
- 4.1 哈夫曼树的构造
- 5. 并查集
- 5.1 初始版本
- 5.2 优化版本
- 三. 🦁 总结
一. 🦁 前言
根据王道考研数据结构总结出的知识点,以下是文章整体大纲:
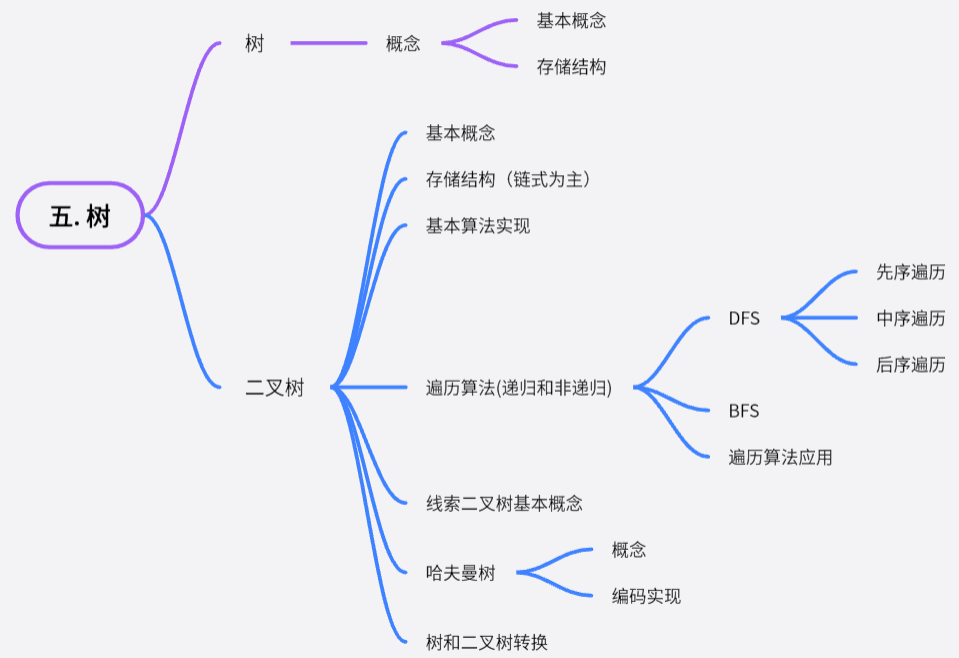
二. 🦁 各种树的知识点
1. 树
1.1 概念
树是n个结点的有限集合,n = 0时称为空树,这是一种特殊情况。任意一棵非空树中应满足:
- 有且仅有一个特定的称为根的节点
- 当n>1时,其余结点可分为m个互不相交的有限集合T1、T2、T3……Tm;每个集合又称为根结点的子树。
1.2 属性
-
结点的深度:从上往下数;
-
结点的高度:从下往上数;
-
树的高度:总共多少层
-
结点的度:有几个孩子
-
树的度:树中结点的度的最大值
1.3 常考性质
- 结点数 = 总度数+1
- 度为m的树和m叉树
度为m的树是一定存在一个结点,它的度为m,且树非空;m叉树是指任意结点的度≤m,可以为空;
- 度为m的树第i层至多有m的i-1次方个结点(i>=1)

- 高度为h的m叉树至少有h个结点;高度为h,度为m的树至少有h+m-1个结点。

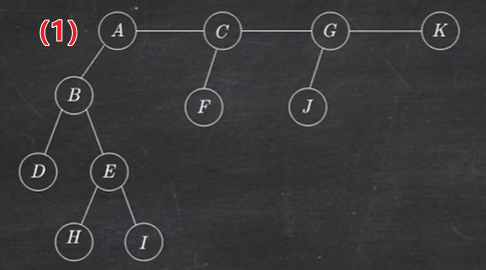
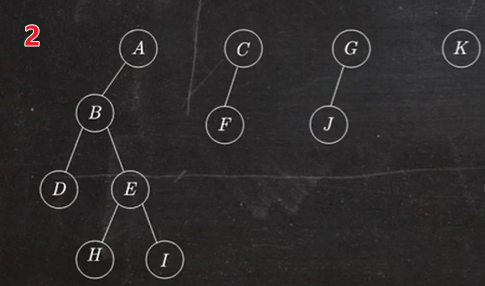
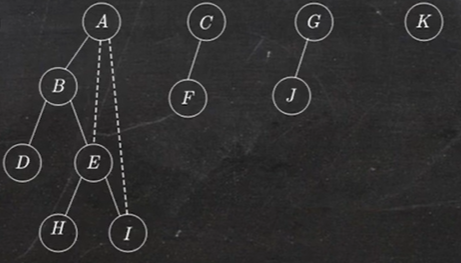
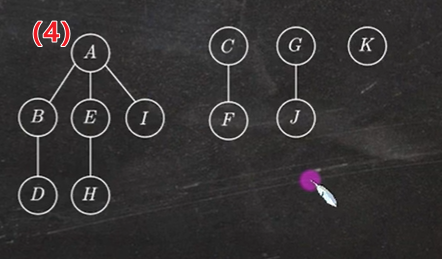
1.4 树转换成二叉树
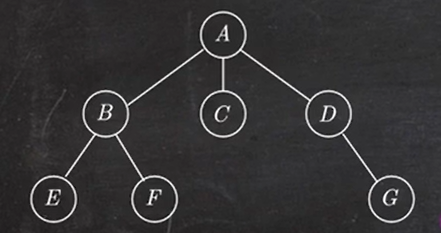
树转换成二叉树的画法:
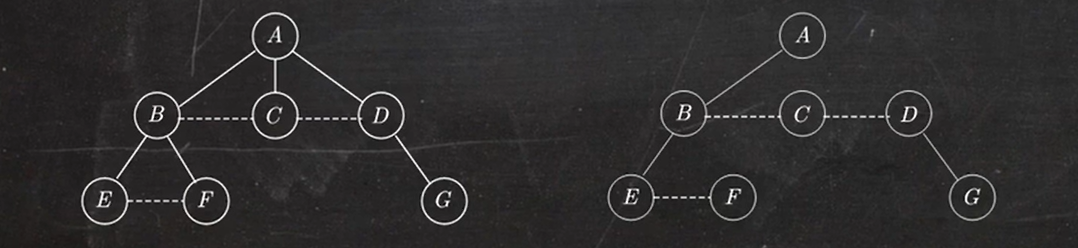
- 在兄弟结点之间加一条线;
- 对每个结点,只保留它与第一个孩子的连线,抹去与其他孩子的连线;
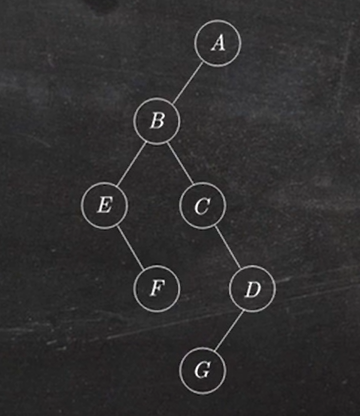
- 以树根为轴心,顺时针旋转 45°
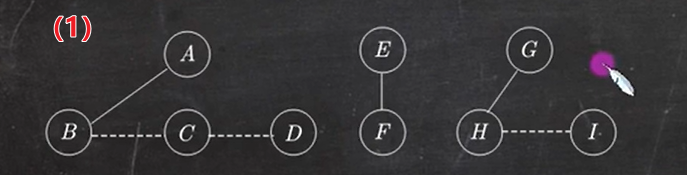
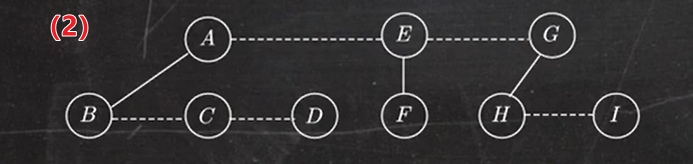
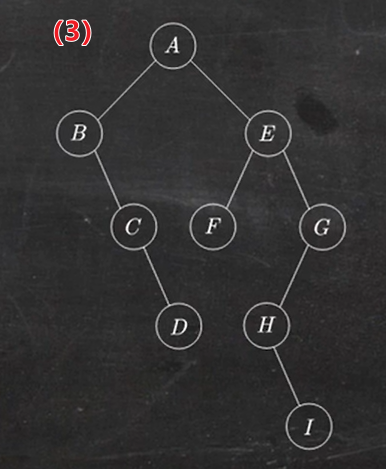
1.5 森林转换为二叉树
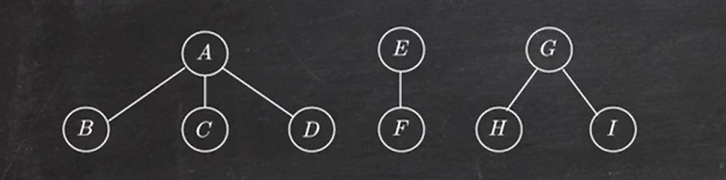
森林转换成二叉树的画法:
- 将森林中的每棵树转换成相应的二叉树
- 每棵树的根也可视为兄弟结点,在每棵树之间加一根连线
- 以第一棵树的根为轴心顺时针旋转 45°
1.6 二叉树转换为森林
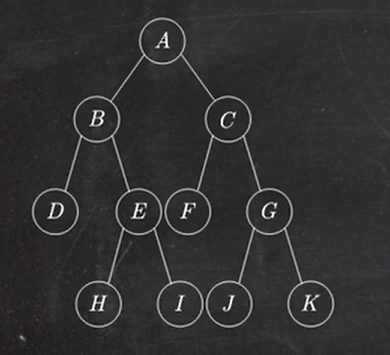
就是将森林转换为二叉树的逆做法
1.7 树的遍历
树的遍历: 用某种方式访问树中的每个结点,且仅访问一次
先序遍历:先根后子树
后根遍历:先子树后根
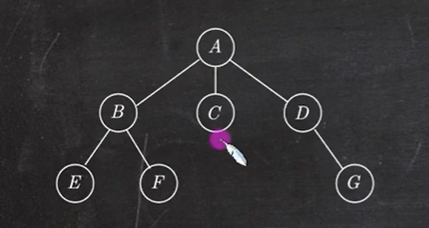
先根遍历序列为:ABEFCDG 对应二叉树中的先序遍历
后根遍历序列为:EFBCGDA 对应二叉树中的中序遍历
1.8 森林的遍历
先序遍历:先根后子树
中序遍历:先子树后根
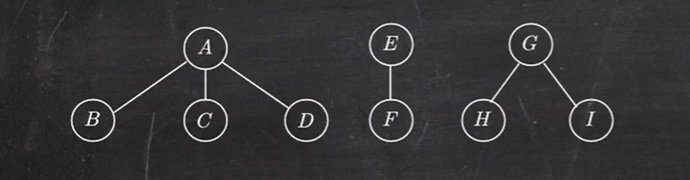
先序遍历序列为:ABCDEFGHI 对应二叉树的先序遍历
中序遍历序列为:BCDAFEHIG 对应二叉树的中序遍历
2. 二叉树
二叉树是n个结点的有限集合;
2.1满二叉树
一棵高度为h,且含有2的h次方-1个结点的二叉树;
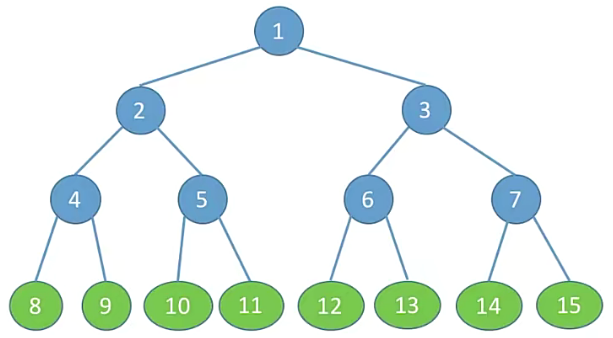
特点:
- 只有最后一层有叶子结点;
- 不存在度为1的结点;
- 按层序从1开始编号,结点为i的左孩子结点为2i;右孩子为2i+1;结点i的父结点为i/2;
2.2 完全二叉树
当且仅当每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树;
特点:
- 只有最后两层可能有叶子结点;
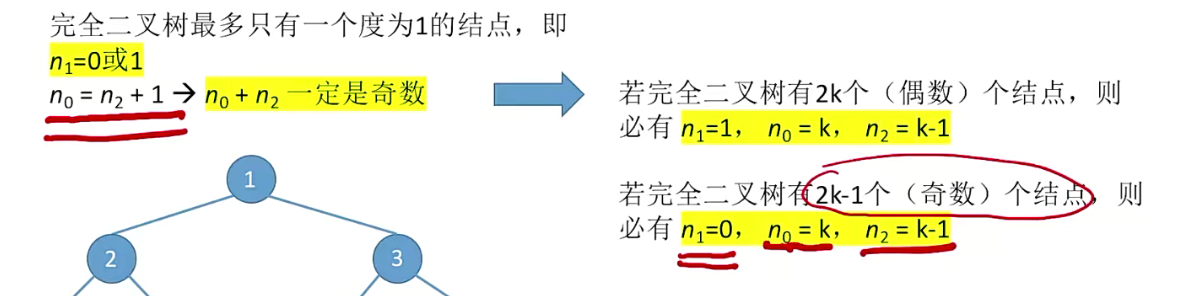
- 最多只有一个度为1的结点;
- i ≤ n/2为分支结点,i > n/2为叶子结点;
- 如果一个完全二叉树某结点只有一个孩子,则这个一定是左孩子;
2.3二叉排序树
- 左子树的所有结点均小于根结点;
- 右子树的所有结点均大于根结点;
- 左子树和右子树又各是一棵二叉排序树
2.4 平衡二叉树
树上任一结点的左子树和右子树的深度之差不超过1;
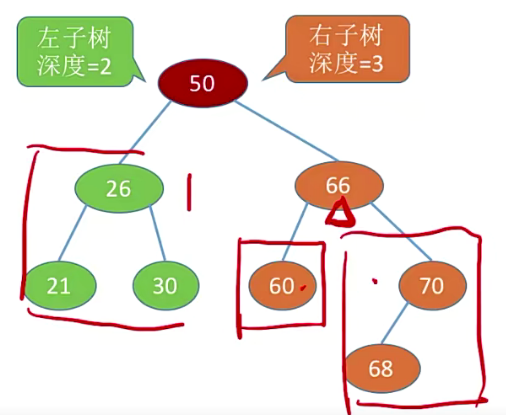
2.5 二叉树常考性质
- 设非空二叉树中度为0、度为1、度为2的结点个数分别为n0、n1、n2,则n0 = n2 +1(叶子结点永远比二分支结点多一个);

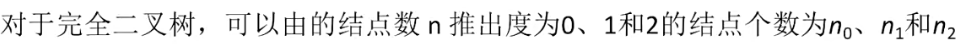

2.6 二叉树存储结构
1. 顺序存储
使用数组实现顺序存储。一定要把二叉树的结点编号与完全二叉树对应起来。
- i 的左孩子 — 2i+1
- i 的右孩子 — 2i+2
- i 的父节点 — 『(i-1)/2』
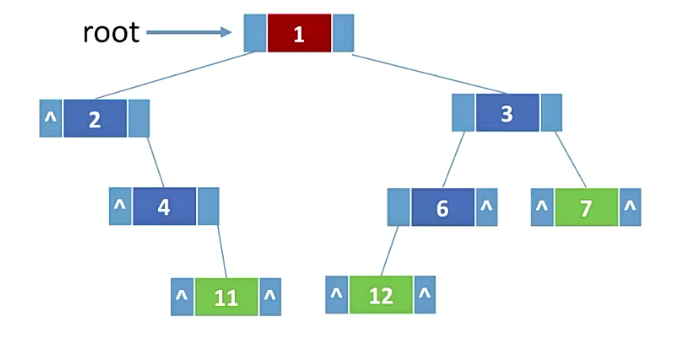
2. 链式存储
struct ElemType{
int value;
}
typedef struct BiTNode{
ElemType data; //数据域
struct BiTNode *lchild; //左孩子指针
struct BiTNode *rchild; //右孩子指针
}BiTNode,*BiTree;
假设二叉树有n个结点,那么一定会有2n个指针,共有n+1个空链域;
二叉树操作:
// 定义一棵空树
BiTree root = null;
// 插入根节点
root = (BiTree) malloc(sizeof(BiTNode));
root->data = {1};
root->lchild = NULL;
root->rchild = NULL;
//插入新结点
BiTNode * p = (BiTNode *)malloc(sizeof(BiTNode));
p->data = {2};
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p; //作为根节点的左孩子
2.7二叉树的遍历
1. 先序遍历
先序遍历(preOrder)的操作过程如下:
-
若二叉树为空,则什么也不做
-
若二义树非空:
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
void preOrder(BiTree root){ if(root != null){ visit(root); //访问根节点操作 preOrder(root->lchild); preOrder(root->rchild); } }void preOrder(BiTree root){ if(root != null){ visit(root); //访问根节点操作 preOrder(root->lchild); preOrder(root->rchild); } }
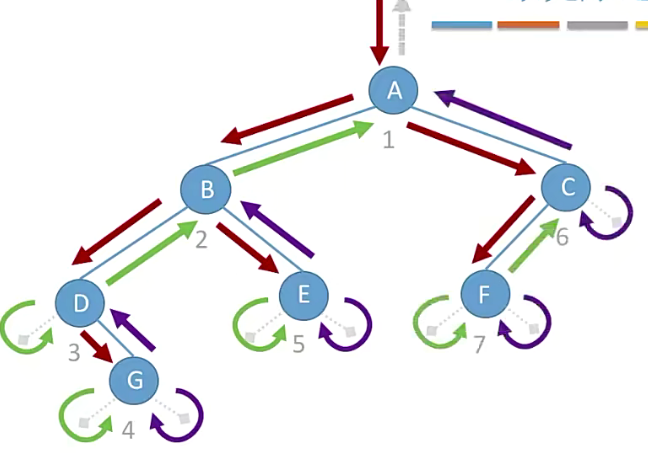
如下: 每个结点都会被访问三次。
2. 中序遍历
中序遍历(inOrder)的操作过程如下:
- 若二叉树为空,则什么也不做
- 若二义树非空:
- 中序遍历左子树
- 访问根结点
- 中序遍历右子树
void inOrder(BiTree root){
if(root != null){
inOrder(root->lchild);
visit(root); //访问根节点操作
inOrder(root->rchild);
}
}
3. 后序遍历
后序遍历(postOrder)的操作过程如下:
- 若二叉树为空,则什么也不做
- 若二义树非空:
- 后序遍历左子树
- 后序遍历右子树
- 访问根节点
void postOrder(BiTree root){
if(root != null){
postOrder(root->lchild);
postOrder(root->rchild);
visit(root); //访问根节点操作
}
}
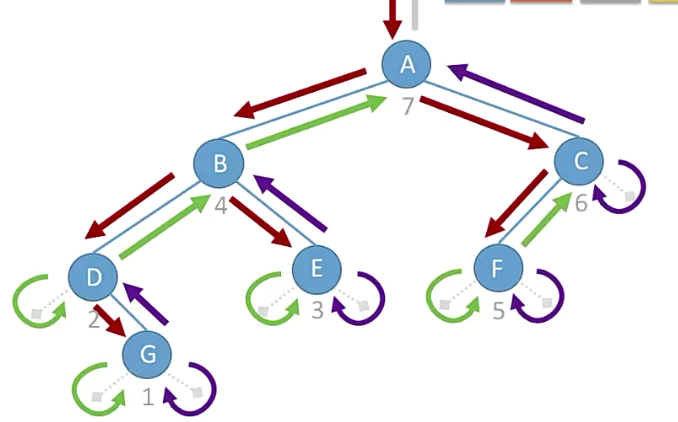
应用:求树的深度

4. 层序遍历
算法思想:
- 初始化一个辅助队列
- 根结点入队
- 若队列非空,则队头结点p出队,访问p,并将其左右孩子插入队尾(如果有的话)
- 重复步骤3,直到队列为空。
// 层序遍历
void levelOrder(BiTree root){
LinkQueue queue;
InitQueue(queue); //初始化队列
BiTree p;
enQueue(root); //根节点入队
while(!isEmpty(queue)){ //队列不为空则循环
deQueue(queue,p); //队头结点出队
visit(p);
if(p->lchild != NULL) enQueue(queue,p->lchild);
if(p->rchild != NULL) enQueue(queue,p->rchild);
}
}
队列定义如下:

3. 线索二叉树
4. 哈夫曼树与哈夫曼编码
权: 树中结点常被赋予一个代表某种意义的数值;
结点带权路径长度: 从树的根到任意结点的路径长度与该结点上权值的乘积;

哈夫曼树: 带权路径长度最小的二叉树
4.1 哈夫曼树的构造
构造哈夫曼树的步骤:
- 将所有结点分别作为仅含一个结点的二叉树;
- 构造一个新结点,从中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和;(意思即 每次找出两个权值最小的组成一棵二叉树)
- 从中删除刚才选出的两棵树,同时将新得到的树加入森林中;
- 重复步骤(2) 和 (3),直至剩下一棵树为止

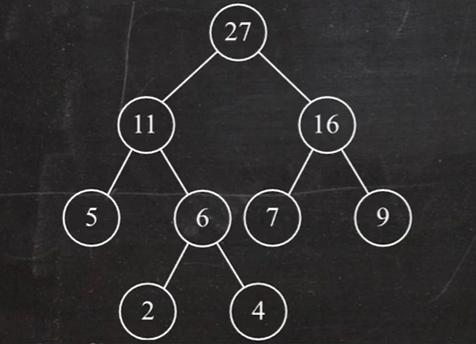
- 求哈夫曼编码就是在哈夫曼树的基础上将左子树的路径变成0,右子树的路径变成1,如下:
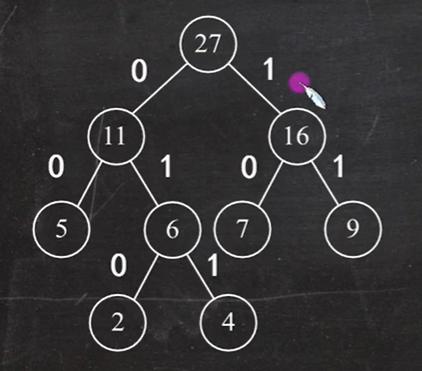
a的哈夫曼编码为:011
b的哈夫曼编码为:10
c的哈夫曼编码为:00
d的哈夫曼编码为:010
e的哈夫曼编码为:11
- ecabcbbe
- WPL = 5×2 + 2×3 + 4×3 + 7×2 + 9×2
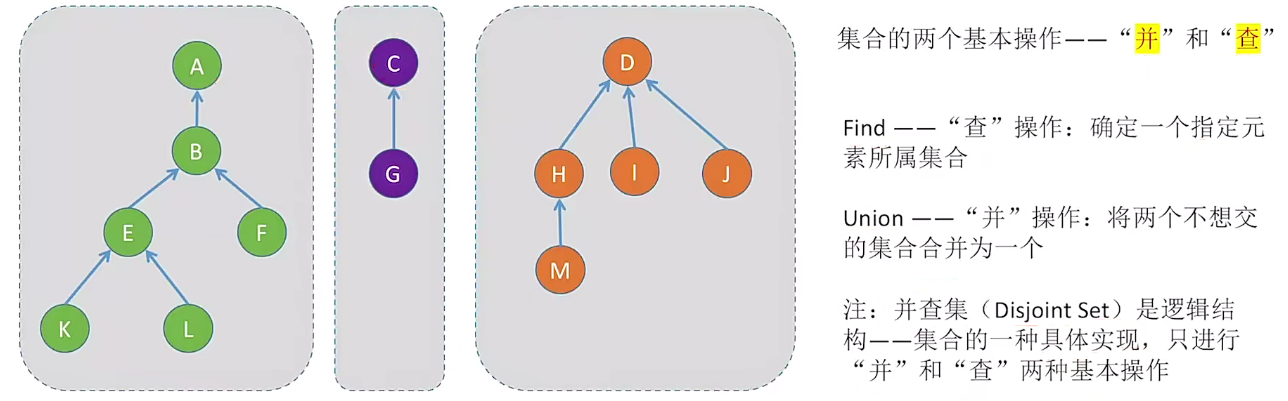
5. 并查集
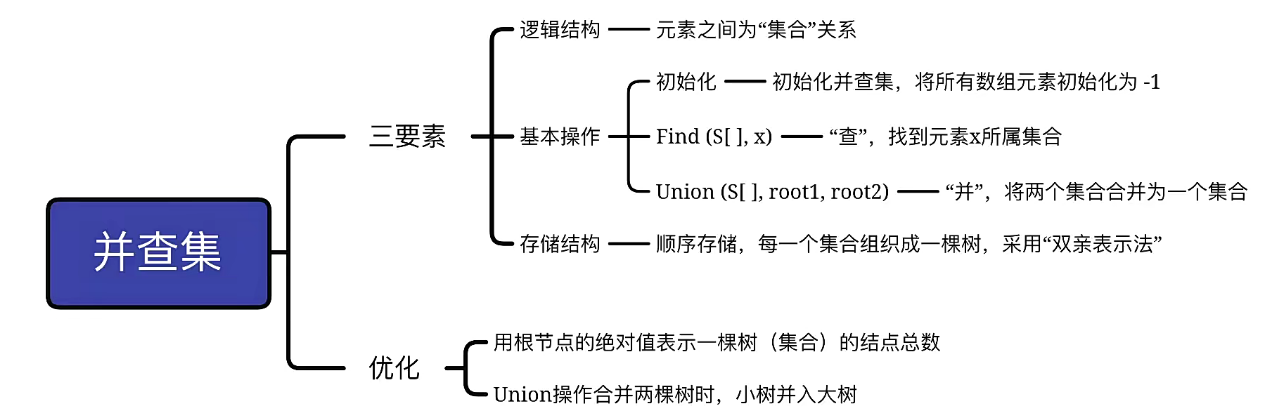
5.1 初始版本
public class unionFind{
// 初始化并查集
public void init(int[] nums){
Arrays.fill(nums,-1);
}
// 查操作:找x所属集合,返回x所属根节点
int find(int[] nums,int x){
while(s[x] >= 0){
x = s[x];
}
return x;
}
// 并操作:将两个集合合并为一体
public void union(int[] nums,int rootX,int rootY){
if(rootX == rootY) return;
nums[rootY] = rootX;
}
}
5.2 优化版本
public class unionFind{
// 初始化并查集
public void init(int[] nums){
Arrays.fill(nums,-1);
}
/**
* 并操作:使用根节点记录树的节点数目,让小树合并到大树上
* 该方法构造的树高不超过log2n]+1
* @param s
* @param x
* @param y
*/
public void union(int[] nums,int x,int y){
int root1 = find(nums,x);
int root2 = find(nums,y);
if (root1 == root2) return;
if(s[root2]>s[root1]){ //root2节点更少(负数)
s[root1] += s[root2]; //将小树的根节点数目加到大树根节点上
s[root2] = root1; //小树合并到大树
}else{
s[root2] += s[root1];
s[root1] = root2;
}
}
/**
* 查操作:压缩路径
* @param s
* @param x
* @return
*/
int find1(int[] s,int x){
int root = x;
while(s[root] >= 0) root = s[root]; //循环找到根节点
while (x != root){ //压缩路径
int t = s[x]; //t指向x的父节点
s[x] = root; //x直接挂到根节点下
x = t;
}
return root;
}
}
本质上表示集合的一种逻辑关系。
三. 🦁 总结
根据王道视频课总结的数据结构知识点,对于期末考、考研、面试的宝子有帮助哦!!!