定义
流形(Manifold)是一种广义的曲面概念,用于描述局部上类似于欧几里德空间的空间。简而言之,流形是一个局部与欧几里德空间同胚(homeomorphic)的空间,但并不一定是全局上同胚的。(局部同胚欧式空间是为了方便处理这种广义的曲面。)
流形空间是指一个由流形构成的空间,其中每个点都对应于流形的一个实例。
为什么要有流形?
非欧式空间难以处理,特别是涉及到曲率和奇异性等概念时,往往难以直接处理。流形的定义允许我们在局部上将复杂的几何问题转化为类似欧式空间的问题。这个局部的类似欧式空间性质为我们提供了一种简化问题的方法,使得我们可以在流形上运用欧式空间中的数学工具,从而更有效地处理问题。
流形要满足什么性质?
拓扑同胚
对于流形中的每个点P,都存在一个包含P的开集U,使得U与欧式空间中的开集V存在拓扑同胚。拓扑同胚意味着存在一个双射函数(即一一映射),它将U中的点映射到V中的点,同时保持了它们之间的拓扑关系。这个性质保证了流形的局部结构与欧式空间的局部结构是相似的。
可微结构
在流形的每个点P,都存在一个坐标图(coordinate chart),它是一个映射函数,将P附近的点映射到欧式空间中的点。这个坐标图应该是可微的,意味着它在流形上的每一点处都具有连续且可导的性质。换句话说,流形上的点应该能够用欧式空间中的坐标来表示,并且这个坐标表示应该具有光滑性。
欧式空间和流形空间的区别和联系?
区别:
基本结构:欧式空间是我们熟悉的传统三维空间,其中的点由三个实数(x、y、z)表示,具有直角坐标系。在欧式空间中,可以进行常规的线性运算和加法操作。而流形空间是一种更一般的概念,它在局部上与欧式空间同胚,但在全局范围内可能不是直角坐标系。
维度:欧式空间的维度是固定的,例如三维欧式空间就有三个坐标轴(x、y、z)。而流形空间的维度可以是任意的,取决于流形的定义。例如,SO(3)流形是三维的,而SO(2)流形是二维的。
结构:欧式空间是平直的,它遵循欧几里德几何学的性质。而流形空间通常是曲面的或具有一定的曲率,它遵循非欧几里德几何学的性质。流形空间在局部上与欧式空间类似,但在全局范围内可能有非平直的结构。
联系:
局部同胚:流形空间在局部上与欧式空间是同胚的,意味着在流形的每一点附近都存在一个局部欧式坐标系,可以将局部的流形映射到欧式空间中。这使得在流形空间上的数学运算和分析可以通过局部欧式空间进行处理。
数学工具:欧式空间中的许多数学工具和方法也可以扩展到流形空间中,尽管可能需要适应流形空间的特殊性质。例如,微积分、线性代数和向量空间等概念在流形空间中也有相应的推广。
总体而言,流形空间和欧式空间是两种不同的数学空间,它们在结构和性质上有所不同,但在一些局部性质和数学工具上存在联系。流形空间的一般性使其成为处理复杂几何问题和高维数据分析的有力工具.
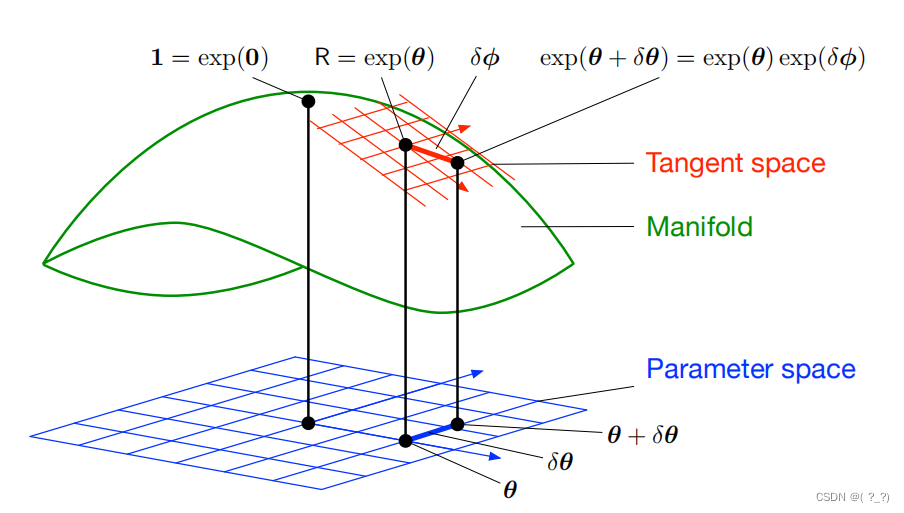
流形多种多样,以下以SO(3)流形为例:
在姿态中,旋转矩阵的李群就是一个SO(3)流形,大概的样子想象为一个三维的球体或球壳。每个球面上的点都对应着一个旋转矩阵,而球体的表面则包含了所有可能的旋转姿态。任意的两点之间都相差一个旋转矩阵。这和欧式空间中定义就完全不一样了。但是SO(3)流形有局部同胚欧式空间,也就是李代数!!!**李代数就是SO(3)流形在原点处同胚的欧式空间!**所以李群上的一些复杂操作可以转到同胚的欧式空间中,也就是李代数中!如果不在原点附近的同胚欧式空间,一般来说不再是李代数的空间。李代数仅仅是单位元处的同胚欧式空间。所以在李群中的操作,都可以使用李群欧式空间中来操作。
将姿态定义在流形上比定义在欧式空间上有什么好处?
连续性:姿态定义在流形空间中时,旋转操作的组合和插值都保持了流形的连续性。这意味着在流形空间上进行旋转操作时,不会出现突变或不连续性,从一个姿态平滑地过渡到另一个姿态。
不会出现奇异性:在流形空间上定义姿态可以避免一些奇异性问题。在欧式空间中,例如使用欧拉角时,存在万向锁问题,导致某些方向上的旋转变得不稳定。而在流形空间上,使用四元数或旋转矩阵等表示方式,可以避免这些奇异性问题,从而提高了姿态的稳定性。(欧式空间中姿态表示使用欧拉角)
避免过度参数化:姿态定义在流形空间上通常采用最小的参数化方式,例如四元数、旋转矩阵等。相比之下,在欧式空间中使用欧拉角时,可能会存在多种表示方式表示相同的旋转,导致过度参数化,增加了问题的复杂性。
保持结构特性:在流形空间上定义姿态,比如三维旋转群(SO(3)),可以保持旋转矩阵的正交性和行列式等于1的特性。这保证了旋转操作仍然是合法的旋转。
IMU的状态
IMU中的速度、位置等是定义在欧式空间中的,姿态通常是与其他状态(如速度、位置)一起进行融合。在融合过程中,需要将不同类型的状态(流形空间和欧式空间)统一起来,可能需要使用特定的算法和转换来进行集成。确保在状态融合过程中考虑到流形空间的性质,以保持状态更新的连续性和稳定性是非常重要的。此外,还需要注意数值计算的稳定性和数值误差,以避免在处理复杂状态时产生不良的结果。