Bagging方法6大面试热点问题

Q1：为什么Bagging算法的效果比单个评估器更好？

该问题其实是在考察Bagging方法降低模型泛化误差的基本原理。

泛化误差是模型在未知数据集上的误差，更低的泛化误差是所有机器学习/深度学习建模的根本目标。在机器学习当中，泛化误差一般被认为由偏差、方差和噪音构成。其中偏差是预测值与真实值之间的差异，衡量模型的精度。方差是模型在不同数据集上输出的结果的方差，衡量模型稳定性。噪音是数据收集过程当中不可避免的、与数据真实分布无关的信息。

当算法是回归算法、且模型衡量指标是MSE时，模型的泛化误差可以有如下定义：

Bagging的基本思想是借助弱评估器之间的“独立性”来降低方差，从而降低整体的泛化误差。这个思想可以被推广到任意并行使用弱分类器的算法或融合方式上，极大程度地左右了并行融合方式的实际使用结果。其中，“降低方差”指的是bagging算法输出结果的方差一定小于弱评估器输出结果的方差，因此在相同数据上，随机森林往往比单棵决策树更加稳定，也因此随机森林的泛化能力往往比单棵决策树更强。

Q2：为什么Bagging可以降低方差？

以随机森林为例，假设现在随机森林中含有𝑛个弱评估器（𝑛棵树），任意弱评估器上的输出结果是 $X_{i}$ ，则所有这些弱评估器输出结果的方差可以被表示为Var( $X_{i}$ )。假设现在我们执行回归任务，则森林的输出结果等于森林中所有树输出结果的平均值，因此森林的输出可以被表示为 $\overline{X}=\frac{\sum X_{i}}{n}$ ，因此随机森林输出结果的方差可以被表示为Var( $\overline{X}$ )，也可以写作Var（ $\frac{\sum X_{i}}{n}$ ）。在数学上很容易证明：当森林中的树互相独立时，Var( $\overline{X}$ )永远小于Var( $X_{i}$ )。证明如下：

Var(A + B) = Var(A) + Var(B)，其中A和B是相互独立的随机变量
Var(aB) = $a^{2}$ Var(B)，其中a是任意常数

假设任意树输出的方差Var( $X_{i}$ ) = $\sigma ^{2}$ ，则有：

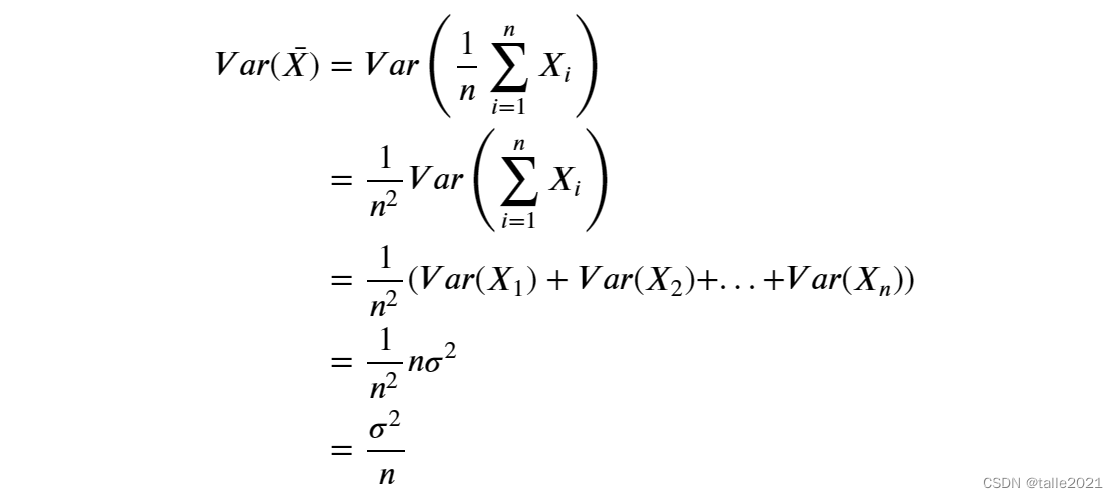
当𝑛为正整数、且弱评估器之间相互独立时，必然有Var( $\overline{X}$ )永远小于Var( $X_{i}$ )，这是随机森林的泛化能力总是强于单一决策树的根本原因。

Bagging降低方差的原理对分类同样有效，在随机森林分类器中，我们需要对每棵树上的输出结果进行少数服从多数的计算，并将“多数”指向的类别作为随机森林分类器的结果。例如：

r = np.array([-1,-1,-1, 1, 1, 1, 1]) #-1，1
(r == 1).sum() #4
(r == -1).sum() #3

按少数服从多数结果，随机森林的输出应该是1。这个过程可以很容易使用函数来替代，只要我们对所有树的结果的均值套上sigmoid函数，再以0.5为阈值就可以。

def sigmoid(z):
    return 1/(1+np.e**(-z))

r = np.array([-1,-1,-1, 1, 1, 1, 1])
r.mean() #0.14285714285714285
sigmoid(r.mean())

0.5356536708339716

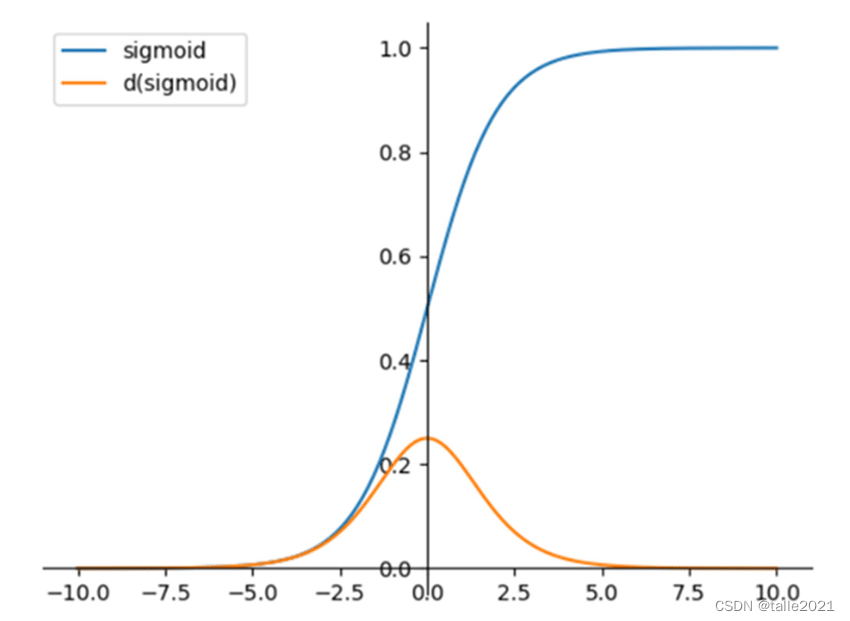
sigmoid函数的结果大于0.5，因此最终输出的类别为1。当模型效果足够好时，sigmoid函数的结果一般与少数服从多数相一致。

因此，当弱评估器的方差是Var( $X_{i}$ )时，随机森林分类器的方差可以写作Var( $f(\overline{X})$ )，其中𝑓(𝑧)就是sigmoid函数， $\overline{X}$ 是所有弱评估器的分类结果的均值。在数学上也能证明：当森林中的树互相独立，且𝑓(𝑥)为sigmoid函数时，Var( $f(\overline{X})$ )永远小于Var( $X_{i}$ )，证明如下：

当𝑓(𝑥)为二阶可导函数时，根据泰勒展开有：

Var[f(A)] ≈≈ (f'E[A]))2∗2∗Var[A]
其中A为任意随机变量，f'为函数𝑓(𝑥)的一阶导数

假设任意树输出的方差Var( $X_{i}$ ) = $\sigma ^{2}$ ，则有：

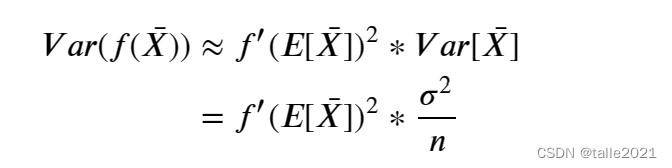
根据回归类算法的推导，我们很容易可以得到 $Var\left [ \overline{X} \right ]=\frac{\sigma ^{2}}{n}$ ，因此上式的后半部分一定是小于 $\sigma ^{2}$ 的。同时，式子的第一部分是sigmoid函数一阶导数的平方，sigmoid函数的一阶导数的取值范围为[0,0.25]，因此无论 $E\left [ \overline{X} \right ]$ 是怎样的一个值，该式子的前半部分一定是一个位于范围[0,0.0625]的数。一个小于1的数乘以 $\frac{\sigma ^{2}}{n}$ 必然会得到小于 $\sigma ^{2}$ 的数。因此Var( $f(\overline{X})$ )永远小于Var( $X_{i}$ )。相似的数学过程可以被推广至多分类，我们使用softmax函数/多对多方式来处理随机森林的结果。

Q3：Bagging有效的基本条件有哪些？Bagging的效果总是强于弱评估器吗？

Bagging能够提升模型效果的条件有以下三个：

1、弱评估器的偏差较低，特别地来说，弱分类器的准确率至少要达到50%以上
2、弱评估器之间相关性弱，最好相互独立
3、弱评估器是方差较高、不稳定的评估器

第一个条件非常容易解释。Bagging集成算法是对基评估器的预测结果进行平均或用多数表决原则来决定集成评估器的结果。在分类的例子中，假设我们建立了25棵树，对任何一个样本而言，平均或多数表决原则下，当且仅当有13棵以上的树判断错误的时候，随机森林才会判断错误。假设单独一棵决策树在样本i上的分类准确率在0.8上下浮动，那一棵树判断错误的概率大约就有0.2(ε)，那随机森林判断错误的概率（有13棵及以上的树都判断错误的概率）是：

$e_{random_forest}=\sum_{i=13}^{25}C_{25}^{i}\varepsilon ^{i}(1-\varepsilon )^{25-i}=0.000369$

import numpy as np
from scipy.special import comb

np.array([comb(25,i)*(0.2**i)*((1-0.2)**(25-i)) for i in range(13,26)]).sum()

0.00036904803455582827

可见，判断错误的几率非常小，这让随机森林的表现比单棵决策树好很多。基于上述式子，我们可以绘制出以弱分类器的误差率ε为横坐标、随机森林的误差率为纵坐标的图像：

import numpy as np
x = np.linspace(0,1,20)
y = []
for epsilon in np.linspace(0,1,20):
    E = np.array([comb(25,i)*(epsilon**i)*((1-epsilon)**(25-i)) 
                  for i in range(13,26)]).sum()
    y.append(E)
plt.plot(x,y,"o-")
plt.plot(x,x,"--",color="red")
plt.xlabel("individual estimator's error")
plt.ylabel("RandomForest's error")
plt.grid()
plt.show()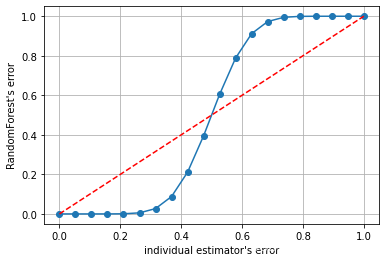

可以从图像上看出，当基分类器的误差率小于0.5，即准确率大于0.5时，集成的效果是比弱分类器要好的。相反，当基分类器的误差率大于0.5，袋装的集成算法就失效了。所以在使用随机森林之前，一定要检查，用来组成随机森林的分类树们是否都有至少50%的预测正确率。

对于第二个条件，上面已经说明了唯有弱评估器之间相互独立、弱评估器输出的结果相互独立时，方差计算公式的前提假设才能被满足，Bagging才能享受降低方差的福利。

然而在现实中，森林中的弱评估器很难完全相互独立，因为所有弱评估器都是在相同的数据上进行训练的、因此构建出的树结构也大同小异。幸运的是，我们能够衡量弱评估器之间相关性。以随机森林回归为例，假设任意弱评估器之间的相关系数为 $\rho$ ，则随机森林输出结果的方差等于：

$Var(\overline{X})=\frac{\sigma ^{2}}{n}+\frac{n-1}{n}\rho \sigma ^{2}$

这个公式是根据比奈梅定义(Bienaymé's Identity)与协方差相关的公式推导出来的，这暗示随机森林输出结果的方差与森林中弱评估器之间的相关性是负相关的，弱评估器之间的相关性越强，随机森林输出的结果的方差就越大，Bagging方法通过降低方差而获得的泛化能力就越小。因此在使用随机森林时，我们需要让弱评估器之间尽量相互独立，我们也可以通过这一点来提升随机森林的水平。

同样，因为Bagging是作用于方差的集成手段，所以Bagging方法擅长处理方差大、偏差低的模型，而不擅长处理方差小、偏差大的模型。对于任意算法而言，方差与偏差往往不可兼得，这也很容易理解——想要在当前数据集上获得低偏差，必然意味着需要重点学习当前数据集上的规律，就不可避免地会忽略未知数据集上的规律，因此在不同数据集上进行测试时，模型结果的方差往往很大。

Q4：Bagging方法可以集成决策树之外的算法吗？

强大又复杂的算法如决策树、支持向量机等，往往学习能力较强，倾向于表现为偏差低、方差高，这些算法就比较适合于Bagging。而线性回归、逻辑回归、KNN等复杂度较低的算法，学习能力较弱但表现稳定，因此倾向于表现为偏差高，方差低，就不太适合被用于Bagging。

在sklearn当中，可以使用以下类来轻松实现Bagging:

class sklearn.ensemble.BaggingRegressor(base_estimator=None, n_estimators=10, *, 
max_samples=1.0, max_features=1.0, bootstrap=True, bootstrap_features=False, 
oob_score=False, warm_start=False, n_jobs=None, random_state=None, verbose=0)

class sklearn.ensemble.BaggingClassifier(base_estimator=None, n_estimators=10, *, 
max_samples=1.0, max_features=1.0, bootstrap=True, bootstrap_features=False,
 oob_score=False, warm_start=False, n_jobs=None, random_state=None, verbose=0)

不难发现，这两个类的参数与随机森林大同小异，只不过因为弱分类器不再局限于树模型，因此不再具有对树模型进行剪枝的一系列参数。需要注意的是，这两个类只能够接受sklearn中的评估器作为弱评估器。

Q5：怎样增强Bagging中弱评估器的独立性？

在实际使用数据进行训练时，我们很难让Bagging中的弱评估器完全相互独立，主要是因为：训练的数据一致和弱评估器构建的规则一致，导致最终建立的弱评估器都大同小异，Bagging的效力无法完整发挥出来。为了弱评估器构建规则一致的问题，我们有了Averaging和Voting这样的模型融合方法：基本来看，就是使用Bagging的逻辑来融合数个不同算法的结果。而当我们不使用模型融合时，我们可以使用“随机性”来削弱弱分类器之间的联系、增强独立性、提升随机森林的效果。

在随机森林中，天生就存在有放回随机抽取样本建树的机制，因此才会有bootstrap、max_samples等参数，才会有袋外数据、袋外评估指标oob_score等属性，意在使用不同的数据建立弱评估器。除了有放回随机抽样之外，还可以使用max_features随机抽样特征进行分枝，加大弱评估器之间的区别。也正因为存在不同的随机的方式，Bagging集成方法下才有了多种不同的算法。

Q6：除了随机森林，你还知道其他Bagging算法吗？

Bagging方法的原理简单，因此Bagging算法之间的不同主要体现在随机性的不同上。在上世纪90年代，对样本抽样的bagging、对特征抽样的bagging、对样本和特征都抽样的bagging都有不同的名字，不过今天，所有这些算法都被认为是装袋法或装袋法的延展。在sklearn当中，除了随机森林之外还提供另一个bagging算法：极端随机树。极端随机树是一种比随机森林更随机、对方差降低更多的算法，我们可以通过以下两个类来实现它：

class sklearn.ensemble.ExtraTreesClassifier(n_estimators=100, *, criterion='gini', 
max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0,
max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, bootstrap=False, 
oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False,
class_weight=None, ccp_alpha=0.0, max_samples=None)

class sklearn.ensemble.ExtraTreesRegressor(n_estimators=100, *, criterion='squared_error', 
max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, 
max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, bootstrap=False, 
oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, 
ccp_alpha=0.0, max_samples=None)

与随机森林一样，极端随机树在建树时会随机挑选特征，但不同的是，随机森林会将随机挑选出的特征上每个节点都进行完整、精致的不纯度计算，然后挑选出最优节点，而极端随机树则会随机选择数个节点进行不纯度计算，然后选出这些节点中不纯度下降最多的节点。这样生长出的树比随机森林中的树更不容易过拟合，同时独立性更强，因此极端随机树可以更大程度地降低方差。当然，这种手段往往也会带来偏差的急剧下降，因此极端随机树是只适用于方差过大、非常不稳定的数据的。除非特殊情况，我们一般不会考虑使用极端随机树。