打家劫舍
- 198.打家劫舍
- 213.打家劫舍II
- 337.打家劫舍 III
198.打家劫舍
1.dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
2.dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
3.初始化,dp[0] 和 dp[1],dp[0] 一定是 nums[0],dp[1] = max(nums[0], nums[1]);
3.遍历顺序,dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历!
class Solution {
public int rob(int[] nums) {
if(nums ==null||nums.length ==0) return 0;
if(nums.length ==1) return nums[0];
int len = nums.length;
int[] dp = new int[len];
dp[0]=nums[0];
dp[1] = Math.max(nums[0],nums[1]);
for(int i =2;i<nums.length;i++){
dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]);
}
return dp[len-1];
}
}
进一步对滚动数组的空间优化 dp数组只存与计算相关的两次数据
因为当前能偷的最多与上一家还有上上一家有关
class Solution {
public int rob(int[] nums) {
if(nums.length ==1) return nums[0];
int len = nums.length;
int[] dp = new int[2];
dp[0]=nums[0]; //上上家
dp[1] = Math.max(nums[0],nums[1]); // 上一家
int res =0;
for(int i =2;i<nums.length;i++){
res = Math.max(dp[1],dp[0]+nums[i]); //当前家的最大值
dp[0] = dp[1];
dp[1] = res;
}
return dp[1];
}
}
213.打家劫舍II
这个视频讲解的不错
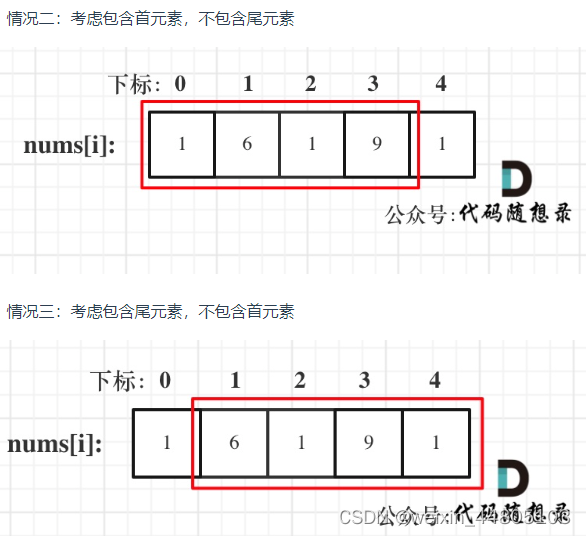
这道题与上一道不同的是首尾相连
那么第一个和最后一个一定只能选择其中一个
class Solution {
public int rob(int[] nums) {
if(nums.length == 1) return nums[0];
int n = nums.length;
int res = Math.max(robAction(Arrays.copyOfRange(nums,0,n-1)),robAction(Arrays.copyOfRange(nums,1,n)));
return res;
}
public int robAction(int [] nums){
if(nums.length ==1) return nums[0];
int[] dp = new int[2];
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
int temp =0;
for(int i=2;i<nums.length;i++){
temp = Math.max(dp[1],dp[0]+nums[i]);
dp[0] = dp[1];
dp[1] = temp;
}
return dp[1];
}
}
337.打家劫舍 III
每个节点是否被选中,取决于该节点的左右子节点是否被选
方法一:递归
从根节点开始遍历,分为两种情况,偷当前节点和孙子节点,不偷当前节点,偷孩子
再对每个结点比较大小
class Solution {
// 1.递归去偷,超时
public int rob(TreeNode root) {
if (root == null)
return 0;
int money = root.val;
if (root.left != null) {
money += rob(root.left.left) + rob(root.left.right);
}
if (root.right != null) {
money += rob(root.right.left) + rob(root.right.right);
}
return Math.max(money, rob(root.left) + rob(root.right));
}
}
上面的递归超时,因为出现了很多重复的步骤,改进记忆法递归
方法二:递归去偷,记录状态
从根节点开始遍历的时候,就用一个类似数组的集合进行存放,减少遍历次数
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
Map<TreeNode,Integer> memo = new HashMap<>();
return robAction(root,memo);
}
public int robAction(TreeNode root, Map<TreeNode,Integer> memo ){
//停止条件
if(root == null) return 0;
// 避免重复操作
if(memo.containsKey(root)){
return memo.get(root);
}
//1.选择当前节点 再偷孙子
int cur = root.val;
if(root.left !=null){
cur +=robAction(root.left.left,memo)+robAction(root.left.right,memo);
}
if(root.right != null){
cur +=robAction(root.right.left,memo) + robAction(root.right.right,memo);
}
//2.不偷当前节点,去偷孩子
int cur1 = robAction(root.left,memo)+robAction(root.right,memo);
//比较上面两种选择
int res = Math.max(cur,cur1);
memo.put(root,res);
return res;
}
}
方法三: 状态标记递归
每个节点是否选择,取决于其左右子节点(所以只需要记录临近节点的状态,其余就不用管,就像上一道里面的上一个,上上个)
dp[0],dp[1]分别表示当前节点没有被选中,和被选中
left[0],left[1]表示其左孩子没选中和选中,right同样
对于当前节点:
不偷:Max(左孩子不偷,左孩子偷) + Max(又孩子不偷,右孩子偷),我不偷,我的孩子可偷可不偷
root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +Math.max(rob(root.right)[0], rob(root.right)[1])
偷:左孩子不偷+ 右孩子不偷 + 当前节点偷,我偷,孩子必然不能偷
class Solution {
public int rob(TreeNode root) {
int[] dp = robAction(root);
return Math.max(dp[0],dp[1]);
}
public int[] robAction(TreeNode root ){
//停止条件
if(root == null) return new int[2];
int[] left = robAction(root.left);
int[] right = robAction(root.right);
int[] dp = new int[2];
dp[0] = Math.max(left[0],left[1])+Math.max(right[0],right[1]);//当前节点没有被选中
dp[1] = root.val + left[0] + right[0];//被选中
return dp;
}
}