区间预测 | MATLAB实现基于QRF随机森林分位数回归时间序列区间预测模型

news2024/10/6 10:36:36

区间预测 | MATLAB实现基于QRF随机森林分位数回归时间序列区间预测模型

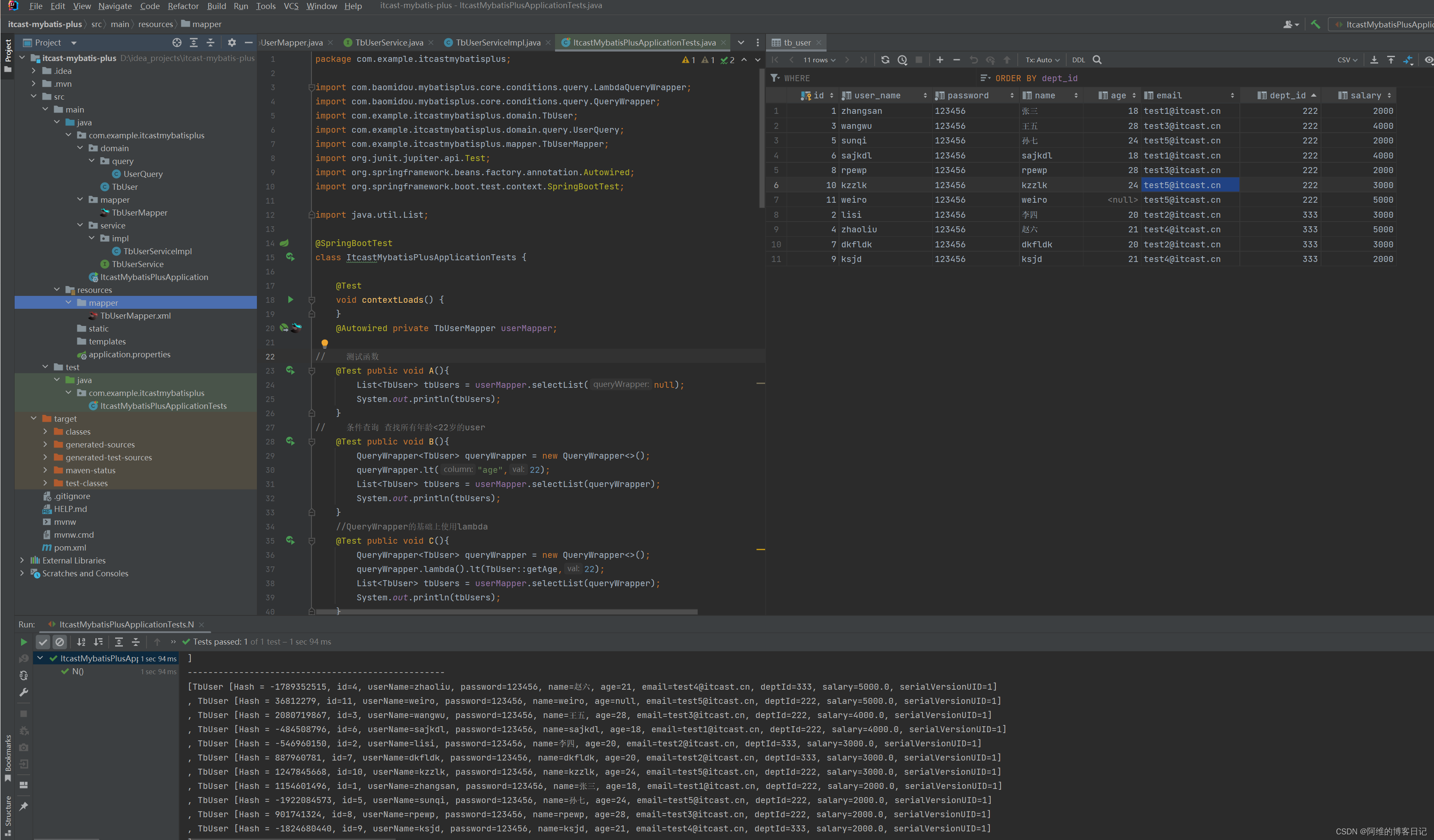
效果一览

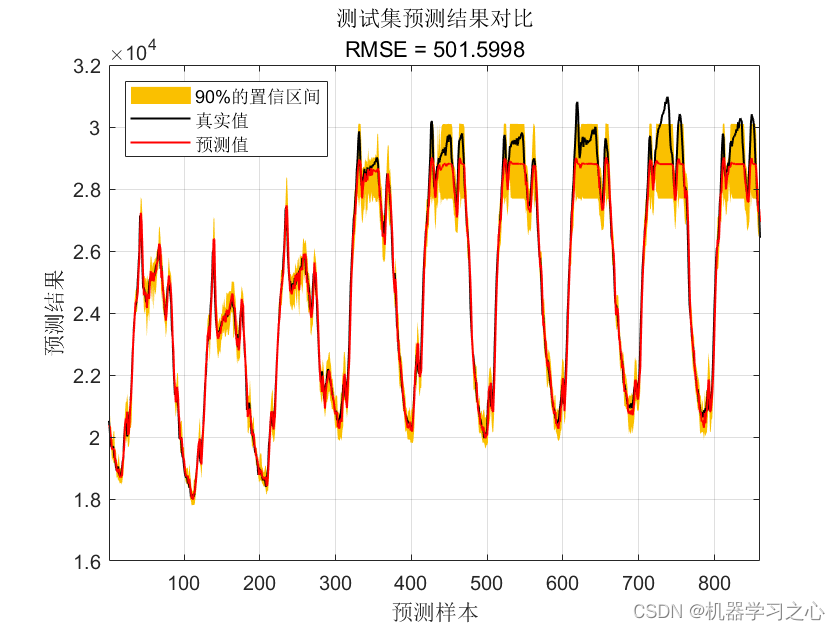
基本介绍

1.Matlab实现基于QRF随机森林分位数回归时间序列区间预测模型；
2.基于随机森林回归（QRF）分位数时间序列区间预测，Matlab代码，单变量输入模型，data为数据集（功率数据集），QRFTS为主程序，其余为函数文件，无需运行；
3.评价指标包括：R2、MAE、MAPE、MSE和区间覆盖率和区间平均宽度百分比等，代码质量极高，方便学习和替换数据；

随机森林分位数回归是一种基于随机森林过程的学习方法，用于对时间序列进行预测。在时间序列区间预测中，RF可以用于预测一系列未来时间点的分位数，从而提供关于未来趋势的一些信息。具体来说，RF可以用于估计某个时间点的观测值在给定分位数水平下的概率分布。这个分布可以用来计算区间预测。RF的预测结果可以提供一些关于未来时间序列的不确定性信息，这对于决策者和风险管理者来说非常有用。在应用 RF进行时间序列区间预测时，需要首先选择合适的高斯过程模型，然后基于历史数据进行参数估计和模型训练。一旦模型训练完成，就可以用它来对时间序列进行预测和区间估计。需要注意的是，RF是一种复杂的学习方法，需要一定的数学和计算机技能才能进行有效的应用。此外，预测结果也受到历史数据的限制，因此在进行时间序列区间预测时需要谨慎选择样本数据，并且需要不断更新模型以反映新的数据和趋势。

程序设计

完整程序和数据获取方式1：私信博主，同等价值程序兑换；
完整程序和数据下载方式2(资源处直接下载)：MATLAB实现基于QRF随机森林分位数回归时间序列区间预测模型
完整程序和数据下载方式3(订阅《RF随机森林》专栏，数据订阅后私信我获取)：MATLAB实现基于QRF随机森林分位数回归时间序列区间预测模型

%%  数据集分析
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度

%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

%%  模型创建
alpha = 0.10;
net = fitrgp(p_train, t_train);

%%  仿真测试


%%  数据反归一化
L_sim1 = mapminmax('reverse', l_sim1, ps_output);
L_sim2 = mapminmax('reverse', l_sim2, ps_output);

T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);