一)回文子串:
647. 回文子串 - 力扣(LeetCode)
思路1:暴力枚举:
for(int i=0;i<array.length;i++)
for(int j=i;j<array.length;j++)
我们的中心思路就是枚举出所有的子字符串,然后进行判断所有的子串是否是回文串
思路2:中心扩散:
我们从左向右遍历字符串中的每一个字符,遍历到某一个字符之后,我们向左向右各走一步,判断这个字符的左右两边是否相等,我们可以向左向右各走一步,如果两边不一样或者某一边走出了字符串的边界位置;
但是如果是偶数的情况,可以是选取两个字符从中间向两边进行扩展
思路3:动态规划
回文串问题是用动态规划解决可以进行判断能够将所有的子串是否是回文的信息,保存在dp表里面,dp[i][j]表示以i位置为起点,j位置为中点的子串,是否是回文串
3.1)如果array[i]!=array[j]那么从i位置到j位置的这段字符串,一定不是回文串
3.2)如果array[i]==array[j],又是分成三种情况:
if(i==j) dp[i][j]=true
else if(i+1==j) dp[i][j]=true
else dp[i][j]=dp[i+1][j-1]
进行填表的时候只是会用到上三角的值,从下向上填表,从左向右进行填表
初始化:不用初始化
填表顺序:从下向上,从左向右,因为当进行填写当前行的时候要使用到下一行的值
返回值:返回的是dp表中true的个数
class Solution { public int countSubstrings(String s) { int count=0; char[] array=s.toCharArray(); boolean[][] dp=new boolean[array.length][array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ dp[i][j]=i+1==j||i==j?true:dp[i+1][j-1]; }else{ dp[i][j]=false; } if(dp[i][j]==true) count++; } } return count; } }二)最长回文子串:
5. 最长回文子串 - 力扣(LeetCode)
class Solution { public String longestPalindrome(String s) { char[] array=s.toCharArray(); int maxlen=-1; String maxString=""; boolean[][] dp=new boolean[array.length][array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ dp[i][j]=(j==i+1||i==j)?true:dp[i+1][j-1]; if(j-i+1>=maxlen){ maxString=s.substring(i,j+1); maxlen=j-i+1; } }else{ dp[i][j]=false; } } } return maxString; } }三)回文串分割:
1745. 分割回文串 IV - 力扣(LeetCode)
暴力枚举:将所有的三元组字符串给进行枚举一下,将所有的分割出来的三个字符串给进行枚举一下,只要枚举完成,只需要将三个字符串都进行判断一下是否是回文即可
我们将整个字符串分割成三部分:
class Solution { public boolean checkPartitioning(String s) { //1.利用dp来进行检查一下所有的子串是否回文 char[] array=s.toCharArray(); boolean[][] dp=new boolean[array.length][array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ dp[i][j]=i+1==j||i==j?true:dp[i+1][j-1]; }else{ dp[i][j]=false; } } } //2.枚举第二个字符串的所有的起始位置和终止位置 for(int i=1;i<array.length;i++){//既然是枚举第二个字符串,那么前一个字符串必须得存在 for(int j=i;j<array.length-1;j++){//至少要给最后一个字符串枚举 if(dp[0][i-1]==true&&dp[i][j]==true&&dp[j+1][array.length-1]==true){ return true; } } } return false; } }
四)分割回文串:
132. 分割回文串 II - 力扣(LeetCode)
1)定义一个状态表示:
dp[i]表示以字符串i为结尾最长的子串的最少分割次数
2)根据状态标识推导状态转移方程
1)快速确定某一个字符串的子串是否是回文串
2)可以创建一个二维dp表,将所有的子串是否是回文的信息,保存到hash表里面
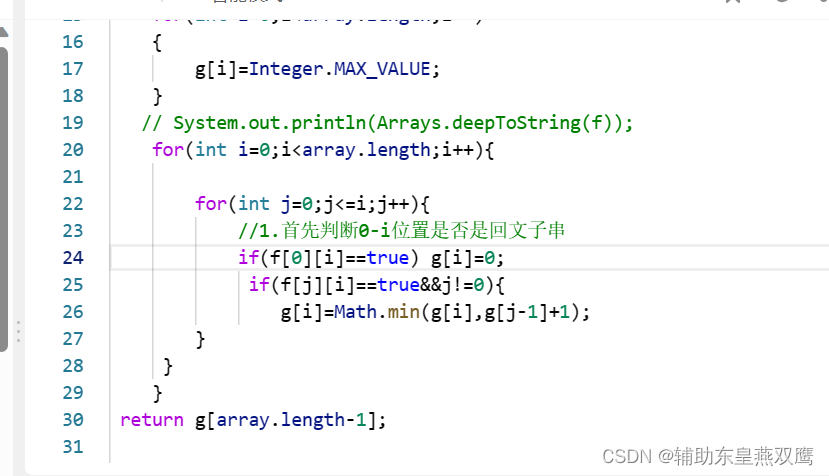
j==0的时候,0-i位置的字符传是否是回文子串已经考虑过了
j==i的时候,起始位置就是最后一个字符
如果判断f[0][i]的逻辑写到循环里面
public int minCut(String s) { char[] array=s.toCharArray(); boolean[][] f=new boolean[array.length][array.length]; int[] g=new int[array.length]; for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ f[i][j]=i==j||i+1==j?true:f[i+1][j-1]; }else{ f[i][j]=false; } } } for(int i=0;i<array.length;i++) { g[i]=Integer.MAX_VALUE; } // System.out.println(Arrays.deepToString(f)); for(int i=0;i<array.length;i++){ for(int j=1;j<=i;j++){ //1.首先判断0-i位置是否是回文子串 if(f[0][i]==true) g[i]=0; else if(f[j][i]==true){ g[i]=Math.min(g[i],g[j-1]+1); } } } return g[array.length-1]; }
上面这么写会导致进行计算f[0][0]的时候计算错误
五)最长回文子序列
516. 最长回文子序列 - 力扣(LeetCode)
一)定义一个状态表示:
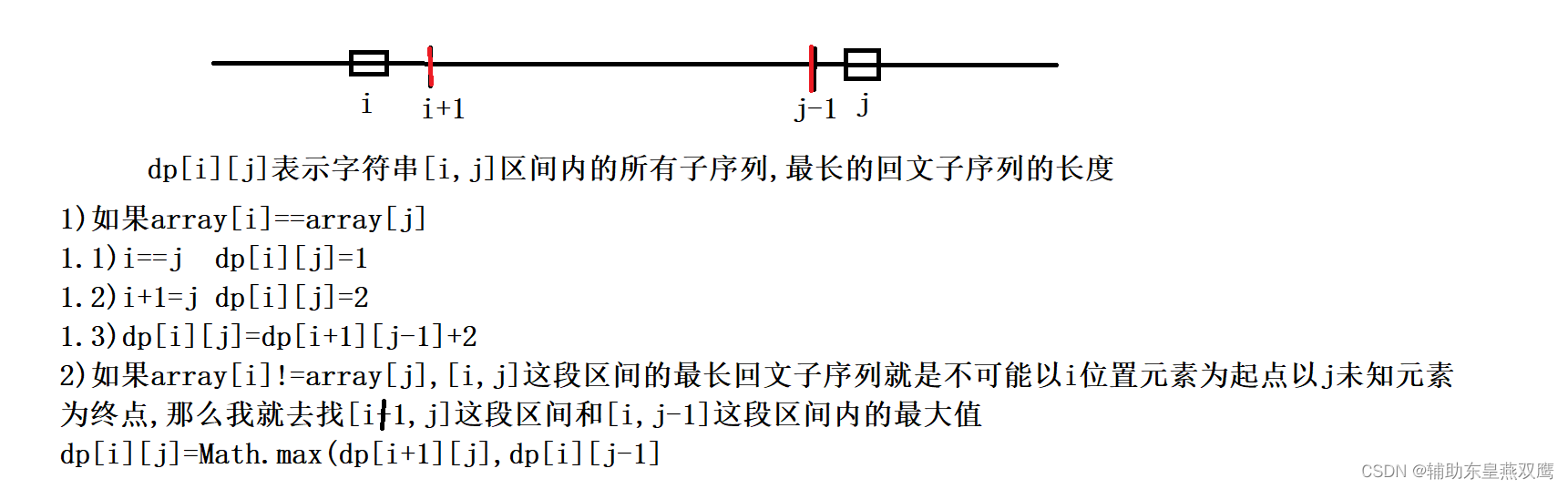
1)以i位置元素为结尾的所有子序列中最长的回文子序列的长度,如果这样定义状态标识,根本推不出状态转移方程,如果以i位置为结尾,势必就会使用到i-1,i-2等等位置的dp值来更新当前i位置的dp值,假设我们就举一个例子,dp[i-3]表示以i-3位置为结尾的最长回文子序列的长度,但是我只是知道长度,我连i位置的元素是否可以和i-3位置的元素是否能够构成回文子序列都不知道,请问我该如何更新dp[i]的值呢?是永远无法更新出最长回文子序列的长度,首先得知道是否能够成回文子序列?根本判断不出来,根本不能由前面的状态来推导出dp[i]的值,从下图所示可以看出,从[i,j]这段区间内最长回文子序列的长度可以推导出[i+1,j+1]这段区间内最长回文子序列的长度
二)根据状态标识推到状态转移方程
根据最后一个位置推导问题(i<=j)
三)初始化,填表顺序,返回值
填表顺序当进行填写dp表的时候,进行填写到dp[i][j]的时候,需要dp[i+1][j]的值,需要使用到下一行的值和dp[i][j-1]需要用到左边的值,所以填表顺序就是从下向上,从左向右
返回值:返回dp[0][array.length-1]里面的值
class Solution { public int longestPalindromeSubseq(String s) { char[] array=s.toCharArray(); //1.dp[i][j]表示以i位置为开头,j位置元素为结尾最长回文子序列的长度 int[][] dp=new int[array.length][array.length]; //2.进行填写dp表,从下向上进行填表 for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ if(i==j) dp[i][j]=1; else if(i+1==j) dp[i][j]=2; else dp[i][j]=dp[i+1][j-1]+2; }else{ dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]); } } } return dp[0][array.length-1]; } }
六)让字符串成为回文串的最少插入次数
让字符串成为回文串的最少插入次数
做回文串的题的时候,状态表示都是定义一段区间内的值
一)定义一个状态表示
dp[i][j]表示s字符串内[i,j]这段区间内的字符串使他成为回文串的最小插入次数
二)根据状态表示推导状态转移方程
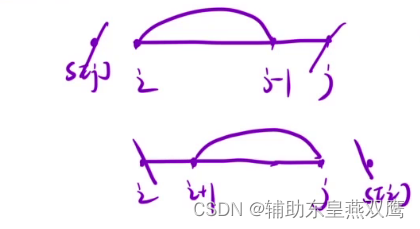
我们还是根据最近的一步划分问题
class Solution { public int minInsertions(String s) { char[] array=s.toCharArray(); int[][] dp=new int[array.length][array.length]; //1.dp[i][j]表示以i位置为起点,j位置为终点得是这段区间成为回文串得最小插入次数 for(int i=array.length-1;i>=0;i--){ for(int j=i;j<array.length;j++){ if(array[i]==array[j]){ if(i==j) dp[i][j]=0; else if(i+1==j) dp[i][j]=0; else dp[i][j]=dp[i+1][j-1]; }else{ dp[i][j]=Math.min(dp[i+1][j]+1,dp[i][j-1]+1); } } } return dp[0][array.length-1]; } }