4 微积分

4.1 导数和微分

知道概念和性质就可以过

4.2 偏导数

知道概念和性质就可以过

4.3 梯度

连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度向量。关于概念和规则如下：

推导都很容易

4.4 链式法则

上面的方法可能难以找到梯度，因为深度学习中的多元函数通常是复合的，但链式法则可以以用来微分复合函数，推导如下，其实也都学过的：

5 自动微分

求导当然简单，但是对于复杂的模型，收工更新是很痛苦的事情。
深度学习框架通过自动计算导数，即自动微分来加快求导。实际上，根据设计好的模型，系统会构建一个计算图，来跟踪计算是哪些数据通过哪些操作组合起来产生输出。自动微分使系统能够随后反向传播梯度。反向传播意味着跟踪整个计算图，填充每个参数的偏导数

5.1 简单例子

对函数y=2x^Tx关于列向量x求导：

import torch

x = torch.arange(4.0)
# 不要在每次对一个参数求导时都分配新内存
# 通过调用requires_grad_来为一个张量的梯度分配内存
x.requires_grad_(True)
# 可使用x.grad访问，默认全0

# 计算y
y = 2 * torch.dot(x, x)

#  接下来，通过调用反向传播函数来自动计算y关于x每个分量的梯度，并打印这些梯度。
y.backward()
print(x.grad)

# 上述输出结果为tensor([ 0.,  4.,  8., 12.])，则其关于x的梯度为4x
# 可以验证：
print(x.grad == 4*x)

# 现在计算x的求和函数
x.grad.zero_() # 默认情况下pytorch会累积梯度，需清除之前的值
y = x.sum()
y.backward()
print(x.grad)

结果：

tensor([ 0.,  4.,  8., 12.])
tensor([True, True, True, True])
tensor([1., 1., 1., 1.])

5.2 非标量变量的反向传播

当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。对于高阶和高维的y、x，求导结果可以是一个高阶张量。
当调用向量的反向计算时，常会计算一批训练样本中每个组成部分的损失函数的导数。这里的目的不是计算微分矩阵，而是单独计算批量中每个样本的偏导数之和。

import torch

x = torch.arange(4.0)
x.requires_grad_(True)
# 对非标量调用backward需要传入一个gradient参数，该参数指定微分函数关于self的梯度
# 这里只想求偏导数的和，所以传递一个1的梯度是合适的
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
print(x.grad)

结果：
tensor([0., 2., 4., 6.])
看到这里如果懵了记得把矩阵/向量的点积和乘积的概念搞好，推导都是很容易的

5.3 分离计算

这里希望你把我们要计算偏导的时候，所谓用到的计算图的概念给搞懂，其实就和高数里面的概念差不多，只是计算图会把它画的跟个树似的
有时希望将某些计算移动到记录的计算图之外。例如：y是关于x的函数，而z是作为y和x的函数。这时候如果要计算z关于x的梯度，由于某种原因，希望将y视为常数，且只考虑x在y被计算后发挥的作用。
直接看例子：

import torch

x = torch.arange(4.0)
x.requires_grad_(True)
# 这里可以分离y来返回一个新变量u，u与y有相同值，但丢弃计算图中如何计算y的任何信息
# 也就是说，梯度不会向后流经u到x
# 下面的计算z=u * x关于x的偏导，将u作为常数处理，而不是z=x*x*x关于x的偏导
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
print(x.grad == u)

# 由于记录了y的计算结果，现在可以在y上调用反向传播，得到y=x*x关于x的导数
x.grad.zero_()  # 这一步不要忘记了
y.sum().backward()
print(x.grad == 2 * x)

结果：

tensor([True, True, True, True])
tensor([True, True, True, True])

5.4 Python控制流的梯度计算

使用自动微分的好处就在这，即使构建函数的计算图要通过控制流，仍可以得到变量梯度：

import torch

def f(a):
    b = a * 2
    while a.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c


# 计算梯度
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

# 根据上述f函数，可得f(a)=k*a，因此可用d/a验证梯度是否正确
print(a.grad == d / a)

结果：
tensor(True)

6 概率

6.1 基本概率论

最常见的例子：掷骰子。
大数定律：随着测试次数增加，事件概率的估计值（事件出现次数/总次数）越来越接近真实的潜在概率
抽样：从概率分布中抽取样本（分布就先看成对事件的概率分配）
现在来进行验证，大家可以先搞懂Multinomial（分布式）函数：
Pytorch中的多项分布multinomial.Multinomial().sample()解析

import torch
from torch.distributions import multinomial
from d2l import torch as d2l

# 抽取一个掷骰子的样本，只需传入一个概率向量，输出的是另一个相同长度的向量：
# 它在索引i处的值是采样结果中i出现的次数
fair_probs = torch.ones([6])/6  # tensor([0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.1667])
# 进行一次抽样
print(multinomial.Multinomial(1, fair_probs).sample())
# 进行十次抽样
print(multinomial.Multinomial(10, fair_probs).sample())
# 进行1000次抽样并计算相对频率，作为真实概率的估计：
counts = multinomial.Multinomial(1000, fair_probs).sample()
print(counts / 1000)

结果：

tensor([1., 0., 0., 0., 0., 0.])
tensor([2., 1., 2., 2., 1., 2.])
tensor([0.1670, 0.1540, 0.1780, 0.1600, 0.1700, 0.1710])

可以看出，前两个输出结果中的数字和为取样数；最后一个输出结果可以证明大数定律
我们也可以看到这些概率如何随着时间的推移收敛到真实概率。 让我们进行500组实验，每组抽取10个样本：

import torch
from torch.distributions import multinomial
from d2l import torch as d2l
fair_probs = torch.ones([6])/6
counts = multinomial.Multinomial(10, fair_probs).sample((500,))  # sample指定抽样次数，默认是1次
# print(counts)
cum_counts = counts.cumsum(dim=0)  # 计算行前缀和，即sum[i][j]=a[1][j]+a[2][j]+...+a[i][j]，方便直观验证大数定律
# print(cum_counts)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)  # 每个行前缀和都除以当前行的和，以得到概率估计
d2l.set_figsize((6, 4.5))
for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),
                 label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend()
d2l.plt.show()

结果：

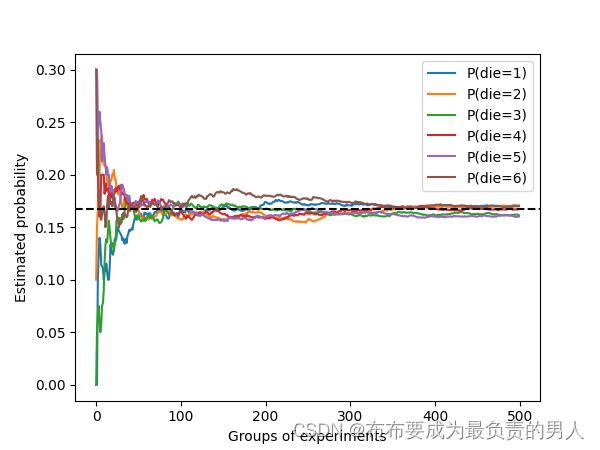
每条直线对应于骰子的6个值中的一个，并给出骰子在每组实验后出现值的估计概率。数据越多，越向真实概率收敛

6.1.1 概率论公理

6.2 处理多个随机变量

举个例子，图像包含数百万像素，因此有数百万个随机变量，可将所有元数据视为随机变量，例如位置、时间、光圈和相机类型。

6.2.1 联合概率

P(A=a,B=b)表示A=a、B=b同时满足的概率，P(A=a,B=b)<=P(A=a)。

6.2.2 条件概率

根据联合概率的不等式可以推导出：
$$0<=\frac{P(A=a,B=b)}{P(A=a)}<=1$$
我们称这个比率为条件概率，记为P(B=b|A=a)，表示：前提A=a已发生时，B=b的概率

6.2.3 贝叶斯定理

很重要的定理，根据乘法法则我们可以得到：
$$P(AB)=P(B|A)P(A)$$
根据对称性，我们可以得到：
$$P(AB)=P(A|B)(B)$$
假设P(B)＞0，则：
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

6.2.4 边际化

根据求和法则，得：B的概率相当于计算A的所有可能选择，并将所有联合概率聚合在一起：
$$P(B)=\sum _{A}P(AB)$$
这也称为边际化，其结果概率为边际概率，结果分布为边际分布

6.2.5 独立性

当事件A、B无关时：
$$P(A|B)=\frac{P(A,B)}{P(B)}=P(A)$$
同样，给定一个随机变量C，则A、B是条件独立的，当且仅当：
$$P(AB|C)=P(A|C)(B|C)$$

6.3 期望与方差

期望
1、一个随机变量X的期望：
$$E[X]=\sum _{x}xP(X=x)$$
2、函数f(x)的输入是从分布P中抽取的随机变量时，f(x)的期望值为
$$E_{xp}[f(x)]=\sum _{x}f(x)P(x)$$
方差
$$Var[x]=E[(X-E[X]{)}^2]=E[X^2]-E[X{]}^2$$

7 查阅文档

7.1 查找模块中的所有函数和类

调用dir函数，例如查询随机数生成模块中的所有属性：

print(dir(torch.distributions))

7.2 查找特定函数和类的用法

help(touch.ones)