查找：

1.二分查找：先定一个大范围，想一个数，看是在起始范围到中间范围还是中间范围到结束范围，依次循环直到确定值（相当于一直把范围折半，直到找到）

while(low<=high)
{
    int mid=(low+high)/2
    
    if(key==arr[mid])//如果值就是范围的中间值就直接输出
    else if(key>arr[mid])
    {
       low=mid+1;     
    }
    else
    {
        high=mid-1;    
    }
}

哈希表：

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

散列函数：

直接定址法：取关键字或关键字的某个线性函数值为哈希地址的方法

数字分析法：通过分析取关键字的若干数位组成哈希地址的方法

平方取中法：取关键字平方后的中间几位数组成哈希地址的方法

除留余数法：取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址的方法

H(key)=key MOD p (p<m)

哈希表表长m： 数组长度除以3/4

p:p一般取不大于表长m的最大质数 

随机数法：使用随机函数random构建哈希函数

哈希冲突

哈希冲突：不同关键字通过哈希函数映射在同一个存储位置

开放定址法：线性探测法、二次探测法、伪随机探测法

再哈希法、链地址法、建立公共溢出区

递归

1.直接递归：函数自己调用自己的方式

2.间接递归：多个函数之间相互调用

3,死递归：类似于死循环

4，递归：递归出口/递归边界 、递归前进段/递归公式

实现阶乘：

int rec(int n)
{
    if(n==0)
        return 1;
    else
        return n*rec(n-1);
}

实现斐波那契：

int Feiboncii(int n)
{
    if(n==1||n==2)
        return 2;
    else
        return Feiboncii(n-2)+Feiboncii(n-1);
}

树：

1>树：是由根结点和若干棵子树构成的树形结构

1.是n(n>=0)个结点的有限集，n>0时有且只有一个根结点，除根结点外，其余结点构成的互不相交的集合仍是一棵树

2> 空树：不含任何结点的树n=0

3>根结点：只有一个结点n=1

4> 普通树n>1: 多个结点

4.1有序树：有序树【从上到下，从左到右】是树中每棵子树从左到右排列有一定顺序，不能互换的树

4.2>无序树：无序树是树中每棵子树从左到右排列无顺序，能互换的树

4.3>子树：是树中一个结点以及其下面所有的结点构成的树

树的类型：

1>结点：树中的数据元素

2>结点的度：结点含有子树的个数

3> 根结点：没有双亲结点【前驱】的结点

4>分支结点（内部结点）：是度不为0的结点

5>叶结点（终端结点）：是度为0的结点

6>结点的层数：是从根结点到某结点所路径上的层数【根结点表示第一层】

7>树的深度(高度)：是树中所有结点层数的最大值

8>树的度：各结点度的最大值

结点之间的关系

1>父结点：是指当前结点的直接上级结点

2>孩子结点：是指当前结点的直接下级结点

3>兄弟结点：是由相同父结点的结点

4>祖先结点：是当前结点的直接及间接上级结点

5>子孙结点：是当前结点直接及间接下级结点

6>堂兄弟结点：是父结点在同一层的结点

森林

森林：是指0个或多个互不相交树的集合

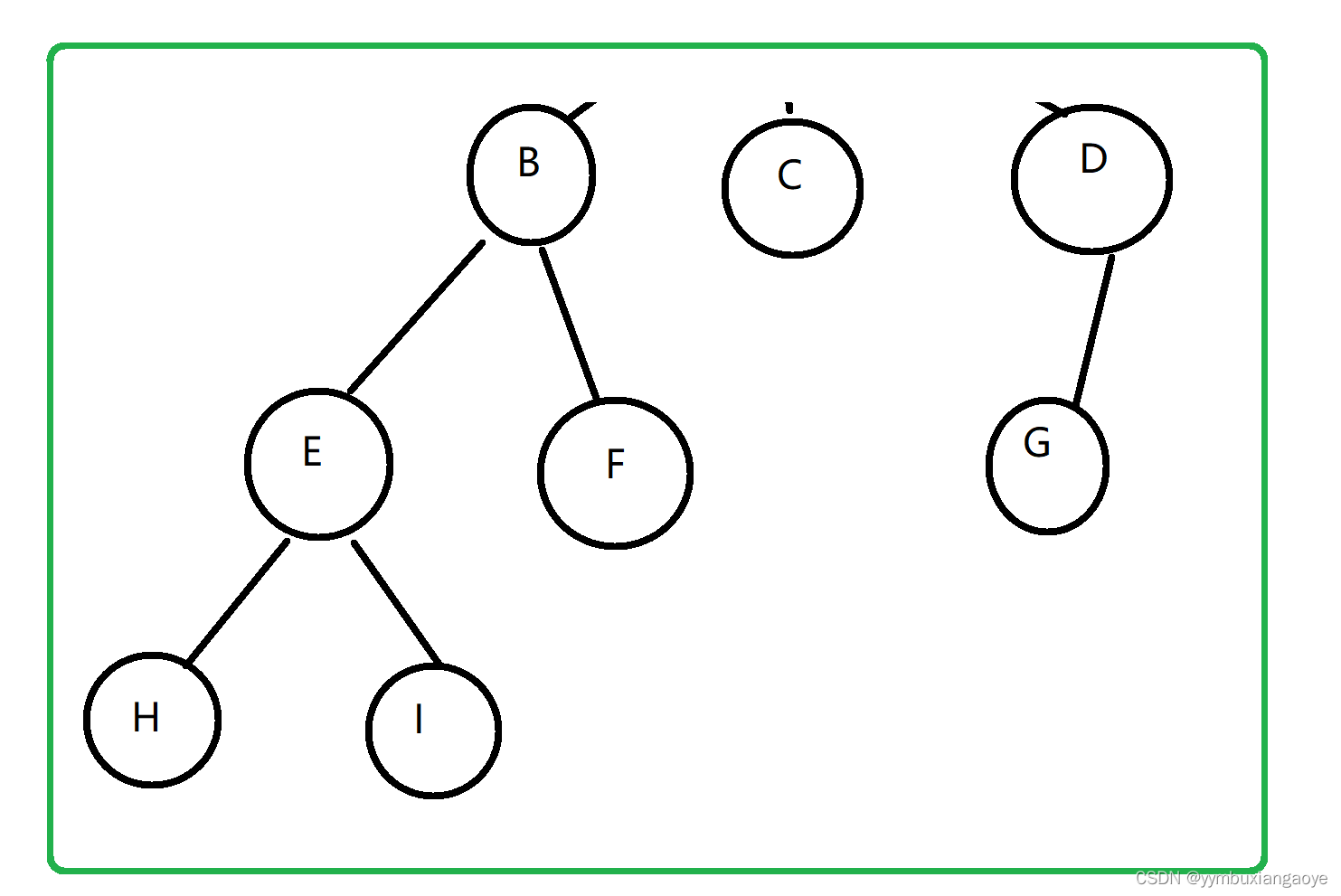
二叉树：

二叉树：树的度小于等于2

1>二叉树是每个结点最多有左、右两棵子树且严格区分顺序的树形结构【二叉树不可以互换】

2>二叉树的左边：左子树是以当前结点的左孩子结点作为根节点的子树

3>二叉树的右边：右子树是以当前结点的右孩子结点作为根节点的子树

 特殊形态：

1>空二叉树

2>只有一个根节点

3>只有左子树

4>只有右子树

5>既有左子树又有右子树

二叉树的类型

1>空二叉树：空二叉树是没有结点的二叉树

2>斜树：斜树是所有的结点都只有左子树或者都只有右子树的二叉树

2.1 左斜树：左斜树是所有的结点都只有左子树的斜树

2.2右斜树：右斜树是所有的结点都只有右子树的斜树

3>满二叉树：满二叉树是最后一层是叶子结点，其余结点度是2的二叉树

(1)叶子结点只能出现在最下面一层

(2)非叶子结点的度数一定是2

(3)同样深度的二叉树中，满二叉树的结点的个数最多，叶子结点最多

4>完全二叉树：完全二叉树是在一棵满二叉树基础上自左向右连续增加叶子结点得到的二叉树

（1）只有最后两层有叶子结点

（2）除最后一层是一棵满二叉树

（3）最后一层的叶子结点集中在左边连续的位置

二叉树的性质：

1.在非空二叉树的第i层上，至多有2^(i-1)个结点(i>=1)

2.在深度为K的二叉树上总结点最多有(2^k)-1个结点（k>=1)

3.在任意一棵二叉树中，叶子结点的数目比度数为2的结点的数目多1

4.

5.完全二叉树结点的编号方法是从上到下，从左到右根节点为1号结点设完全二叉树的结点数为n，某结点编号为I

若 i=1，则该结点是二叉树的根，无双亲，否则，其双亲结点是编号为 i/2的结点

若 2*i>n，则该结点无左孩子，否则，其左孩子结点是编号为 2i 的结点

若 2*i+1>n，则该结点无右孩子结点，否则，其右孩子结点是编号为2i+1 的结点

二叉树遍历

先序遍历：按照根左右的顺序

中序遍历：按照左根右的顺序

后序遍历：按照左右根的顺序

先序从前往后确定根，后序从后往前确定根，中序确定根左右的子树

二叉树创建：

Btree create_tree()
{
    datatypr e;
    scanf(" %c",&e);
    if(e=='#')
        return NULL;
    Btree tree=(Btree)malloc(sizeof(struct Node));
    if(tree==NULL)
        return NULL;
    tree->data=e;
    tree->lchild=create_tree();
    tree->rchild=create_tree();
    return tree;
}

先序/中序/后序遍历（依据跟的输出语句的位置）

先序（根左右）：

void outout(Btree tree)
{
    if(tree==NULL)
    return;
    printf("%c\t",tree->data);//先进来输出节点的值
    output(tree->lchild);//用递归一直输出左孩子的左孩子，直到NULL，执行下一语句；
    output(tree->rchild);//接着上一句语句，输出右孩子，如果是NULL，则返回上一节点；
}
    

中序（左根右）：

void outout(Btree tree)
{
    if(tree==NULL)
    return;
    output(tree->lchild);//用递归一直输出左孩子的左孩子，直到NULL，执行下一语句；
    printf("%c\t",tree->data);//先进来输出节点的值
    output(tree->rchild);//接着上一句语句，输出右孩子，如果是NULL，则返回上一节点；
}
  

 后序（左右根）

void outout(Btree tree)
{
    if(tree==NULL)
    return;
    output(tree->lchild);//用递归一直输出左孩子的左孩子，直到NULL，执行下一语句；
    output(tree->rchild);//接着上一句语句，输出右孩子，如果是NULL，则返回上一节点；
    printf("%c\t",tree->data);//输出节点的值
}
  

计算节点个数（0度的节点n0,1度的节点n1,和2度的节点n2）

void Count(Btree tree,int *n0,int *n1,int *n2)
{
    if(tree==NULL)
    return;
    
    if(tree->lchild==NULL && tree->rchild==NULL)
    (*n0)++;//没有子树的度为0的节点个数
    else if(tree->lchild!=NULL && tree->rchild!=NULL)
    (*n2)++;//有两个子树的度为2的节点个数
    else
    (*n1)++;//只有一个子树的度为1的节点个数
    Count(tree->lchild,n0,n1,n2);
    Count(tree->rchild,n0,n1,n2);
}

计算树的深度：

int High(Btree tree)
{
    if(tree==NULL)
        return 0;

    int left=High(tree->lchild)+1;//左子树深度
    int right=High(tree->rchild)+1;//右子树深度
    return left>right?left:right;//只算最深的子树深度
}

释放二叉树：

void free_space(Btree tree)
{
    if(tree==NULL)
        return ;

    free_space(tree->lchild);
    free_space(tree->rchild);
    free(tree);
    tree=NULL;
}