一)最长公共子序列:
1143. 最长公共子序列 - 力扣(LeetCode)
一)定义一个状态表示:根据经验+题目要求
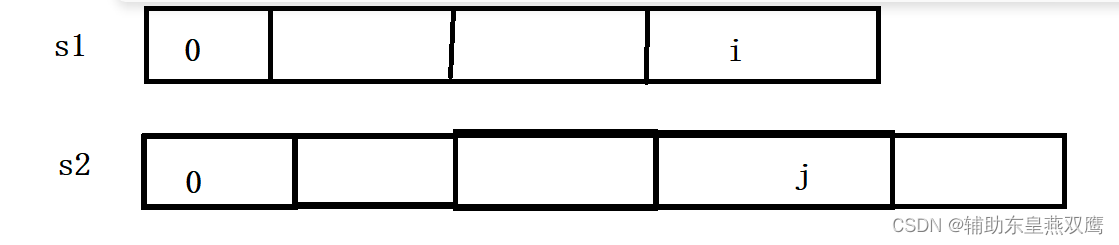
1)选取第一个字符串[0,i]区间以及第二个字符串[0,j]区间作为研究对象,先选取两段区间研究问题,先求出[0,i]中所有的子序列和[0,j]中所有的子序列,然后求出两个子序列中相同的最大的哪一个,找到最长公共子序列的长度;
2)根据题目要求来确定一个状态表示
dp[i][j]就表示s1字符串的[0,i]区间以及s2的[0,j]区间内的所有子序列中(可以包含包含以i,j为结尾,也可以不包含i,j),找到其中的最长的公共子序列的长度
二)根据状态表示推导状态转移方程:根据最后一个位置的状况来进行划分情况去讨论
如果这两个字符串的最后一个位置的字符相等,那么这两个字符串的最长公共子序列,一定是一这两个字符为结尾的,下面是用反证法来进行证明一下:
所以就可以根据这个最后一个字符的状态,分类讨论:
1)if(s1[i]==s2[j]) dp[i][j]=dp[i-1][j-1]+1
2)如果这两个字符不相等,那么最长公共子序列一定不是以这两个字符结尾的
s1[0,i]和s2[0,j-1]
s1[0,i-1],s2[0,j]
s1[0,i-1]和s2[0,j-1]
但是仔细分析之后我们发现,第一种情况已经包含了第三种情况,第二种情况也是已经包含了第三种情况,但是我们此时求的是长度,只需要保证不漏就可以了,如果求的是个数,那么这个状态表示就出现问题了
三)初始化:
1)关于字符串的dp问题,空字符串是有研究意义的,子序列是一个空串那么也是一个公共子序列,引入空串的概念,会方便初始化
2)当i==0或者是j==0的时候,也就是当进行研究第一个字符的时候,dp[i-1]和dp[j-1]会越界,在上面和右边多增加一列,这时,当i==0的时候,第一个字符串是空,当j==0的时候,第二个字符串是空,此时dp表新增加的列里面的值全部是初始化成0;
3)添加辅助节点的时候,里面的值要保证我们后续进行填表的时候是正确的,还需要注意下标的映射关系,可以不在填表的时候进行处理,而是可以在所有的字符串前面加上一个空串,这样就可以不用计算下标的映射关系了

四)填表顺序+返回值:从上向下填写每一行,每一行填写从左向右dp[m][n]
class Solution { public int longestCommonSubsequence(String text1, String text2) { int m=text1.length(); int n=text2.length(); char[] array1=text1.toCharArray(); char[] array2=text2.toCharArray(); int[][] dp=new int[m+1][n+1]; for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ if(array1[i-1]==array2[j-1]) dp[i][j]=dp[i-1][j-1]+1; else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]); } } return dp[m][n]; } }
二)不相交的线
求的是最长公共子序列
1035. 不相交的线 - 力扣(LeetCode)
dp[i][j]表示n1里面的[0,i]区间内以及n2里面的[0,j]区间内的所有子序列中,数组最长公共子序列的长度
class Solution { public int maxUncrossedLines(int[] nums1, int[] nums2) { int m=nums1.length; int n=nums2.length; int[][] dp=new int[m+1][n+1]; for(int i=1;i<=m;i++){ for(int j=1;j<=n;j++){ if(nums1[i-1]==nums2[j-1]){ dp[i][j]=dp[i-1][j-1]+1; }else{ dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]); } } } return dp[m][n]; } }
三)不同的子序列
115. 不同的子序列 - 力扣(LeetCode)
一)定义一个状态表示:
两个字符串的dp表示:dp[i][j]表示从[0,i]位置的t子串在s从[0,j]的子序列中出现的个数
dp[i][j]表示s字符串[0,j]区间内的所有子序列中,有多少个t[0,i]区间内的子串,子串是连续的,但是子序列是不连续的
二)根据状态表示推导状态转移方程:
1)我们可以将s从[0,j]这段字符串的子序列分成两类,就是根据最后一个位置的元素进行划分问题,我们目标是在s的子序列中看看有多少个t字符串
首先求出所有子序列,在求出有多少子序列中等于t
2)可以根据s的子序列中的最后一个位置是否包含j来进行划分问题,s的子序列分成两类
2.1)如果s的子序列中,最后一个位置包含s[j],if(array[i]==array[j]) dp[i][j]=dp[i-1][j-1]
2.2)如果s的子序列中,最后一个位置不包含s[j],dp[i][j]=dp[i][j-1]
我们要找的是[0,i]位置的子串在[0,j]区间内的子序列出现的个数
dp[i][j]就是上面两种情况的的总和
三)初始化+填表顺序+返回值:
3.1)因为有可能使用到i-1和j-1的值,那么我们给dp表新增加一行和一列
3.2)我们下标从1位置和1位置开始,也就是从第一个字符开始进行研究问题
3.3)细节问题:
1)引入空串
2)保证里面的值要保证后面的填表的顺序是正确的
3)还需要注意下表的映射关系:不做任何处理只是在进行填写dp表的时候下标统一进行-1即可
或者是加上在原来的字符串里面加上一个空字符即可
4)当i等于0的时候,说明t字符串是一个空串,那么无论此时j的值等于多少,s的子序列中一定是包含一个空串的,那么所有的dp[0][j]=1
5)那么当j等于0的时候,说明s没有任何子序列,s是一个空串,那么除了i等于0的时候
dp[i][0]都等于0,当i==1的时候,dp[i][0]=1
初始化:从上向下填写每一行,每一行从左向右
返回值:dp[m][n]
class Solution { public int numDistinct(String s, String t) { char[] array1=t.toCharArray(); char[] array2=s.toCharArray(); int[][] dp=new int[array1.length+1][array2.length+1]; for(int i=0;i<=array2.length;i++){ dp[0][i]=1; } for(int j=1;j<=array1.length;j++){ dp[j][0]=0; } for(int i=1;i<=array1.length;i++){ for(int j=1;j<=array2.length;j++){ //1.如果以j为结尾的子序列包含j,况且array1[i]==array2[j] if(array1[i-1]==array2[j-1]){ dp[i][j]=dp[i-1][j-1]; } //2.如果以j为结尾的子序列不包含j, dp[i][j]+=dp[i][j-1]; } } System.out.println(Arrays.deepToString(dp)); return dp[array1.length][array2.length]; } }
四)通配符匹配
44. 通配符匹配 - 力扣(LeetCode)
五)最长公共前缀:
一)定义一个状态表示:dp[i]表示以i位置为结尾的字符串数组的最长公共前缀
二)根据状态表示状态转移方程:
1)根据最近的一步来进行划分问题,如果发现这个字符串所有的i位置的元素都是相等的,那么最长公共前缀就是dp[i-1]+"ch",但是如果出现了abcde和hhhhe这种情况,如果发现以i-1位置为结尾的最长公共公共前缀是空,那么dp[i]也是空,虽然相等但是没有最长公共前缀
2)如果发现各个字符串在i位置的元素不是全部都相等,那么直接返回dp[i-1]的值
class Solution { public String longestCommonPrefix(String[] strs) { //dp[i]表示以i位置为结尾字符串数组的最长公共前缀 String minString=strs[0]; for(String str:strs){ if(minString.length()>=str.length()) minString=str; } if(minString.equals("")) return ""; //1.先进行初始化 String[] dp=new String[minString.length()]; char ch=strs[0].charAt(0); dp[0]=ch+""; for(String str:strs){ if(str.charAt(0)!=ch){ dp[0]=""; break; } } //2.进行填表 for(int i=1;i<minString.length();i++){ ch=minString.charAt(i); for(int j=0;j<strs.length;j++){ if(strs[j].charAt(i)!=ch){ return dp[i-1]; } } if(!dp[i-1].equals("")) dp[i]=dp[i-1]+ch; else dp[i]=""; } return dp[minString.length()-1]; } }