前言

在上一期征服FarmerJohn（一）三角形【USACO2020FEB-B】结束之后，我们来看一道难度有所提升的DP问题，也就是常说的动态规划，今天我们就一起解开这道动规题目。

题目内容

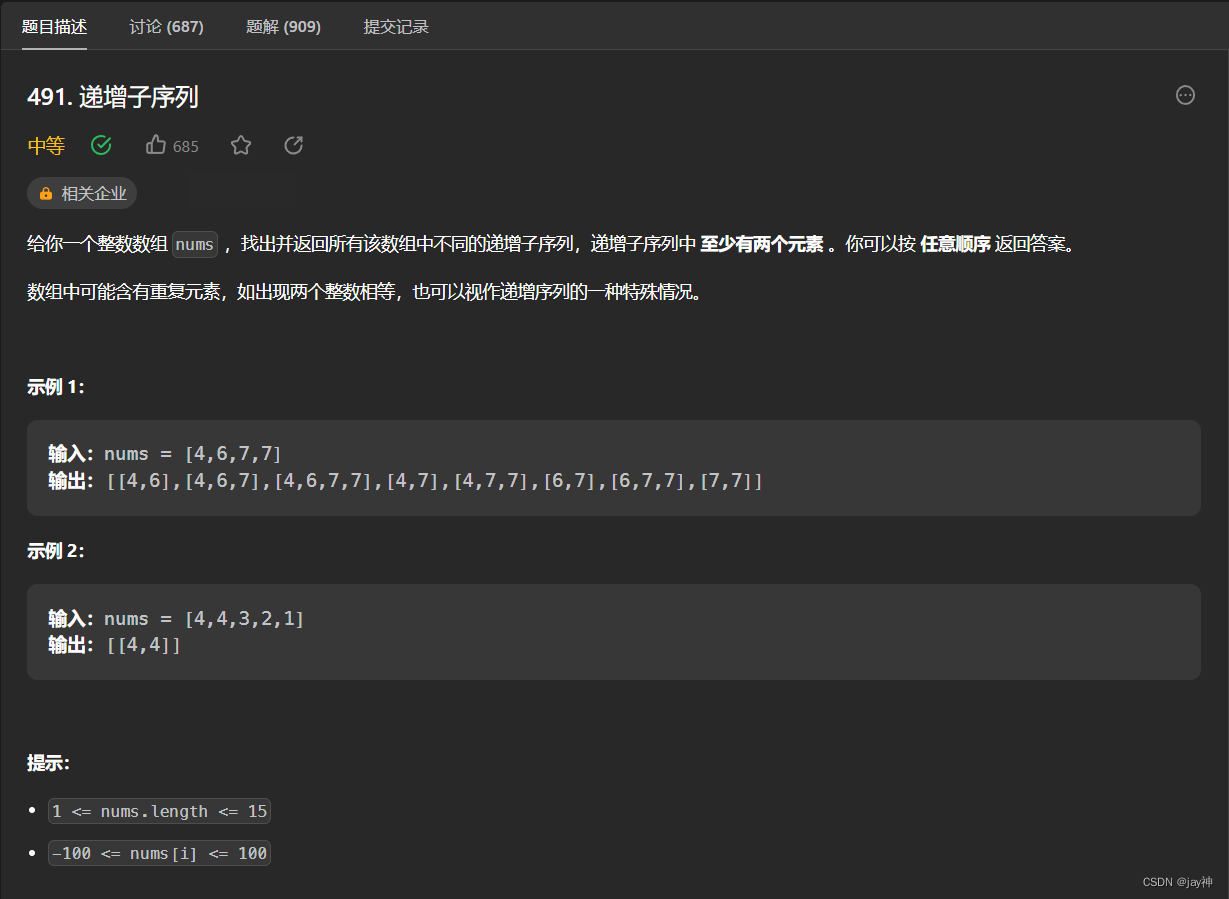
题目描述

Bessie是一只非常缺觉的奶牛．她的一天被平均分割成N段（3≤N≤3830），但是她要用其中的 B 段时间（2≤B<N）睡觉。每段时间都有一个体力恢复值 U_i（0≤U≤2×10^5），只有这段时间她在睡觉，才会获得恢复值。有了闹钟的帮助，贝茜可以选择任意的时间入睡，当然，她只能在时间划分的边界处入睡、醒来。贝茜想使所有睡觉效用的总和最大。不幸的是，每一段睡眠的第一个时间阶段都是“入睡”阶段，不记入效用值。时间阶段是不断循环的圆（一天一天是循环的嘛），假如贝茜在时间段N和时间段1睡觉，那么她将得到时间段1的恢复值。（提醒：此处的N->1，可以理解为Bessie将N->N-1作为它的一天。）

输入格式
第1行：两个用空格分隔的整数N和B，含义见题目描述。

第2到N+1行：每行一个整数，其中第i+1行的整数表示第i个时间段的恢复值。

输出格式
一行：一个整数，表示Bessie每天可以获得最大恢复值之和。
这道题可以用动态规划来解决。

输入输出样例

题目思路

这道题目可以用动态规划解决。dp状态表示为 $d p [i] [j] [k]$ ，表示考虑前 $i$ 段时间，其中睡觉的时间段为 $j$ ，而 $k$ 表示第 $i$ 段时间是否要睡觉。

dp转移方程：

$d p [i] [j] [0] = ma x (d p [i - 1] [j] [0], d p [i - 1] [j] [1])$

表示第 $i$ 段时间不睡觉，则可选择从前一段时间的不睡觉状态转移。

$d p [i] [j] [1] = ma x (d p [i - 1] [j - 1] [0], d p [i - 1] [j - 1] [1] + v a l [i])$

表示第 $i$ 段时间睡觉，则可从前一段时间不睡觉状态或睡觉状态转移，同时需要加上当前时间段的恢复值。

因为这是一个循环时间段，所以需要考虑在第 $1$ 段时间和第 $N$ 段时间之间选择一段时间进行睡觉，计算第 $1$ 段时间和第 $N$ 段时间的情况即可。

具体实现过程如下：

首先考虑第 $1$ 段时间和第 $N$ 段时间之间不睡觉的情况，然后计算最大恢复值之和。这时候需要注意第 $1$ 段时间被算作非睡觉，因此需要从 $d p [1] [0] [0]$ 转移而来。

然后再考虑第 $1$ 段时间和第 $N$ 段时间之间睡觉的情况，计算最大恢复值之和。这时候需要注意第 $1$ 段时间被算作睡觉，因此需要从 $d p [1] [1] [1]$ 转移而来。同时最后转移时需要将第 $N$ 段时间算作睡觉，因此需要从 $d p [n] [b] [1]$ 进行转移。

最后将两种情况计算的最大值输出即可。

示例代码

#include<iostream>
#include<cstring>
using namespace std;
int n,b;
int val[3850];
int dp[3850][3850][2],ans;

int main(){
	cin>>n>>b;
	for(int i=1;i<=n;i++)cin>>val[i];
	
	memset(dp,-0x3f,sizeof dp);
	dp[1][1][1]=dp[1][0][0]=0;
	
	for(int i=2;i<=n;i++){
		dp[i][0][0]=dp[i-1][0][0];
		for(int j=1;j<=b;j++){
			dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]);
			dp[i][j][1]=max(dp[i-1][j-1][0],dp[i-1][j-1][1]+val[i]);
		}
	}
	ans=max(dp[n][b][0],dp[n][b][1]);
	
	memset(dp,-0x3f,sizeof dp);
	dp[1][1][1]=val[1];//第1个小时也记上了！
	dp[1][0][0]=0;
	
	for(int i=2;i<=n;i++){
		dp[i][0][0]=dp[i-1][0][0];
		for(int j=1;j<=b;j++){
			dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]);
			dp[i][j][1]=max(dp[i-1][j-1][0],dp[i-1][j-1][1]+val[i]);
		}
	}
	ans=max(ans,dp[n][b][1]);//第N个小时必须得摆！
	
	cout<<ans;
	
	return 0;
}