2023.7.23

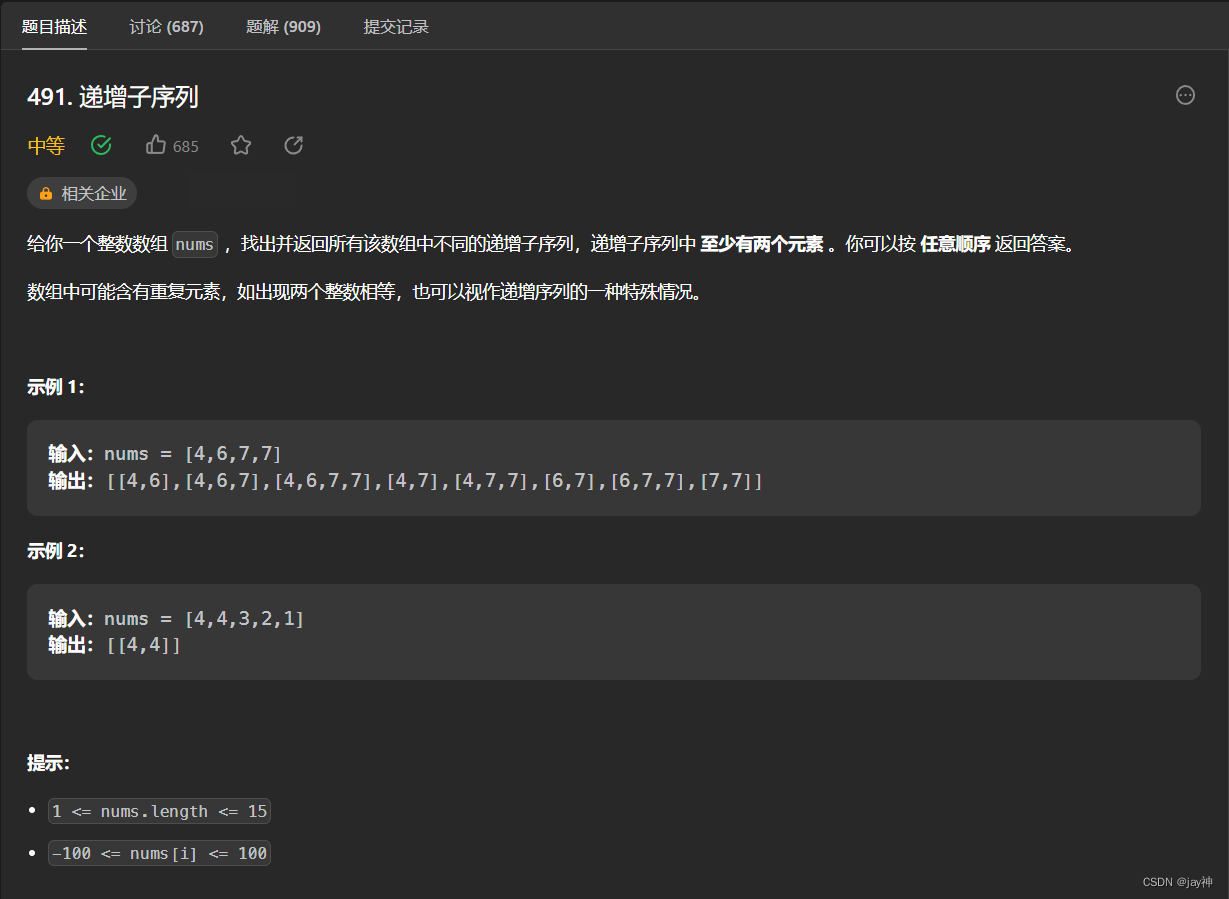
         本题本质上也是要选取递归树中的满足条件的所有节点，而不是选取叶子节点。 故在将符合条件的path数组放入ans数组后，不要执行return。 还一点就是这个数组不是有序的，并且也不能将它有序化，所以这里的去重操作不能和之前一样了，需要定义一个set容器存储每层元素的使用情况，即同一父节点下的同一层不能使用同一个元素。

        我定义了个判别path是否递增的函数，绕了弯子，下面看代码：

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    bool is_sort(vector<int> nums)
    {
        for(int i=0; i<nums.size(); i++)
        {
            if(i>0 && nums[i]<nums[i-1])
            {
                return false;
            }
        }
        return true;
    }
    void backtrating(vector<int> nums,int start)
    {
        if(path.size()>=2 && is_sort(path)) //此处不需要return，因为我们要加入的是树的所有节点而不是叶子节点。
        {
            ans.push_back(path);
        }
        //if(start >= nums.size()) return;
        unordered_set<int> used;
        for(int i=start; i<nums.size(); i++)
        {
            if(used.find(nums[i]) != used.end()) continue;//找到重复使用的元素 跳过本次循环
            used.insert(nums[i]);
            path.push_back(nums[i]);
            backtrating(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrating(nums,0);
        return ans;
    }
};

        下面看一下优化过后的，不需要定义判别递增的函数,在元素加入path前进行一次if判断：看加入之后是否符合递增：

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    // bool is_sort(vector<int> nums)
    // {
    //     for(int i=0; i<nums.size(); i++)
    //     {
    //         if(i>0 && nums[i]<nums[i-1])
    //         {
    //             return false;
    //         }
    //     }
    //     return true;
    // }
    void backtrating(vector<int> nums,int start)
    {
        if(path.size()>=2) //此处不需要return，因为我们要加入的是树的所有节点而不是叶子节点。
        {
            ans.push_back(path);
        }
        //if(start >= nums.size()) return;
        unordered_set<int> used;
        for(int i=start; i<nums.size(); i++)
        {
            if(used.find(nums[i]) != used.end()) continue;//找到重复使用的元素 跳过本次循环
            if(!path.empty() && nums[i]<path.back()) continue; //若为非递增 跳过本次循环
            used.insert(nums[i]);
            path.push_back(nums[i]);
            backtrating(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrating(nums,0);
        return ans;
    }
};

        上述代码可以进行优化，上面代码使用set来记录重复元素，由于题目中给出了nums中元素的大小范围：-100~100. 所以可以用一个大小为201的数组记录nums中所有元素的使用情况：

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    // bool is_sort(vector<int> nums)
    // {
    //     for(int i=0; i<nums.size(); i++)
    //     {
    //         if(i>0 && nums[i]<nums[i-1])
    //         {
    //             return false;
    //         }
    //     }
    //     return true;
    // }
    void backtrating(vector<int> nums,int start)
    {
        if(path.size()>=2) //此处不需要return，因为我们要加入的是树的所有节点而不是叶子节点。
        {
            ans.push_back(path);
        }
        //if(start >= nums.size()) return;
        //unordered_set<int> used;
        int used[201] ={0};
        for(int i=start; i<nums.size(); i++)
        {
            //if(used.find(nums[i]) != used.end()) continue;//找到重复使用的元素 跳过本次循环
            if(used[nums[i]+100] == 1) continue;
            if(!path.empty() && nums[i]<path.back()) continue; //若为非递增 跳过本次循环
            used[nums[i]+100] = 1;
            path.push_back(nums[i]);
            backtrating(nums,i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrating(nums,0);
        return ans;
    }
};