1.简述

      

第一部分：问题分析

（1）实验题目：拉格朗日插值算法

具体实验要求：要求学生运用拉格朗日插值算法通过给定的平面上的n个数据点，计算拉格朗日多项式Pn(x)的值，并将其作为实际函数f(x)的估计值。用matlab编写拉格朗日插值算法的代码，要求代码实现用户输入了数据点(xi,f(xi))、插值点之后，程序能够输出插值点对应的函数估值。

（2）实验目的：让同学们进一步掌握拉格朗日插值算法的原理以及运算过程，并且通过matlab编程培养实际的上机操作能力和代码能力。

第二部分：数学原理 

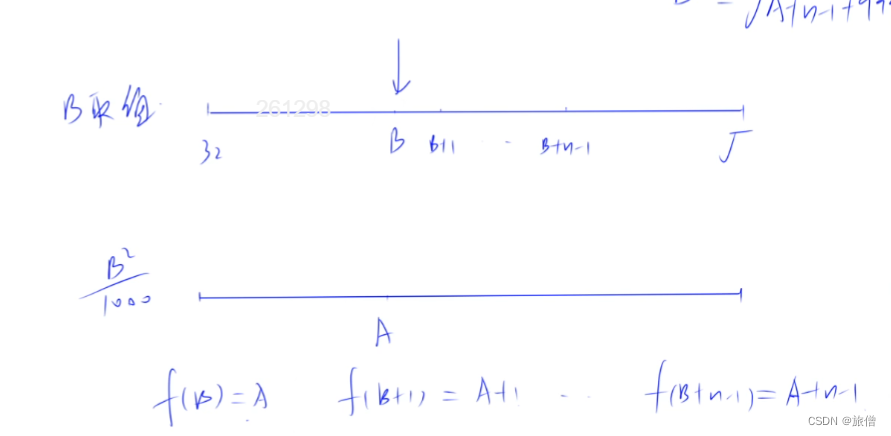
 要估计任一点ξ，ξ≠xi,i=0,1,2,...,n,则可以用Pn（ξ）的值作为准确值f(ξ)的近似值，此方法叫做“插值法”。

称式（*）为插值条件（准则），含xi(i=0,1,...,n)的最小区间[a,b]，其中a=min{x0,x1,...,xn}，b=max{x0,x1,...,xn}。
 

根据《插值多项式的性质》中的定理6.1可得

其中（6.19）称为基函数，（6.18）称为拉格朗日多项式，用（6.18）计算插值称为拉格朗日多项式插值。

2.代码

function Lagrange_main()
clc
x=0:1:10;
y=x./(cos(x)+1);
k=1;
for x0=0:0.1:10;
    y0(k)=Lagrange(x,y,x0);
    k=k+1;
end
x0=0:0.1:10;
plot(x0,y0)
hold on 
scatter(x,y,'ro')

end

function y0=Lagrange(x,y,x0)
n=length(x);
l=ones(1,n);
for k=1:n
    for j=1:n
        if j~=k
            l(k)=l(k)*(x0-x(j))/(x(k)-x(j));
        end
    end
end
y0=sum(y.*l);
end
 

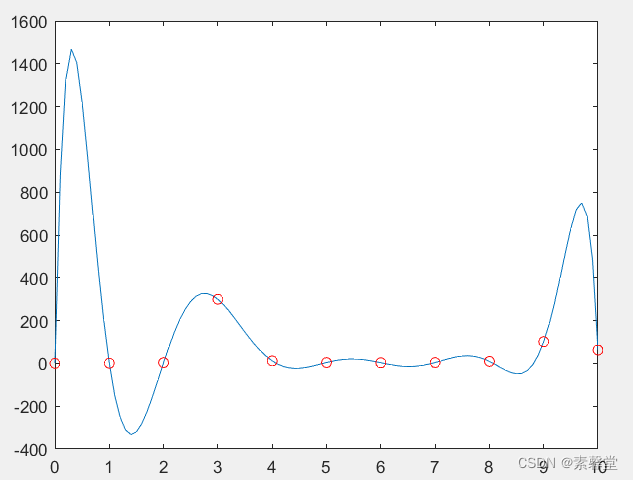
3.运行结果