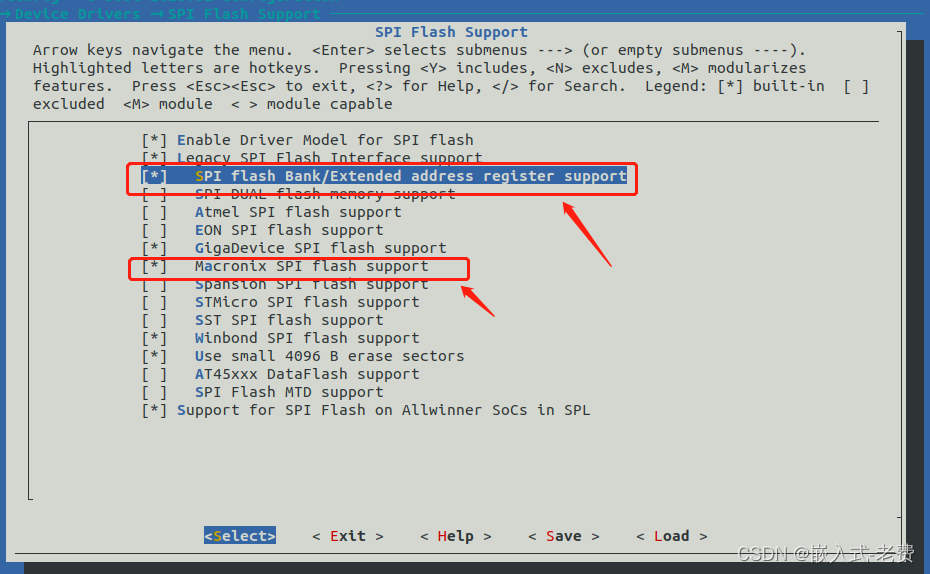
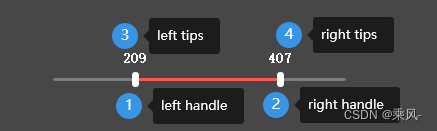
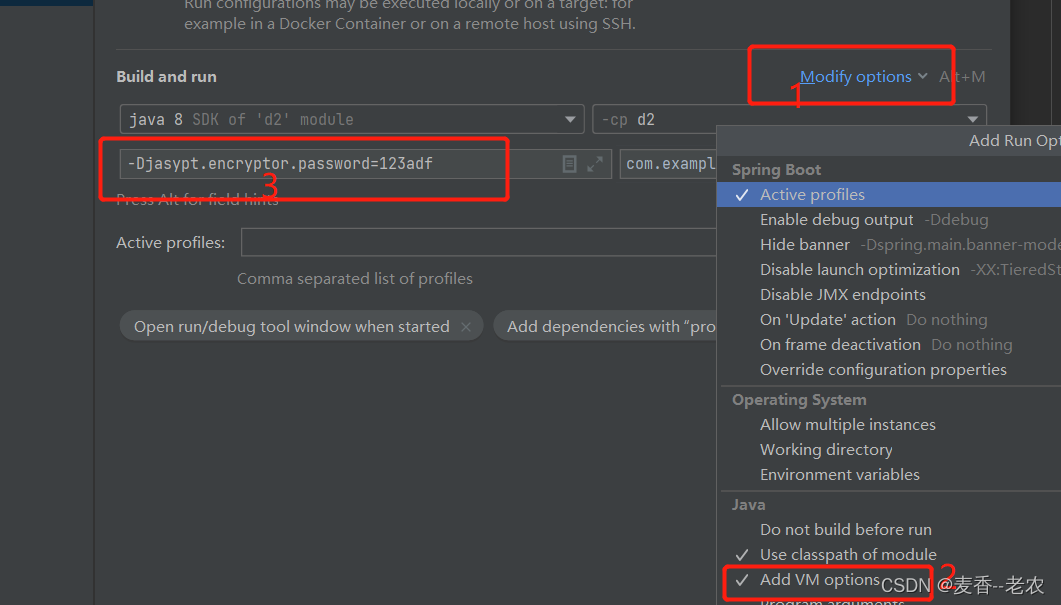
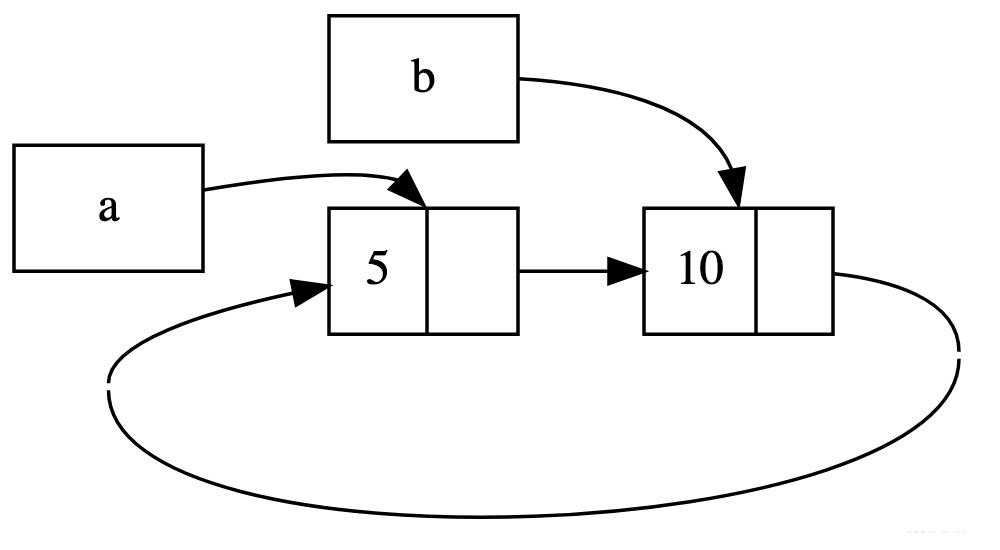
斜率优化DP
- AcWing 300. 任务安排1
- AcWing 301. 任务安排2
- AcWing 302. 任务安排3
- AcWing 303. 运输小猫
AcWing 300. 任务安排1
#include <iostream>
#include <cstring>
typedef long long LL;
using namespace std;
const int N = 5e3 + 10;
int st[N], sc[N];
LL f[N];//值考虑前i个任务,当前第i个任务是当前批次的最后一个任务,但是因为我们为了优化计算的时候加后面的费用,即费用提前计算,其实只有f[n]的状态是正确的
int n, S;
int main()
{
//input和前缀和
cin >> n >> S;
for (int i = 1; i <= n; ++ i)
{
cin >> st[i] >> sc[i];
st[i] += st[i - 1];
sc[i] += sc[i - 1];
}
//dp
memset(f, 0x3f, sizeof f); f[0] = 0;//别忘了初始化
for (int i = 1; i <= n; ++ i)//考虑当前i个任务
{
for (int j = 0; j < i; ++ j)//可以转移到i的合法状态
{
f[i] = min(f[i], f[j] + (LL)st[i] * (sc[i] - sc[j]) + (LL)S * (sc[n] - sc[j]));//S * (sc[n] - sc[j])费用提前计算
}
}
cout << f[n];
return 0;
}
后面这三题我懒得做了
AcWing 301. 任务安排2
AcWing 302. 任务安排3

斜率没有单调性了,本质上我们是想从我们维护的队列里面找一个斜率比当前要加进去的f[i]的斜率sumt[i] + S稍微大一点的数f[j],来进行状态转移,但是t可以取负数后,斜率sumt[i] + S不是随着i增加而单调递增的了,我们也不能在任务安排二中那样查找的时候删除一些可能用不到的状态了,每个状态都可能用到。
我们要在队列里面找一个斜率----这个斜率比我当前要加进去的f[i]的斜率sumt[i] + S稍大一些,这样我的f[j]的截距最小,也就是含+f[i]的式子值最小,即f[i]最小。
那我们如何找呢?
任务安排2可以借用sumt[i]+S的单调性,查询的时候好将斜率比我当前sumt[i]+S小的或等于的直接删掉,然后直接取队头f[q[hh]]进行状态转移。
任务安排3不能在查询的时候删去一些元素,因为sumt[i]+S不单调,从hh到tt的每个元素在后面的遍历中可能都有用。那从hh到tt那个元素经过斜率计算(用队列里的mid和mid+1两个点去计算)(因为f[q[]]不是斜率而是y)才是稍微比我当前的sumt[i]+S大呢,显然就是二分了,因为起码q[hh]到q[tt]存的f[]的下标值还是单调的,可以用二分
AcWing 303. 运输小猫