🏆今日学习目标：
🍀例题讲解P3375 【模板】KMP 字符串匹配
✅创作者：贤鱼
⏰预计时间：25分钟
🎉个人主页：贤鱼的个人主页
🔥专栏系列：c++
🍁贤鱼的个人社区，欢迎你的加入 贤鱼摆烂团

题目

【模板】KMP 字符串匹配

题目描述

给出两个字符串 $s_1$ 和 $s_2$，若 $s_1$ 的区间 $[l,r]$ 子串与 $s_2$ 完全相同，则称 $s_2$ 在 $s_1$ 中出现了，其出现位置为 $l$。
现在请你求出 $s_2$ 在 $s_1$ 中所有出现的位置。

定义一个字符串 $s$ 的 border 为 $s$ 的一个非 $s$ 本身的子串 $t$，满足 $t$ 既是 $s$ 的前缀，又是 $s$ 的后缀。
对于 $s_2$，你还需要求出对于其每个前缀 $s^{\prime }$ 的最长 border $t^{\prime }$ 的长度。

输入格式

第一行为一个字符串，即为 $s_1$。
第二行为一个字符串，即为 $s_2$。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 $s_2$ 在 $s_1$ 中出现的位置。
最后一行输出 $|s_2|$ 个整数，第 $i$ 个整数表示 $s_2$ 的长度为 $i$ 的前缀的最长 border 长度。

样例 #1

样例输入 #1

ABABABC
ABA

样例输出 #1

1
3
0 0 1

提示

样例 1 解释

。

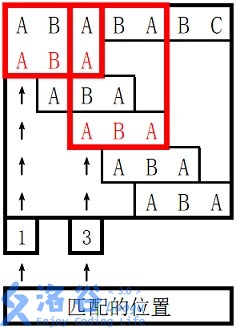对于 $s_2$ 长度为 $3$ 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 $1$。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

• Subtask 1（30 points）：$|s_1|\le 15$，$|s_2|\le 5$。
• Subtask 2（40 points）：$|s_1|\le 10^4$，$|s_2|\le 10^2$。
• Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 $1\le |s_1|,|s_2|\le 10^6$，$s_1,s_2$ 中均只含大写英文字母。

思路

这个题目主要分为两部分

1.判断s2在s1中出现的所有位置,从小到大输出

其实只需要从1-len1(s1长度)遍历就可以解决这个问题

2判断s2每一位的border长度

这个题n^3基础做法绝对会tle,题目也说了这是个kmp模板题
kmp如何理解?
假设答案为nxt[]
那么nxt[i]最大等一nxt[i-1]+1
多了一位字母border最多也就多一位
所以判断多的这一位字母和上一位+1的字母是否相同
相同了答案++,不同的话就去寻找再上一段的border
如果找到了0,就判断第一位和这一位是否相同,相同为1,不同为0
输出答案即可

AC代码

下面net就是nxt(打错了)

#include<cmath>
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char s1[10000005],s2[10000005];
int net[10000005];
int main(){
	cin>> (s1+1);
	cin>> (s2+1);
	int len1,len2;
	len1=strlen(s1+1);
	len2=strlen(s2+1);
	for(int i=1;i<=len1;i++){
		int f=0;
		int jj=i-1;
		for(int j=1;j<=len2;j++){
			jj++;
			//cout<<jj<<" "<<j<<" "<<s1[jj]<<s2[j]<<endl;
			if(s1[jj]!=s2[j]){
				f=1;
				break;
			}
		}
		if(!f)cout<<i<<endl;
	}
	net[1]=0;
	int j=0;
	for(int i=2;i<=len2;i++){
		while(j>0&&s2[i]!=s2[j+1]){
			j=net[j];
		}
		if(s2[i]==s2[j+1]) j++;
		net[i]=j;
	}
	for(int i=1;i<=len2;i++)
		cout<<net[i]<<" ";
}