分组密码算法是将输入数据划分成固定长度的组进行加密和解密的一类对称密码算法。本章主要介绍分组密码概述、DES、AES，以及分组密码的工作模式和分组密码分析。

1.分组密码简介

分组密码是一种单钥或对称密码算法，通信双方使用相同的密钥加密和解密。
在分组密码中，要将明文分为长度为n的分组，用同样的密钥k对每一个组进行加密，解密的时候同样的。设加密之后的密文长度为m，则如果m>n，则是有数据扩展的分组密码；如果m<n，则是有数据压缩的分组密码。

2.分组密码的基本原理

2.1代换

为使加密运算可逆也就是让解密运算可行，明文的每个分组都应该产生唯一一个密文分组，这样的变换是可逆的，称明文分组到密文分组的可逆变换称为代换。

2.2扩散

扩散和混淆的目的是抗击攻击者对密码系统的统计分析。
扩散是将明文的统计特性散步到密文中去，使明文的每位影响密文中的多位的值，等价于密文中每位都受到明文中多位的影响，也就是从密文中不能获得明文的统计特性。

2.3混淆

混淆是使密文和密钥之间的统计关系变得尽可能复杂，从而使得攻击者无法得到密钥。使用复杂的代数算法可以得到预期的混淆效果，而简单的线性代换函数得到的混淆结果不太理想。
扩散和混淆成功地实现了分组密码的本质属性，因而成为设计现代分组密码的基础。

3.分组密码的结构

现代密码学中的分组密码体制基本上都是基于乘积和迭代来构造的。乘积一般使通过一系列的置换和代换构成的。

3.1Feistel网络

分为平衡的和不平衡的两种。

3.1.1平衡Feistel网络

设x是需要加密的明文，长度为2m。
加密过程如下：
①将明文x一分为二，x=L₀R₀，L为左边m长度，R为右边m长度部分。
②

其中F是一个加密函数，称为圈函数；K_i是由密钥k产生的长度为t的子密钥；密文y=R_rL_r，其中r是圈变换的迭代次数。解密过程就是加密过程的逆过程。
过程图如下：

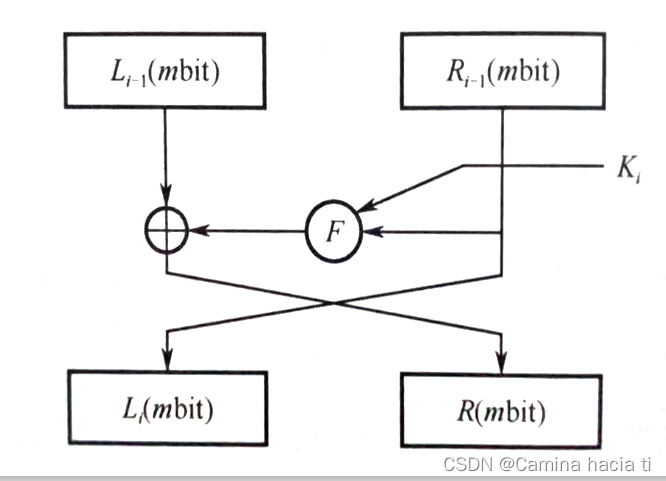
3.1.2不平衡Feistel网络

设x是需要加密的明文，长度为2m。
加密过程如下：
①将明文x一分为二，x=L₀R₀，L为左边n₁长度，R为右边n₂长度部分，且n₁+n₂=2m。
②
其中F是圈变换；K_i是由密钥k产生的长度为t的子密钥；密文y=X_r^RX_r^L，其中r是圈变换的迭代次数。解密过程与加密过程类似。

其中有限域的概念可以参考如下链接：有限域

3.2SP网络

SP型分组密码的加密思想为：设x是要加密的明文，长度为n。过程如下：
①令X₀=x，1 ≤ i ≤ r；
②在子密钥K_i的控制下，对X_i-1进行代换S；
③对结果做置换或者可逆的线性变换P得到结果X_i
④重复2、3步直到达到迭代次数r，得到最后的密文结果y=X_r。
过程如下图：

其中S一般称为混淆层，起混淆作用；
置换或者可逆的线性变换P称为扩散层，起扩散作用。

Fesistel网络的加解密过程类似，但是SP网络的加解密过程布雷斯，所以不能用同一个算法来实现加密和解密。

4.分组密码的设计

分组密码的设计在于找到一种算法，能在密钥控制下从一个足够大且足够好的置换子集中，简单而迅速地选出一个置换，用来对当前输入的明文组进行加密变换。
设计要求如下：
①分组长度n要足够大，使分组代换字母表中的元素个数2ⁿ足够大，防止明文穷举攻击奏效。
②密钥量要足够大，以防止密钥穷举攻击奏效。
③由密钥确定置换的算法要足够复杂。
④加密和解密运算简单，易于软件和硬件高速实现。
⑤数据扩展。一般无数据扩展，在采用同态置换和随机化加密技术时可以引入数据扩展。
⑥差错传播尽可能小。
其中1 2 3的安全性是必要条件。要在安全性和实用性之间找到平衡。