本篇博客会讲解力扣“94. 二叉树的中序遍历”的解题思路，这是题目链接。

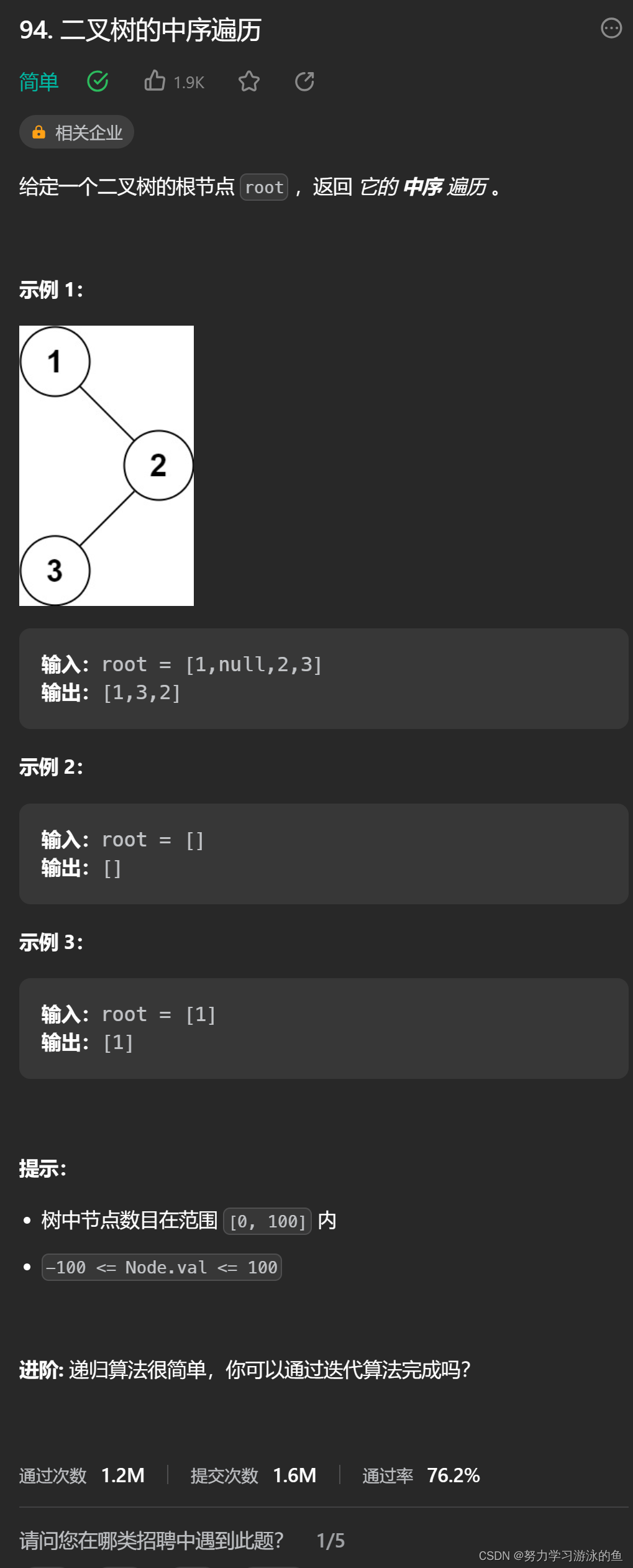
如何对二叉树进行中序遍历呢？所谓中序遍历，即先遍历左子树，接着遍历根节点，最后遍历右子树的一种遍历方式。具体来说，假设有某一种“操作”，我们称之为“中序遍历”，那么这个操作就是：先对左子树(root->left)做这个操作，接着访问根节点的数据，最后对右子树(root->right)做这个操作。

当然，题目要求返回一个数组，存储中序遍历访问到的数据，我们需要提前知道数组需要开辟多大的空间，这就可以通过一个函数TreeSize来实现。TreeSize函数负责求二叉树结点的个数，方法是：如果是一棵空树(root == NULL)，那么结点数是0，否则结点数是左子树(root->left)的结点数与右子树(root->right)的结点数之和。

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : 
        TreeSize(root->left) + TreeSize(root->right) + 1;
}

void _inorderTraversal(struct TreeNode* root, int* a, int* pi)
{
    if (root == NULL)
    {
        return;
    }

    // 左子树 根 右子树
    _inorderTraversal(root->left, a, pi);
    a[(*pi)++] = root->val;
    _inorderTraversal(root->right, a, pi);
}

int* inorderTraversal(struct TreeNode* root, int* returnSize){
    // 求二叉树结点个数，开辟空间
    *returnSize = TreeSize(root);
    int* ret = (int*)malloc(sizeof(int) * *returnSize);

    int i = 0;
    _inorderTraversal(root, ret, &i);

    return ret;
}

总结

大家需要牢牢掌握中序遍历的特点：中序遍历是一种“操作”，这种操作具体来说是：先对左子树(root->left)做这种操作，再访问根节点的数据，最后对右子树(root->right)做这种操作。

感谢大家的阅读！