论文笔记--ERNIE: Enhanced Language Representation with Informative Entities
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 模型框架
- 3.2 K-Encoder(Knowledgeable Encoder)
- 3.3 预训练任务
- 3.4 微调
- 4. 文章亮点
- 5. 原文传送门
- 6. References
1. 文章简介
- 标题:ERNIE: Enhanced Language Representation with Informative Entities
- 作者:Zhengyan Zhang, Xu Han, Zhiyuan Liu, Xin Jiang, Maosong Sun, Qun Liu
- 日期:2019
- 期刊:ACL
2. 文章概括
文章提出了ERNIE(Enhanced Language Representation with Informative Entities),一种可以将外部知识融合进入预训练模型的方法。数值实验表明,ERNIE可以提升一些知识驱动的下游任务的表现,且在其它NLP任务上效果基本持平SOTA。
3 文章重点技术
3.1 模型框架
给定token序列
{
w
1
,
…
,
w
n
}
\{w_1, \dots, w_n\}
{w1,…,wn},其中
n
n
n为序列长度,令
{
e
1
,
…
,
e
m
}
\{e_1, \dots, e_m\}
{e1,…,em}表示对应的实体序列,其中
m
m
m为实体数。一般来说
m
<
n
m<n
m<n,这是因为不是每个token都可以映射为知识图谱(KG)中的实体(entity),且一个实体可能对应多个token,比如"bob dylan"两个token对应一个实体"Bob Dylan"。记所有token的词表为
V
\mathcal{V}
V,KG中所有实体的集合为
E
\mathcal{E}
E。如果对
v
∈
V
v\in\mathcal{V}
v∈V,存在与其对应的实体
e
∈
E
e\in\mathcal{E}
e∈E,则我们用
f
(
v
)
=
e
f(v)=e
f(v)=e表示这种对齐关系。特别地,针对上述多个token对应单个实体的情况,我们将实体对齐给第一个token,例如句子中出现"bob dylan…"时,
f
(
"bob"
)
=
"Bob Dylan"
f(\text{"bob"}) = \text{"Bob Dylan"}
f("bob")="Bob Dylan"。
如下图所示,ERNIE的整体框架分为两部分:1) T-Encoder(Textual encoder),用于捕捉基本的词义和句法信息;2) K-Encoder(Knowledgeable encoder),用于将外部知识融合进入模型。记T-Encoder的层数为
N
N
N,K-Encoder的层数为
M
M
M。
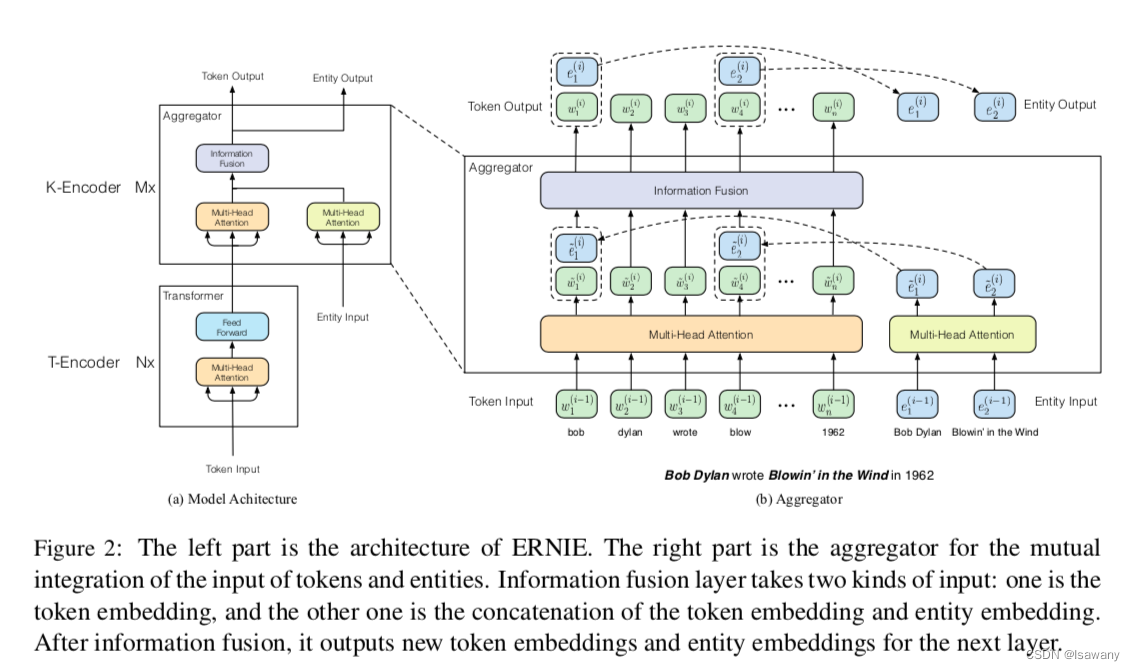
具体来说,给定输入序列
{
w
1
,
…
,
w
n
}
\{w_1, \dots, w_n\}
{w1,…,wn}和对应的实体序列
{
e
1
,
…
,
e
m
}
\{e_1, \dots, e_m\}
{e1,…,em},T-encoder层首先将token序列、segment序列和位置序列输入得到词汇和句法层面的特征
{
w
1
,
…
,
w
n
}
=
T-Encoder
(
{
w
1
,
…
,
w
n
}
)
\{\bold{w}_1, \dots, \bold{w}_n\} = \text{T-Encoder}(\{w_1, \dots, w_n\})
{w1,…,wn}=T-Encoder({w1,…,wn}),其中T-Encoder结构和BERT[1]相同,基本架构为Transformer的Encoder层。
然后将上述特征传入到K-Encoder层。K-Encoder还会接受外部知识信息,首先我们会通过TransE生成
{
e
1
,
…
,
e
m
}
\{e_1, \dots, e_m\}
{e1,…,em}对应的预训练实体嵌入
{
e
1
,
…
,
e
m
}
\{\bold{e}_1, \dots, \bold{e}_m\}
{e1,…,em},然后将该嵌入同上述特征
{
w
1
,
…
,
w
n
}
\{\bold{w}_1, \dots, \bold{w}_n\}
{w1,…,wn}一起输入K-Encoder层从而得到融合外部知识的输出嵌入:
{
w
1
o
,
…
,
w
n
o
}
,
{
e
1
o
,
…
,
e
m
o
}
=
K-Encoder
(
{
w
1
,
…
,
w
n
}
,
{
e
1
,
…
,
e
m
}
)
\{\bold{w}_1^o, \dots, \bold{w}_n^o\},\{\bold{e}_1^o, \dots, \bold{e}_m^o\} = \text{K-Encoder}(\{\bold{w}_1, \dots, \bold{w}_n\},\{\bold{e}_1, \dots, \bold{e}_m\})
{w1o,…,wno},{e1o,…,emo}=K-Encoder({w1,…,wn},{e1,…,em}),上述输出嵌入后续可用来作为特征参与下游任务。
3.2 K-Encoder(Knowledgeable Encoder)
如上图所示,K-Encoder包含堆叠的聚合器,每个聚合器包含token和实体两部分输入。在第 i i i个聚合器中,输入为来自上层聚合器的嵌入 { w 1 ( i − 1 ) , … , w n ( i − 1 ) } \{\bold{w}_1^{(i-1)}, \dots, \bold{w}_n^{(i-1)}\} {w1(i−1),…,wn(i−1)}和实体嵌入 { e 1 ( i − 1 ) , … , e m ( i − 1 ) } \{\bold{e}_1^{(i-1)}, \dots, \bold{e}_m^{(i-1)}\} {e1(i−1),…,em(i−1)},然后将token和实体嵌入分别传入到两个多头自注意力机制MH-ATTs得到各自的输出: { { w ~ 1 ( i ) , … , w ~ n ( i ) } = MH-ATT ( { w 1 ( i − 1 ) , … , w n ( i − 1 ) } ) { e ~ 1 ( i ) , … , e ~ m ( i ) } = MH-ATT ( { e 1 ( i − 1 ) , … , e m ( i − 1 ) } ) \begin{cases}\{\bold{\tilde{w}}_1^{(i)}, \dots, \bold{\tilde{w}}_n^{(i)}\} = \text{MH-ATT}(\{\bold{w}_1^{(i-1)}, \dots, \bold{w}_n^{(i-1)}\})\\ \{\bold{\tilde{e}}_1^{(i)}, \dots, \bold{\tilde{e}}_m^{(i)}\} = \text{MH-ATT}(\{\bold{e}_1^{(i-1)}, \dots, \bold{e}_m^{(i-1)}\})\end{cases} {{w~1(i),…,w~n(i)}=MH-ATT({w1(i−1),…,wn(i−1)}){e~1(i),…,e~m(i)}=MH-ATT({e1(i−1),…,em(i−1)})。然后模型通过将每个token与其对应的实体进行拼接,将外部实体信息融合进入嵌入。具体来说,针对一个有与之对应的实体的token,假设 e k = f ( w j ) e_k=f(w_j) ek=f(wj),则 h j = σ ( W ~ t ( i ) w ~ j ( i ) + W ~ e ( i ) e ~ k ( i ) + b ~ ( i ) ) \bold{h}_j = \sigma(\bold{\tilde{W}}_t^{(i)} \bold{\tilde{w}}_j^{(i)} + \bold{\tilde{W}}_e^{(i)} \bold{\tilde{e}}_k^{(i)} + \bold{\tilde{b}}^{(i)}) hj=σ(W~t(i)w~j(i)+W~e(i)e~k(i)+b~(i))为整合了实体和token信息的隐藏层输出, w j ( i ) = σ ( W t ( i ) h j + b ~ t ( i ) ) e k ( i ) = σ ( W e ( i ) h j + b ~ e ( i ) ) \bold{w}_j^{(i)} = \sigma (\bold{W}_t^{(i)} \bold{h}_j + \bold{\tilde{b}}_t^{(i)})\\\bold{e}_k^{(i)} = \sigma (\bold{W}_e^{(i)} \bold{h}_j + \bold{\tilde{b}}_e^{(i)}) wj(i)=σ(Wt(i)hj+b~t(i))ek(i)=σ(We(i)hj+b~e(i))表示当前聚合器的输出嵌入,其中 σ \sigma σ为GELU激活函数。对于没有与之对应实体的token,只需要把上述涉及 e e e的部分拿掉即可: h j = σ ( W ~ t ( i ) w ~ j ( i ) + b ~ ( i ) ) w j ( i ) = σ ( W t ( i ) h j + b ~ t ( i ) ) \bold{h}_j = \sigma(\bold{\tilde{W}}_t^{(i)} \bold{\tilde{w}}_j^{(i)} + \bold{\tilde{b}}^{(i)})\\\bold{w}_j^{(i)} = \sigma (\bold{W}_t^{(i)} \bold{h}_j + \bold{\tilde{b}}_t^{(i)}) hj=σ(W~t(i)w~j(i)+b~(i))wj(i)=σ(Wt(i)hj+b~t(i))
3.3 预训练任务
为了将知识融合进入语言表达,文章提出了一种新的预训练任务:dEA(denoising entity auto-encoder):随机掩码一些token-entity的对齐,然后让模型给予对齐的tokens来预测被掩码的实体。具体来说,给定输入序列
{
w
1
,
…
,
w
n
}
\{w_1, \dots, w_n\}
{w1,…,wn}和对应的实体序列
{
e
1
,
…
,
e
m
}
\{e_1, \dots, e_m\}
{e1,…,em},通过下述公示预测token
w
i
w_i
wi对应的实体分布:
p
(
e
j
∣
w
i
)
=
exp
(
linear
(
w
i
o
)
⋅
e
j
)
∑
k
=
1
m
exp
(
linear
(
w
i
o
)
⋅
e
k
)
p(e_j|w_i) = \frac {\exp (\text{linear}(\bold{w}_i^o) \cdot \bold{e}_j)}{\sum_{k=1}^m \exp (\text{linear}(\bold{w}_i^o) \cdot \bold{e}_k)}
p(ej∣wi)=∑k=1mexp(linear(wio)⋅ek)exp(linear(wio)⋅ej)。
考虑到实际对齐过程中可能存在一些错误,我们增加如下策略:1)5%的时间用随机的实体替代当前实体,使得模型纠正token-实体对齐错误的情况 2)15%的时间将token-实体对齐进行掩码,使得模型可以纠正当实体对齐为被识别到的情况 3)其余时间保持token-实体对齐不变,从而使得模型学习到token和实体之间的对齐方法。
最终,ERNIE使用MLM、NSP和上述dEA三种训练目标。
3.4 微调
类似于BERT,我们使用[CLS]的嵌入作为句子的最终嵌入表示来进行分类。针对关系分类任务,我们增加[HD]和[TL]表示head/tail实体的开头和结尾;针对实体抽取任务,我们增加[ENT]表示实体位置。
4. 文章亮点
文章提出了一种可以将外部信息融合至预训练的ERNIE模型。实验表明,ERNIE可以有效地将KG中的信息注入到预训练模型,从而使得模型在处理实体提取、关系分类等需要外部知识的任务时更加出色,且实验证明外部知识可以帮助模型充分利用少量的训练集。
5. 原文传送门
ERNIE: Enhanced Language Representation with Informative Entities
6. References
[1] 论文笔记–BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
[2] 百度ERNIE论文笔记–ERNIE: Enhanced Representation through Knowledge Integration