概念
红黑树(Red-Black Tree)是一种自平衡的二叉搜索树,它在插入和删除节点时通过一系列的旋转和重新着色操作来保持树的平衡。红黑树的平衡性质使得它在插入、删除和查找等操作上具有较好的性能。
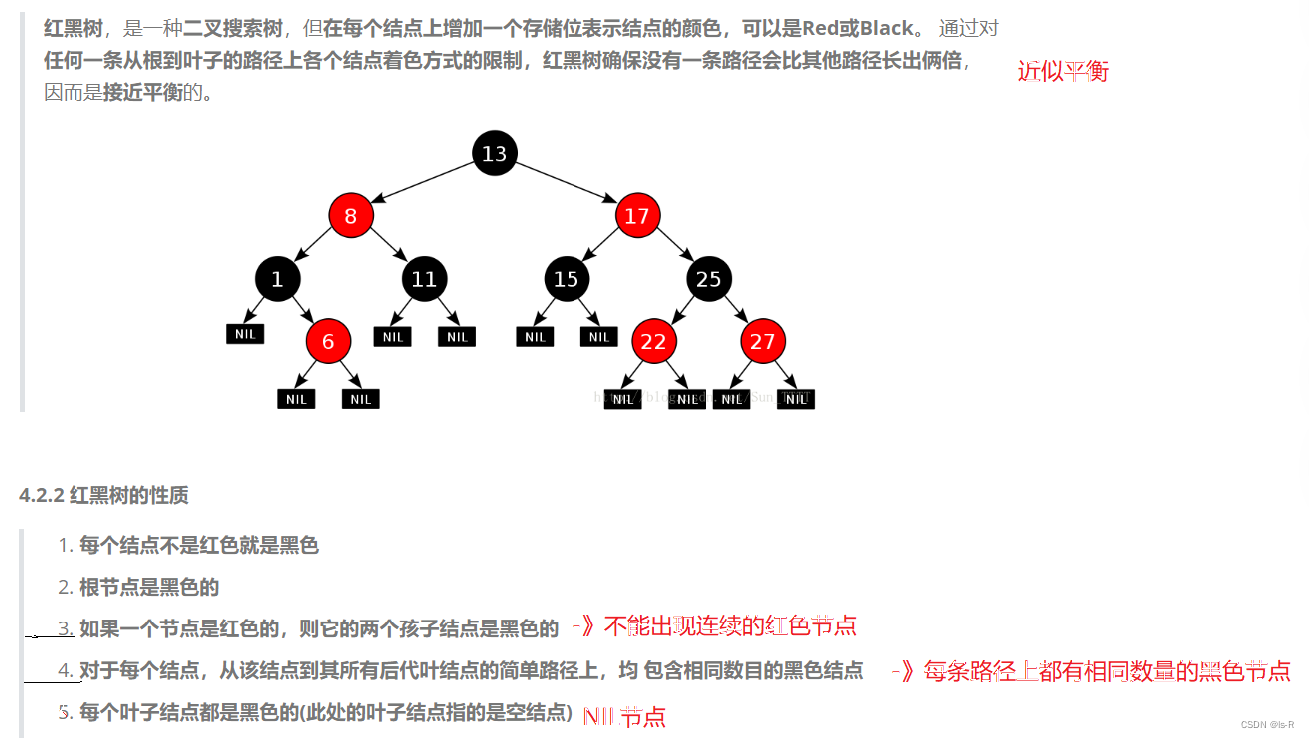
红黑树具有以下特点:
- 每个节点都有一个颜色,要么是红色,要么是黑色。
- 根节点是黑色的。
- 所有叶子节点(NIL节点)都是黑色的。
- 如果一个节点是红色的,则它的两个子节点都是黑色的。
- 对于每个节点,从该节点到其所有后代叶子节点的简单路径上,均包含相同数量的黑色节点。
红黑树相比于AVL树有以下优势:
- 红黑树的平衡性相对AVL树更加宽松,因此插入和删除操作可能需要更少的旋转操作。这使得红黑树在某些场景下的性能更好,特别是在需要频繁插入和删除节点的情况下。
- 红黑树的平衡操作相对AVL树更加简单,只需要进行旋转和重新着色操作,而不需要像AVL树那样进行更复杂的平衡调整。
- 红黑树的平衡因子只有两种可能的取值(0和1),而AVL树的平衡因子可能有三种取值(-1、0和1)。这意味着红黑树可以使用一个比AVL树更小的字段来存储节点的平衡信息。
总的来说,红黑树在平衡性和性能之间取得了一种平衡,适用于需要高效的插入和删除操作的场景。AVL树则更适用于对插入和删除操作的次数没有特别严格要求,但对查找操作有严格性能要求的场景。选择使用红黑树还是AVL树取决于具体的应用需求和对性能的权衡考虑。

若插入一个新节点,要插入红色(可违反规则3,不违反规则4)
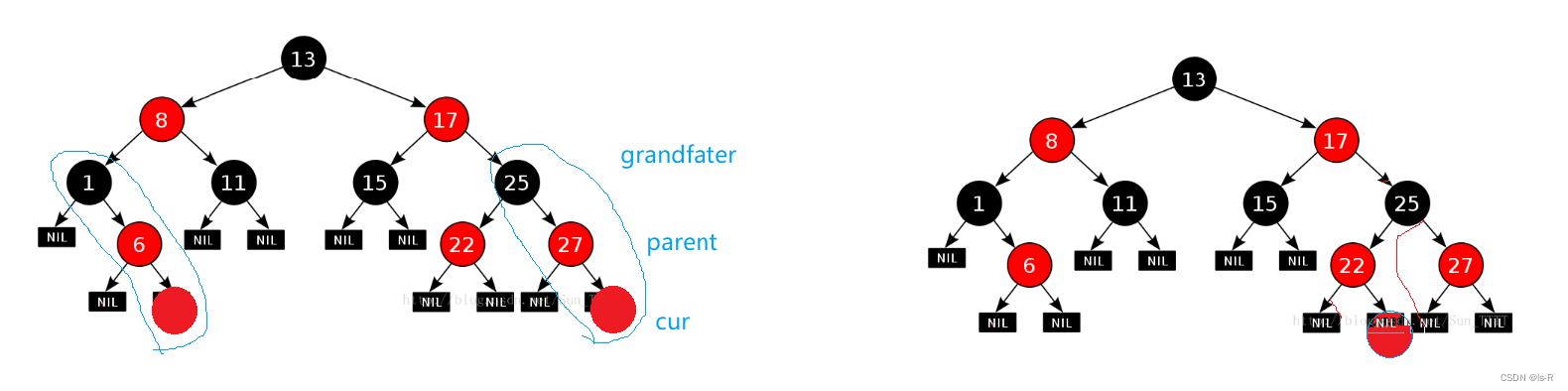
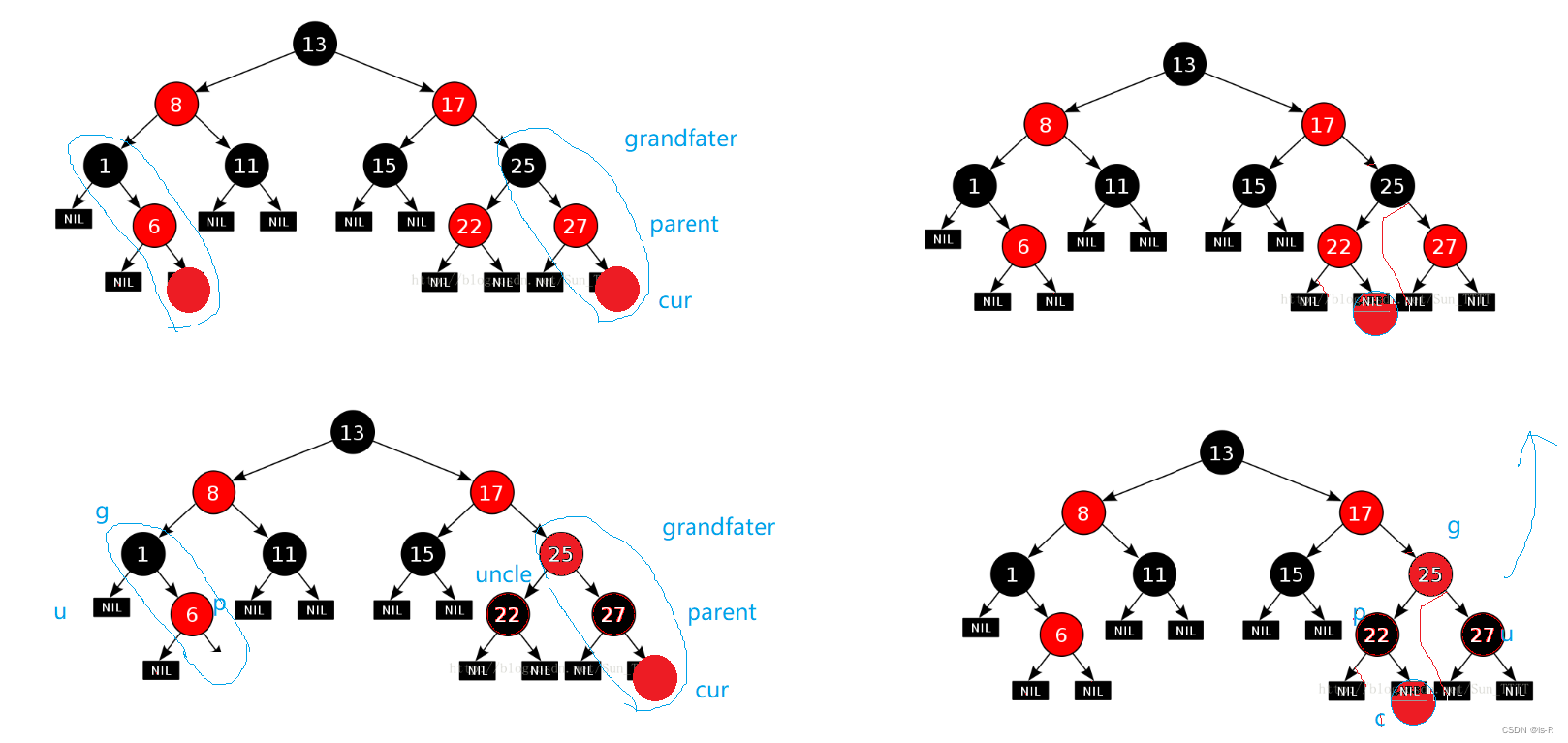
在红黑树中,当插入一个节点时,需要通过一系列的旋转和重新着色操作来保持树的平衡。下面是红黑树插入节点时的变色规则:
- 如果插入的节点是根节点,将其着色为黑色。
- 如果插入的节点的父节点是黑色,不需要进行任何操作,树仍然是平衡的。
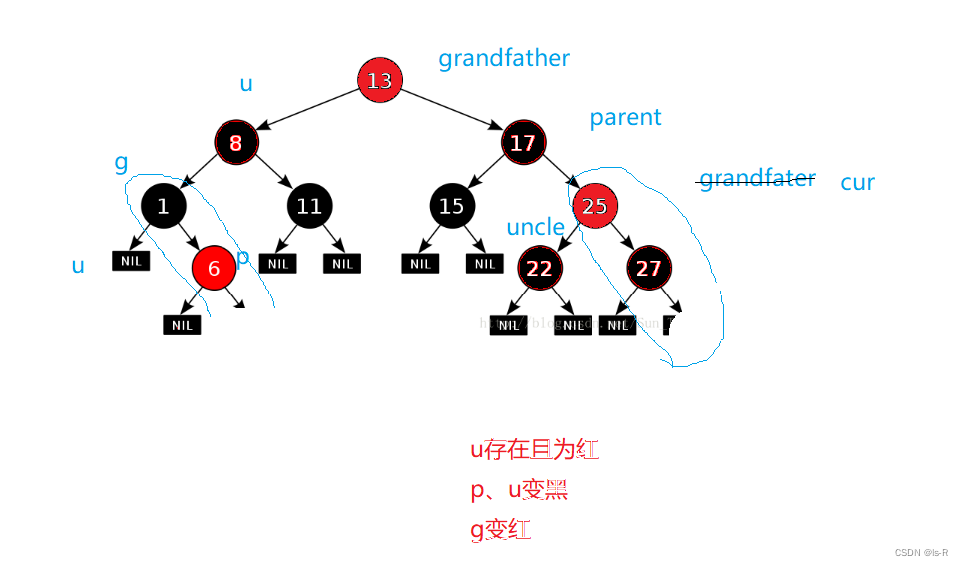
- 如果插入的节点的父节点是红色:
- 如果插入的节点的叔叔节点是红色,将父节点和叔叔节点着色为黑色,将祖父节点着色为红色,然后将当前节点指向祖父节点,继续进行后续操作。
- 如果插入的节点的叔叔节点是黑色或者NIL节点:
- 如果插入节点是父节点的左子节点,且父节点是祖父节点的左子节点,进行右旋操作。
- 如果插入节点是父节点的右子节点,且父节点是祖父节点的右子节点,进行左旋操作。
- 如果插入节点是父节点的左子节点,且父节点是祖父节点的右子节点,进行左旋操作,然后将当前节点指向新的父节点,继续进行后续操作。
- 如果插入节点是父节点的右子节点,且父节点是祖父节点的左子节点,进行右旋操作,然后将当前节点指向新的父节点,继续进行后续操作。
- 重复步骤3,直到当前节点变为根节点或者满足红黑树的所有性质。
通过上述变色规则,红黑树保持了平衡性质,并且确保了树的黑色节点数量相等,从而保证了红黑树的平衡性。