题目描述

You are given a graph with n vertices and m undirected edges of length 1. You can do the following operation on the graph for arbitrary times:

Choose an edge (u,v) and replace it by two edges, (u,w) and (w,v), where w is a newly inserted vertex. Both of the two edges are of length 1.

You need to find out the maximum number of vertices whose minimum distance to vertex 1 is no more than k.

输入描述:

The first line contains three integers n (1≤n≤10^5), m (0≤m≤2⋅10^5)and k (0≤k≤10^9).
Each of the next m lines contains two integers u and v (1≤u,v≤n), indicating an edge between u and v. It is guaranteed that there are no self-loops or multiple edges.

输出描述:
Output an integer indicating the maximum number of vertices whose minimum distance to vertex 1 is no more than k.

输入：

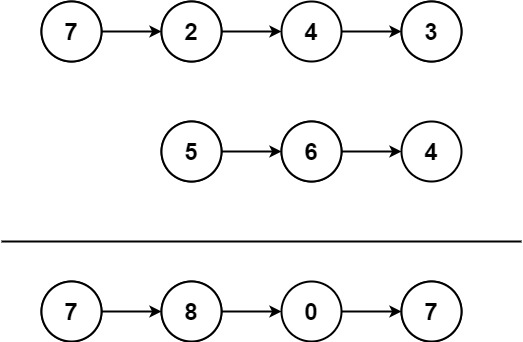
8 9 3
1 2
1 3
1 5
3 4
3 6
4 5
5 6
6 7
7 8

输出：

15

题意：给定n个点，m条边，k为给定数值，你有一种操作，相当于你选择一条边，加入任意个点，可以操作任意次，问最后从1出发能到达的点的总数最大。

解析：求一次bfs树，把非树边的边进行拓展 ，也同时把叶子节点进行拓展，此时就是最优的情况，至于证明，引用下官方题解专业证明.

注意：特判一下没有边的情况，遍历叶子节点时候直接从2开始，因为1为根节点，不能算叶子节点。

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
typedef pair<int,ll> PII;
vector<int> v[N];
int in[N];//记录入度,入度为1即是叶子节点
map<PII,int> mp;
struct node
{
    int a,b;
    bool flag;//是否为非树边
}tr[N];
ll dist[N];//记录从1出发到点u的距离
void bfs()
{
    queue<int> q;
    q.push(1);
    memset(dist,-1,sizeof dist);
    dist[1]=0;
    while(q.size())
    {
        int u=q.front();
        q.pop();
        for(int i=0;i<v[u].size();i++)
        {
            int j=v[u][i];
            if(dist[j]==-1)
            {
                dist[j]=dist[u]+1;
                q.push(j);
                tr[mp[{u,j}]].flag=true;//为树边
                tr[mp[{j,u}]].flag=true;//为树边
            }
        }
    }
}
void solve()
{
    int n,m,k;
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        tr[i]={a,b};
        mp[{a,b}]=i;
        v[a].push_back(b);
        v[b].push_back(a);
        in[a]++,in[b]++;
    }
    if(m==0)
    {
        printf("1\n");
        return;
    }
    bfs();
    ll ans=1;//自身
    for(int i=1;i<=m;i++)
    {
        int a=tr[i].a,b=tr[i].b;
        bool flag=tr[i].flag;
        if(!flag)//是非树边,进行拓展
        {
            //注意需要判断dist是否为-1,-1表示无法到达
            if(dist[a]<k&&dist[a]!=-1) ans+=k-dist[a];
            if(dist[b]<k&&dist[b]!=-1) ans+=k-dist[b];
            tr[mp[{a,b}]].flag=true;//此时表示已经使用过
            tr[mp[{b,a}]].flag=true;
        }
    }
    for(int i=2;i<=n;i++)
    {
        if(dist[i]!=-1&&in[i]==1&&dist[i]<k) ans+=k-dist[i];
        if(dist[i]!=-1&&dist[i]<=k) ans++;
    }
    printf("%lld\n",ans);
}
int main()
{
    int t=1;
    //scanf("%d",&t);
    while(t--) solve();
    return 0;
}