目录
1 目标问题: 什么是条件期望? 条件期望有什么用?
2 条件期望,全期望公式
3 条件期望,全期望公式 和 条件概率,全概率公式的区别和联系
3.1 公式如下
3.2 区别和联系
3.3 概率和随机过程
4 有什么用:---可以解决很多递归的问题
4.1 使用前有个前提:界定清楚你要求的随机变量的目标和类型
4.1.1 求的是次数,还是数量?
4.1.2 确定你要求的目标变量
4.2 例题1:计算出去的 时间= 步数 =次数,属于这一类问题
4.3 例题3:求次数,计算几何分布的期望
4.4 例题3:求个数
5 条件期望,全期望公式和 马尔可夫转移
1 目标问题: 什么是条件期望? 条件期望有什么用?
这次先不说目标,先引用一个小学数学题作为开头
Q:假设已知1班平均分是93,2班平均分是95,那么两个班的平均分怎么算?
错误算法: (93+95)/2=94
- 除非两个班的学生数量一样,否则就是错的
- 这个不能用简单算术平均,得用加权平均
正确算法
- 假设1班学生数量n1,平均分A1=93,假设2班学生数量n2,平均分A2=95
- 根据平均分的定义
- A0 = 总分数/总人数
- = (A1*n1 + A2*n2)/(n1+n2)
- = n1/(n1+n2)*A1 + n2/(n1+n2)*A2
- = 系数1*A1+系数2*A2
- = 人数权重比例1*A1+人数权重比例2*A2
- 而权重 = 本班人数/ sum(所有班级人数和)
从这里引出了一个问题
Q1: 我们想知道总体的平均值,当然可以直接用总体的数计算,比如A0 = 总分数/总人数。但是如果我们已经知道了 总体的每个部分的平均值,是否可以根据这些算出总体的平均值呢?
A1: 答案是可以的,前面这个例子已经看到是可以的,总体均值= Σ部分均值*权重比例。
Q2: 接着问,如果这个总体不是确定的,而是一个随机变量,比如我们要求的是:这个随机变量的期望呢?
A2: 那么权重比例就变成了随机变量的概率,其实这个也就是 条件期望和全期望公式的内容
因此,引出了我们要讨论的主题:
- 类比: 总体均值= Σ部分均值*权重比例
- 全期望可以这么看
- E(X) = ΣPi*E(X|Yi) 和上面是同一个表达方式
- E(X) =E(E(X|Y))
- E(X) = P1*E(X|Y1) + ..... +Pk*E(X|Yk) = ΣPi*E(X|Yi)
- E(X) = E(E(X|Y)) = ΣPI*E(X|Yi) = P1*E(X|Y1) + ..... +Pk*E(X|Yk) ,其中i属于(1,k)
2 条件期望,全期望公式
下面不同写法的概念是不同的
step1: E(X) 是一个具体的数,随机变量的数学期望=随机变量的(概率)加权平均值=具体的数
step2: 因为在Y=y1的前提下,X还是有可能有几种情况,假设也是x1,x2...xk
所以条件期望 E(X|Y=y1) = Σxi*P(xi|Y=y1) = x1*P(x1|Y=y1) +x2*P(x2|Y=y1) +...+xk*P(xk|Y=y1)
step3: 而对于随机变量X,Y还有多个取值y1,y2....yj,比如 E(X|Y=y1) 本身还对应着一个概率 Pj
因此可以求期望 E(E(X|Y)) =ΣPI*E(X|Yj) = P1*E(X|Y1) + P2*E(X|Y2) +..... +Pj*E(X|Yj)
而实际上可证明,E(E(X|Y))=E(X)
step4: 所以全期望公式
E(X) = E(E(X|Y)) = ΣPI*E(X|Yi) = P1*E(X|Y1) + P2*E(X|Y2) + ..... +Pj*E(X|Yj) ,其中i属于(1,j)
看下面的图理解
图是知乎的,参考 zhuanlan.zhihu.com/p/612709393
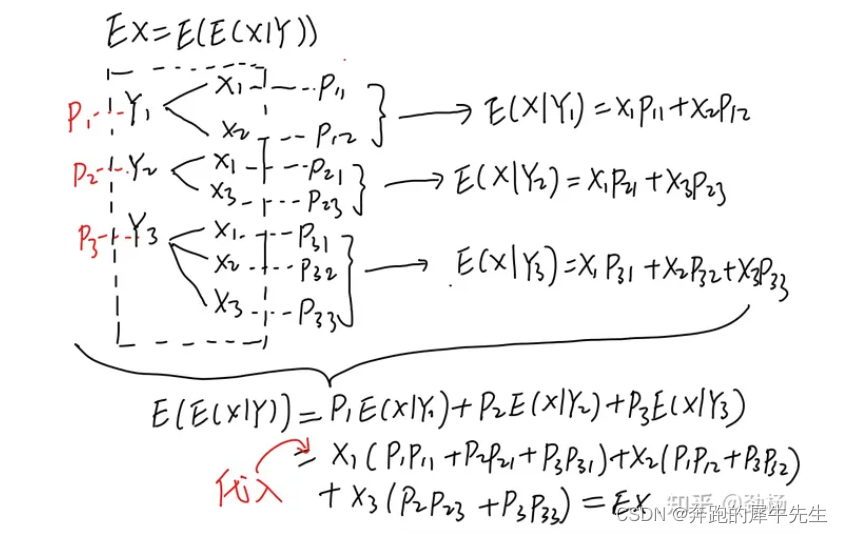
3 条件期望,全期望公式 和 条件概率,全概率公式的区别和联系
3.1 公式如下
- 条件概率: P(A|B) = P(AB) / P(B)
- 全概率公式: P(A) = P(AB1) * P(B1) +P(AB2) * P(B2) + ......+P(ABn) * P(Bn)
- 条件期望: E(X|Y=y1) =E(X|y1) = Σxi*P(xi|Y=y1)
- 全期望公式: E(X) = E(E(X|Y)) = ΣPj*E(X|Yj) = P1*E(X|Y1) + ..... +Pj*E(X|Yj) ,其中j属于(1,k)
3.2 区别和联系
- 条件概率,全概率公式,是用来求概率的
- 条件期望,全期望公式,是用来求各种 随机变量的期望值,而不是概率,比如,合成的平均次数,合成的目标的平均数量... ... 等等。
3.3 概率和随机过程
- 概率一般是求 瞬时/切面的发生可能,主要关注概率
- 随机过程,一般是求一个时间过程内的情况,或一个时间过程后的情况,可以关注概率,次数,数量。。。等等
4 有什么用:---可以解决很多递归的问题
4.1 使用前有个前提:界定清楚你要求的随机变量的目标和类型
4.1.1 求的是次数,还是数量?
条件期望和全期望公式,之所以不如条件概率和全概率公式那么好理解,是因为需要仔细理解好,要分析的问题里,目标--随机变量,到底是什么?
- 是希望知道多次随机之后,随机变量的数量?
- 是希望知道多次随机后达到某个状态所用的次数? 有点类几何分布
- 等等
4.1.2 确定你要求的目标变量
- 比如1个A有可能变成A,B,C,D对于的概率是0.5,0.2,0.2,0.1
- 那么如果我们有100个A,那么想问可以生成多少个D?
- 那么如果我们有100个A,那么想问可以生成多少个C?
- 如果我想合成1个D,需要多少次呢?
- 这都是不同的问题
4.2 例题1:计算出去的 时间= 步数 =次数,属于这一类问题
- 一个矿工被困矿井里,面前可以打开3个门,均等概率,1个门回到外面花费3小时,1个门回到现在地方花费5小时,1个门回到现在地方花费7小时,求问矿工回到外面平均需要时间?
- 设置X为矿工出去要花的时间
- E(X) = 1/3* 3+ 1/3* (E(X)+5)+1/3* (E(X)+7)
- 3 E(X) = 3+ E(X)+5 +E(X)+7
- E(X) = 15
4.3 例题3:求次数,计算几何分布的期望
如果丢硬币
假设正面成功概率p, 反面失败概率1-p,问直到成功1次的次数是多少?(同几何分布)
可以直接用几何分布的概率和期望公式计算
- 几何分布概率: pdf=p*(1-p)^n
- 几何分布期望次数: E(X)=1/p
也可以用 条件期望和全期望公式
令n为第1次出现正面的次数,而Y表示单次实验的正反情况
E(N) =P*E(N|Y=1) + (1-P)*E(N|Y=0)
- 显然 E(N|Y=1) =1,因为既然 Y=1了那就成功了,那么次数N也就=1
- 而因为Y=0了,已经多了1次,而每次试验都是独立了又开始重新试验E(N)所以E(N|Y=0) =1+E(N)
这就是递归的规律
- E(N) =P*1 + (1-P)*(1+E(N))
- E(N) =P +(1-P)+ (1-P)*E(N)
- E(N) =1+ (1-P)*E(N)
- E(N) =1/p
这也是一个递归的问题
4.4 例题3:求个数
如果丢硬币
假设正面成功概率p, 反面失败概率1-p,问直到丢100次,有几次是成功呢?(多少个正面?)
- 不适合几何分布,求最后1次成功的次数
- 不适合二项分布,是求成功K次的概率,而二项分布的期望是np, 是k所有不同取值时*对应概率求和,也不符合
- 但是可以用 条件期望和全期望公式
令n为出现正面的总次数,而Y表示单次实验的正反情况
E(N) =P*E(N|Y=1) + (1-P)*E(N|Y=0)
- 显然 E(N|Y=1) =1,因为既然 Y=1了那就成功了,那么次数N也就=1
- 而因为Y=0了,已经多了1次,而每次试验都是独立了又开始重新试验E(N)所以E(N|Y=0) =1+E(N)
这就是递归的规律
- E(N) =P*1 + (1-P)*(1+E(N))
- E(N) =P +(1-P)+ (1-P)*E(N)
- E(N) =1+ (1-P)*E(N)
- E(N) =1/p
这也是一个递归的问题
5 条件期望,全期望公式和 马尔可夫转移
求次数,求时间都可以用 条件期望,全期望公式等
求次数,用各种分布求,解方程求,用条件期望/全条件期望算
求概率,用马尔可夫可以解
用概率没法求
1/3* 3+ 1/3* (E(X)+5)+1/3* (E(X)+7)