题目:
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + ... + sn t = t1 + t2 + ... + tm |n - m| <= 1 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ... 注意:a + b 意味着字符串 a 和 b 连接。
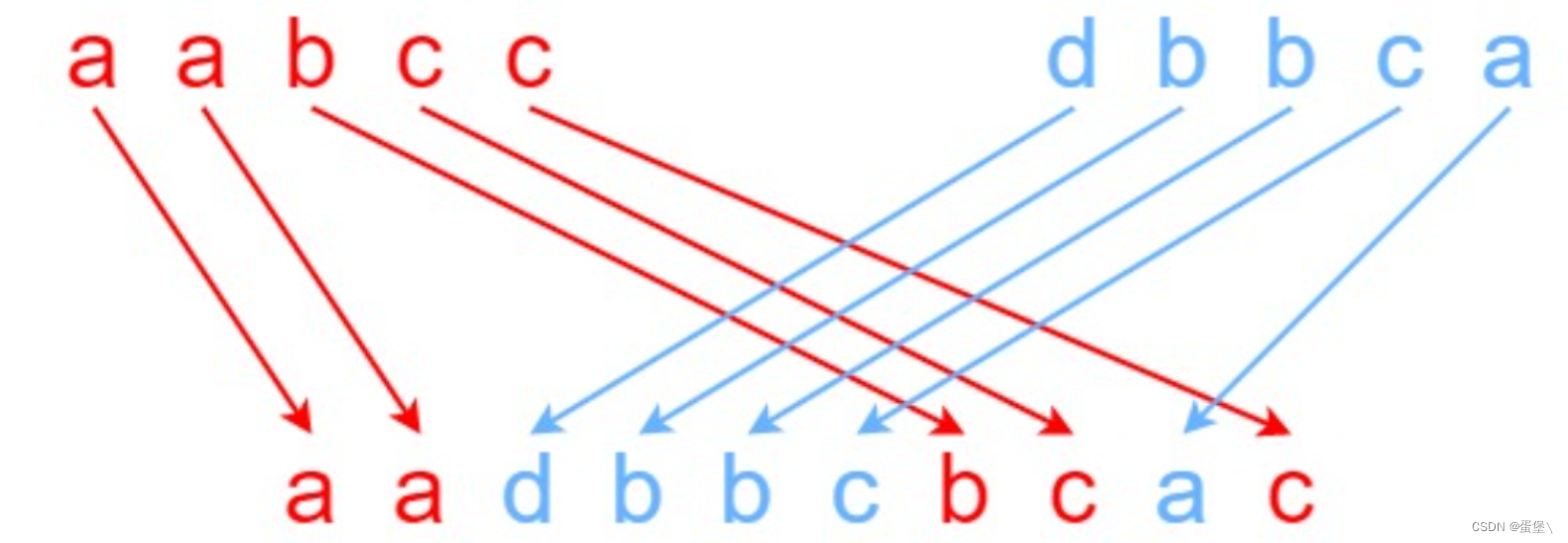
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出:true
解题思路:
本题采用动态规划来实现。
1.dp[i][j]表示由s1的前i个字符和s2的前j个字符组成的字符串是否可以交错组成s3的前i+j个字符
2.可分为三种情况:第0行、第0列、其他位置
3.在其他位置时,我们需要考虑的是s3[i+j-1]的字符是来自s1还是s2,所以两种情况都要写出来,满足任意一个即可。
如果s1的第i个字符和s3的第i+j个字符相等,并且s1的前i-1个字符和s2的前j个字符可以交错组成s3前i+j-1个字符,那么s1的前i个字符和s2的前j个字符可以交错组成s3的前i+j个字符;
dp[i-1][j] && (s1[i-1]==s3[i+j-1])
s2的第j个字符也是同理。dp[i][j-1] && (s2[j-1]==s3[i+j-1])
那么,s1和s2其中一个满足,那么dp[i][j]也符合题意,dp[i][j]=1
源代码如下:
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int len1=s1.size();//s1的长度
int len2=s2.size();//s2的长度
int len3=s3.size();//s3的长度
//若s1的长度加上s2的长度不等于s3的长度,很显然不能交错组成s3
if(len1+len2!=len3) return false;
//定义动态规划数组dp
//dp[i][j]表示由s1的前i个字符和s2的前j个字符组成的字符串是否可以交错组成s3的前i+j个字符
vector<vector<int>> dp(len1+1,vector<int>(len2+1));
dp[0][0]=1;//对dp[0][0]进行初始化
//先找到s3的起始位置是由哪个字符串组成的
// 第0列:s1前缀长度i + s2前缀长度0,能否交错组成s3前缀长度i
for(int i=1;i<=len1;i++)
{
if(s1[i-1]==s3[i-1])
{
dp[i][0]=dp[i-1][0];
}
else
{
dp[i][0]=0;
}
}
// 第0行:s1前缀长度0 + s2前缀长度i,能否交错组成s3前缀长度i
for(int j=1;j<=len2;j++)
{
if(s2[j-1]==s3[j-1])
{
dp[0][j]=dp[0][j-1];
}
else
{
dp[0][j]=0;
}
}
// 考虑s3的最后一个字符s3[i+j-1]来自s1的第i个字符还是s2的第j个字符
for(int i=1;i<=len1;i++)
{
for(int j=1;j<=len2;j++)
{
// 如果来自s1[i-1],则dp[i][j] 为:s1前缀长度i-1 + s2前缀长度j 能否交错组成s3前缀长度i+j-1,即:dp[i-1][j]
int flag1=dp[i-1][j]*(s1[i-1]==s3[i+j-1]?1:0);
// 如果来自s2[j-1],则dp[i][j] 为:s1前缀长度i + s2前缀长度j-1 能否交错组成s3前缀长度i+j-1,即:dp[i][j-1]
int flag2=dp[i][j-1]*(s2[j-1]==s3[i+j-1]?1:0);
if(flag1+flag2>0)
{
dp[i][j]=1;
}
else
{
dp[i][j]=0;
}
}
}
//返回结果,dp[len1][len2]为1,则返回true,为0则返回false
return dp[len1][len2];
}
};时间复杂度:O(len1*len2)
空间复杂度:O(len1*len2)