Git 就像个时光机器,能让我们还原到任何提交。
还原未提交的更改
假如我们在查看一个干净的代码仓库,干净意味着工作区中的文件保持着最后一次提交的状态,没有修改。在查看的过程中,我们有意或无意的修改了工作区中的文件,之后我们想把这些文件恢复成查看前的样子。像这样要还原自上次提交以来在工作区所做的所有更改,方法为:选中所有更改文件的父目录,鼠标右键单击,在弹出的上下文菜单中,选择 TortoiseGit - Revert 。

弹出还原对话框,在该对话框中,选择全部,单击 “OK” 键,自上次提交以来的所有修改会全部还原。这意味着工作区中的内容重新变得和最后一次提交时的内容一致。

注:
- 如果只是还原一个文件,可以选中该文件,鼠标右击 -
TortoiseGit - Revert - 如果要还原
已删除或重命名文件, 必须要选中父目录,鼠标右击 -TortoiseGit - Revert,这是因为工作区中已经找不到该文件了。 - 如果还原
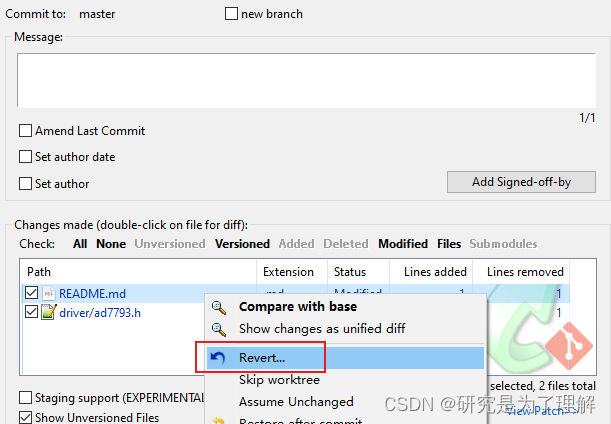
已删除、重命名和新添加文件,也可以在提交(commit)时、查看仓库状态(status)时选择相应文件,使用右键菜单 -Revert...。比如在提交对话框中,如果你发现README.md文件是意外修改的,你不想提交它,而是要把它恢复,这时只需要选中README.md文件,鼠标右击 -Revert...。
还原已提交的更改
上面的 Revert 操作只能还原本地工作区中的更改,如果要还原已经提交的更改,则需要在 日志对话框 中操作:
- 选中仓库,鼠标右击 -
Git Show log,打开日志对话框; - 选择要还原的提交,鼠标右击 -
Revert change by this commit,即可完成还原。如果你还原了最后一个提交,最后一个提交的信息仍然保留着,但工作区中最后一次提交修改的内容已经被还原; - 马上进行一次提交,或者修改工作区的内容后再提交。

注:虽然你还原了最后一次提交的修改,但是最后一次提交仍然会存在你的仓库中,并且可以在日志对话框中看到。
重置
如果你提交了几次后,出于某种原因,最近的几次提交不想要了,你想回到某个提交,就像最近的几次提交不存在一样。实现这种情景的是 重置(reset)。
重置仍然在日志对话框中操作。如下图所示,我想将某个仓库重置到“feat: 增加颜色区分AQI等级”提交:选中该提交,鼠标右击 - Reset "master" to this... 。

这将打开重置对话框,如下图所示:

这里有三种 重置类型 (Reset Type):
- Soft:软重置。之前的提交内容不删除,全部还原到工作区,这些文件处于
已暂存状态,通过 Git 命令可以看出:

- Mixed:混合重置。这是默认设置。之前的提交内容不删除,全部还原到工作区,这些文件处于
已修改状态,通过 Git 命令可以看出:

注:这里用到 Git 命令只是为了说明Soft模式 和Mixed模式的细微差别,之所以用 Git 命令,是因为除了叠加的图标, TortoiseGit 看不出来这两种模式的区别。换句话说,如果你使用 TortoiseGit ,你可以无视Soft模式 和Mixed模式的区别,使用任何一个都可以。 - Hard:硬重置。之前的提交内容全部删除,并不会还原到工作区。工作区只保留这次提交的内容,即“feat: 增加颜色区分AQI等级”提交的内容。
所以如果你确定不要某些提交,选择 硬重置 即可。
读后有收获,资助博主养娃 - 千金难买知识,但可以买好多奶粉 (〃‘▽’〃)