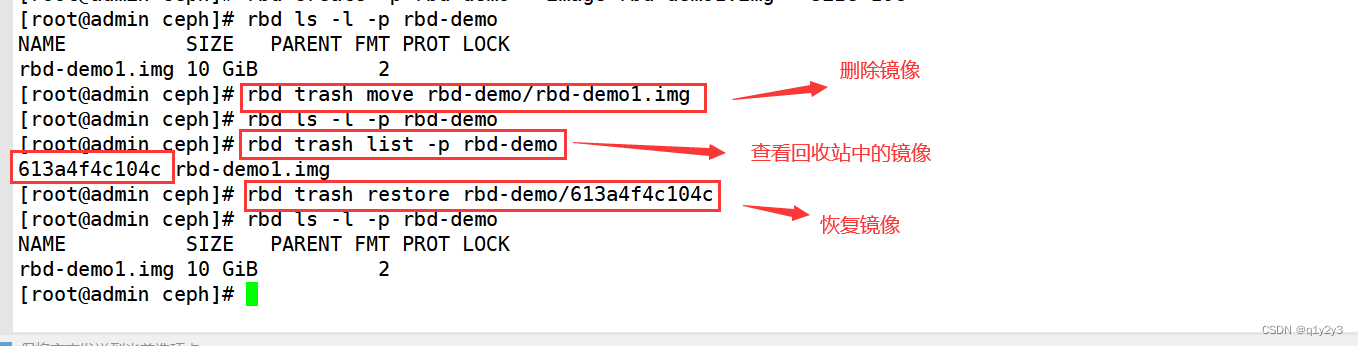
原文链接:https://mp.weixin.qq.com/s?__biz=Mzg4MjgxMjgyMg==&mid=2247486366&idx=2&sn=242bd062b6bcd1d32acba16a148f58c9&chksm=cf51b967f8263071d912a178881c7ff3c4143b78201c30723a8c121cc53f47ade584a918648c#rd
第三讲 相控阵雷达 与 “1+1=2”
主讲人:海军工程大学,刘涛教授
视频链接:【学报课堂 | 雷达系统微课 第三讲 相控阵雷达与“1+1=2”】 https://www.bilibili.com/video/BV1Gh4y1L7ty/?share_source=copy_web&vd_source=df7f4ac973cf1b719ee0d863f5ecf8f2
文章目录
- 第三讲 相控阵雷达 与 "1+1=2"
- 相控阵天线实现扫描的原理
- 空域采样和时域采样
- 波束宽度和天线增益 随 波束指向的变化趋势
- 波束宽度
- 天线增益
- 结论
- 相扫天线孔径渡越时间/填充时间
- 未来展望
-
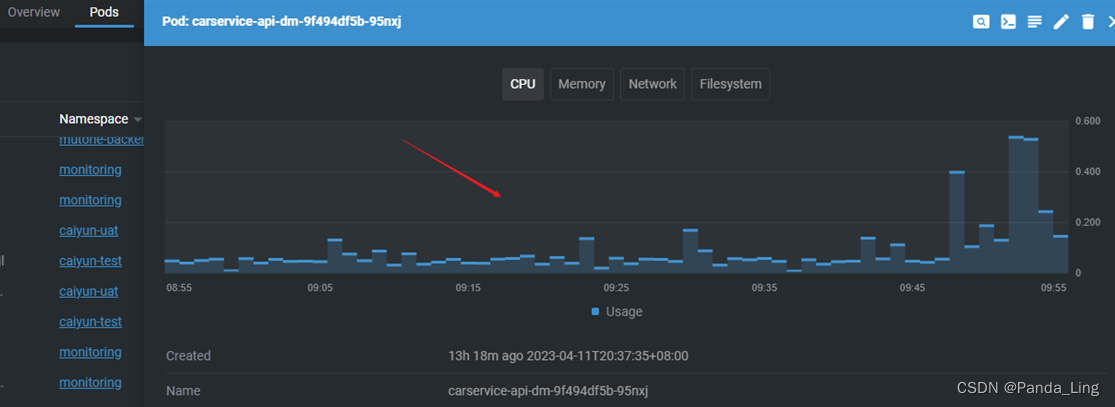
传统扫描体制单天线雷达面临的挑战
- 难以胜任 高空高速隐身目标 + 低空慢速小目标
-
相控阵雷达
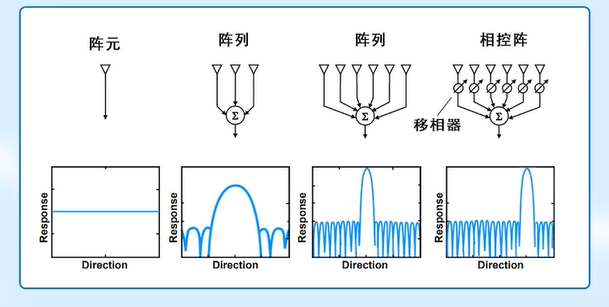
- 在发射端,通过移相器 或 数字波束形成,实现无惯性波束扫描
- 在接收端,对各个天线单元接收信号进行采样,转换为数字信号
- 从而实现更加灵活的波束控制
相控阵天线实现扫描的原理
-
在均匀线阵和远场假设下,发射天线

-
则,在偏离法线 θ \theta θ 方向的远场电场为:
- E ⃗ ( θ ) = ∑ k = 0 N − 1 E ⃗ k ( θ ) \vec{E}(\boldsymbol{\theta})=\sum_{k=0}^{N-1} \vec{E}_k(\boldsymbol{\theta}) E(θ)=∑k=0N−1Ek(θ)
-
以0号阵元为基准,则:
- E ⃗ ( θ ) = E 0 e j ⋅ ϕ 0 E ⃗ ( θ ) = E 0 e j ⋅ ϕ 0 ∑ κ = 0 N − 1 e j k ( ψ − ϕ ) \begin{aligned} & \vec{E}(\theta)=E_0 e^{j \cdot \phi_0} \\ & \vec{E}(\theta)=E_0 e^{j \cdot \phi_0} \sum_{\kappa=0}^{N-1} e^{j k(\psi-\phi)}\end{aligned} E(θ)=E0ej⋅ϕ0E(θ)=E0ej⋅ϕ0κ=0∑N−1ejk(ψ−ϕ)
- ϕ \phi ϕ: 移相器引入的滞后相位
- ψ \psi ψ:波程差带来的超前相位
-
由于波程差引起的相位差
- ψ = d sin θ λ ⋅ 2 π \psi=\frac{d \sin \theta}{\lambda} \cdot 2 \pi ψ=λdsinθ⋅2π
-
利用等比数列求和,得到合成电场:
- 首项为: E 0 e j ⋅ ϕ 0 E_0 e^{j \cdot \phi_0} E0ej⋅ϕ0
- 公比为 e j ⋅ ( ψ − ϕ ) e^{j \cdot (\psi-\phi)} ej⋅(ψ−ϕ)
- 最终的合成电场为: E → ( θ ) = E 0 e j ⋅ ϕ 0 1 − e j N ( ψ − ϕ ) 1 − e j ( ψ − ϕ ) = E 0 e j ⋅ ϕ 0 sin [ N ( ψ − ϕ ) / 2 ] sin [ ( ψ − ϕ ) / 2 ] e j N − 1 2 ( ψ − ϕ ) \begin{aligned} \overrightarrow{\boldsymbol{E}}(\boldsymbol{\theta}) & =\boldsymbol{E}_0 \boldsymbol{e}^{j \cdot \phi_0} \frac{1-e^{j N(\psi-\phi)}}{1-e^{j(\psi-\phi)}} \\ & =\boldsymbol{E}_0 \boldsymbol{e}^{j \cdot \phi_0} \frac{\sin [N(\psi-\phi) / 2]}{\sin [(\psi-\phi) / 2]} e^{j \frac{N-1}{2}(\psi-\phi)}\end{aligned} E(θ)=E0ej⋅ϕ01−ej(ψ−ϕ)1−ejN(ψ−ϕ)=E0ej⋅ϕ0sin[(ψ−ϕ)/2]sin[N(ψ−ϕ)/2]ej2N−1(ψ−ϕ)
-
可见,相控阵天线实现波束扫描的实质是:
-
只要改变移相器的值,就可以在不同的 θ \theta θ上获得最大增益值,这就实现了天线波束扫描
-
本质是:改变移相器的值,抵消阵元间波程差引起的相位差
✅ 从而实现某个方向上,电场矢量的同相叠加
-
- 也可以利用时间延迟线代替移相器
- 与 1+1=2 的思想一致
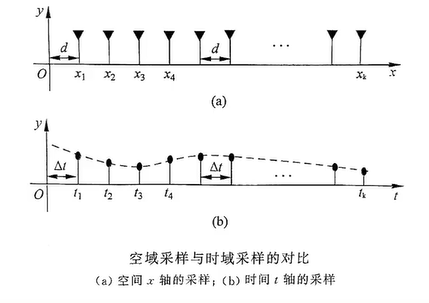
空域采样和时域采样
-
相控阵天线的阵列信号处理
-
实质上是空域信号处理
-
在不同空间位置采样
-
-
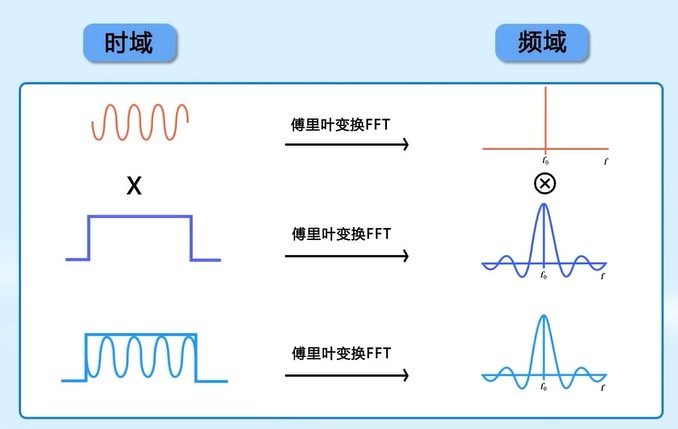
时域SP理论可推广到空域
-
信号阵列不能无限长 ⇒ \Rightarrow ⇒ 相当于时域加窗 ⇒ \Rightarrow ⇒ 所以会出现旁瓣泄露
-
天线间距过大 ⇒ \Rightarrow ⇒ 采样频率过低 ⇒ \Rightarrow ⇒ 角度估计空间模糊
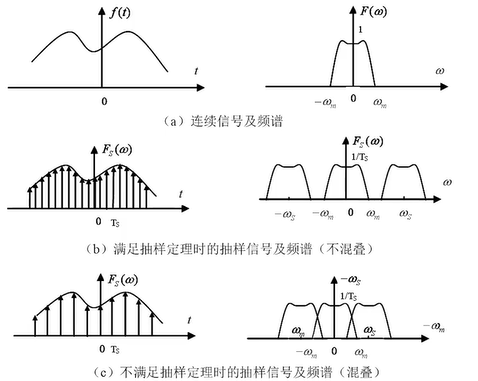
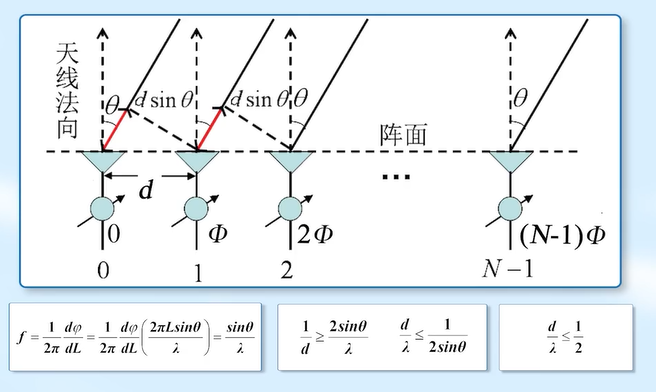
-
波束宽度和天线增益 随 波束指向的变化趋势
波束宽度
- 波束指向法线时
-
天线方向图如下
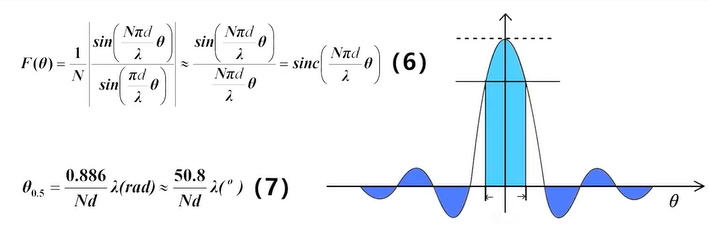
-
可得半功率波束宽度,与常规天线半功率波束宽度 λ / D \lambda / D λ/D基本一致 (D: 天线孔径)
-
- 当波束指向偏离法线时
-
天线主瓣宽度展宽
-
当阵列馈电不同相时,等效为同相阵面偏转
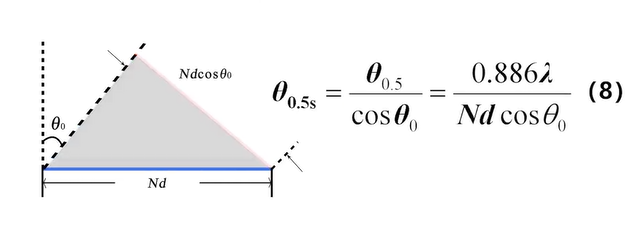
-
该结论还可以推广到面阵
-
天线增益
- 当波束指向法向:
-
天线增益表达式
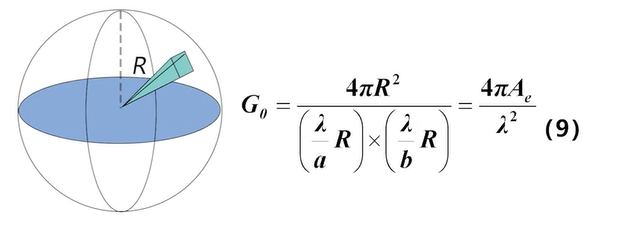
-
a b 为方位俯仰 天线孔径长度, A e Ae Ae为天线等效接收面积
-
- 当波束指向偏离法向时
-
有效孔径变为在 θ 0 \theta_0 θ0上的投影
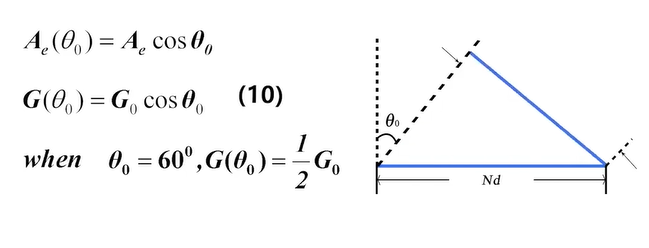
-
结论
- 当扫描角增加时
- 波束宽度也增加
- 天线增益下降
- 性能下降
一般要求波束扫描角 小于等于 60度
- 意味着 至少 3个 天线阵才能覆盖半球
相扫天线孔径渡越时间/填充时间
-
指阵列两端两个天线阵元所辐射信号,到达位于偏离法线 θ 0 \theta_0 θ0方向的同一目标的时间差
-
它应该足够小,以不影响各阵元处信号的包络
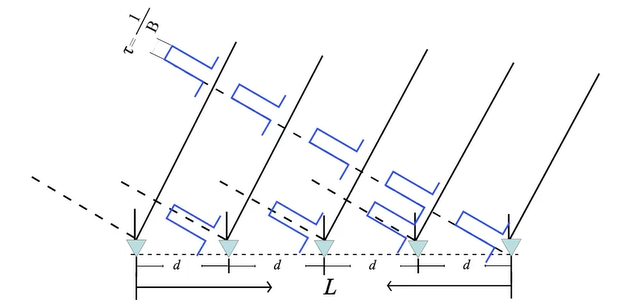
-
-
需满足 L / c ≤ τ = 1 / B L/c \leq \tau = 1/B L/c≤τ=1/B
- 其中L为阵列长度,
- 即 B L ≤ c BL \leq c BL≤c
- 因此信号带宽必须足够小 ⇒ \Rightarrow ⇒ 以使较大阵列能够相干叠加
-
宽带相控阵的解决方案
- 利用时间延迟线等方法减小对带宽的限制
未来展望
- 相控阵雷达的发展趋势:
- 数字阵列雷达
- MIMO雷达
- 频率分集雷达
- 分布式雷达等
- 但本质都没有脱离矢量同相相加