双指针算法指的是，从数组的两侧开辟指针变量进行查找，这类问题往往通过暴力（双循环）可以解出，而采用双指针相当于用空间换取时间，省略双层循环中重复的部分。

---

对于一个含有负数的有序数组，要求保证在该数组每个元素平方后仍然保证有序。

如：-7 1 6 6 ，则平方后的排序应该是：1 36 36 49

一个简单的想法是，将所有元素平方后再进行排序，这是一种比较暴力的做法，复杂度取决于排序算法的复杂度。

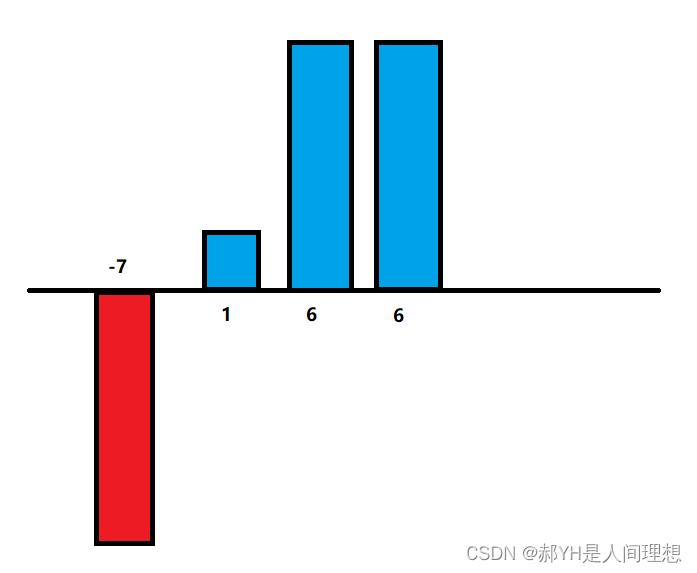
然而仔细思考一下不难发现，平方的本质就是二倍的绝对值，而绝对值是一种计算模长的方式：对对于向量来说，不考虑方向的情况下模长即为大小。对应本题，换句话说，由于原数组本身为有序数组，平方后的最大值一定出现在原数组的两端——最小的负数和最大的正数之间。

因此我们可以采用双指针算法，从数组两侧开始寻找，左右指针指向元素大的先压入新的数组，然后向中间移动指针，再进行下一轮比较；直到两指针相遇时结束~ 

具体的C++代码如下：

#include <iostream>
#include <vector>
 
using namespace std; 

int main(int argc, char** argv) {
	int num=0;
	vector<int> V;
	cout<<"请输入数组中元素的个数："<<endl;
	cin>>num;
	for(int i=1;i<=num;i++)
	{
		int temp=0;
		cin>>temp;
		V.push_back(temp);
	}
	cout<<"原数组为："; 
	for(vector<int>::iterator it=V.begin();it!=V.end();it++)
		cout<<(*it)<<" ";
	cout<<endl;
	
	int it1=0,it2=num-1;
	//分别指向头部和尾部
	vector<int> N;
	for(int i=1;i<=num;i++)
		N.push_back(0);
	//开辟新的数组用于存放平方后的数组 
	while(it1<=it2)
	{   //指针未相遇时持续循环 
		if(V[it1]*V[it1]>=V[it2]*V[it2])
		{
			//大者先入数组 
			int temp1=V[it1]*V[it1]; 
			N[num-1]=temp1;
			//直接将大的存在最后面，省去排序的过程 
			it1++;
			//指针向中间移动 
			num--;
			//下标要向前移动 
		}
		else if(V[it2]*V[it2]>V[it1]*V[it1])
		{
			int temp2=V[it2]*V[it2];
			N[num-1]=temp2;
			it2--;
			num--;
			//同理 
		}
	} 
	cout<<"升序后的平方和数组为："<<endl;
	for(vector<int>::iterator it=N.begin();it!=N.end();it++)
		cout<<(*it)<<" ";
	cout<<endl;
	return 0;
}

运行结果如下：

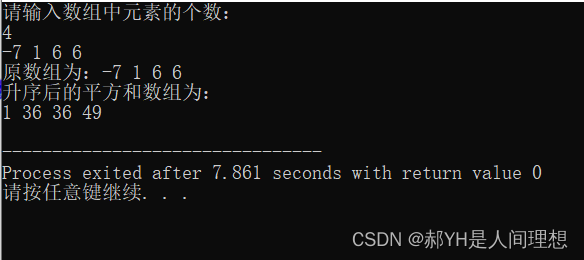
再加一组测试用例：-7 -3 1 1 5 9

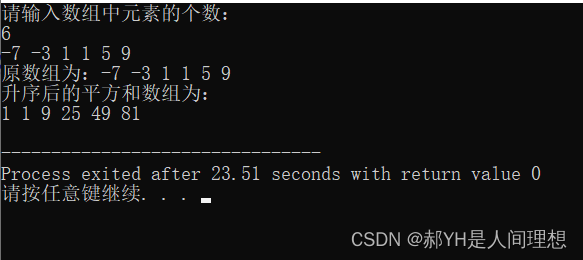
 答案符合预期~