【算法与数据结构】144、94、145LeetCode二叉树的前中后遍历（递归法、迭代法）

news2025/11/4 9:28:01

文章目录

  • 一、题目
  • 二、递归算法
  • 三、迭代算法
    • 3.1 迭代算法1
    • 3.2 迭代算法2 ——统一风格写法
  • 四、完整代码

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

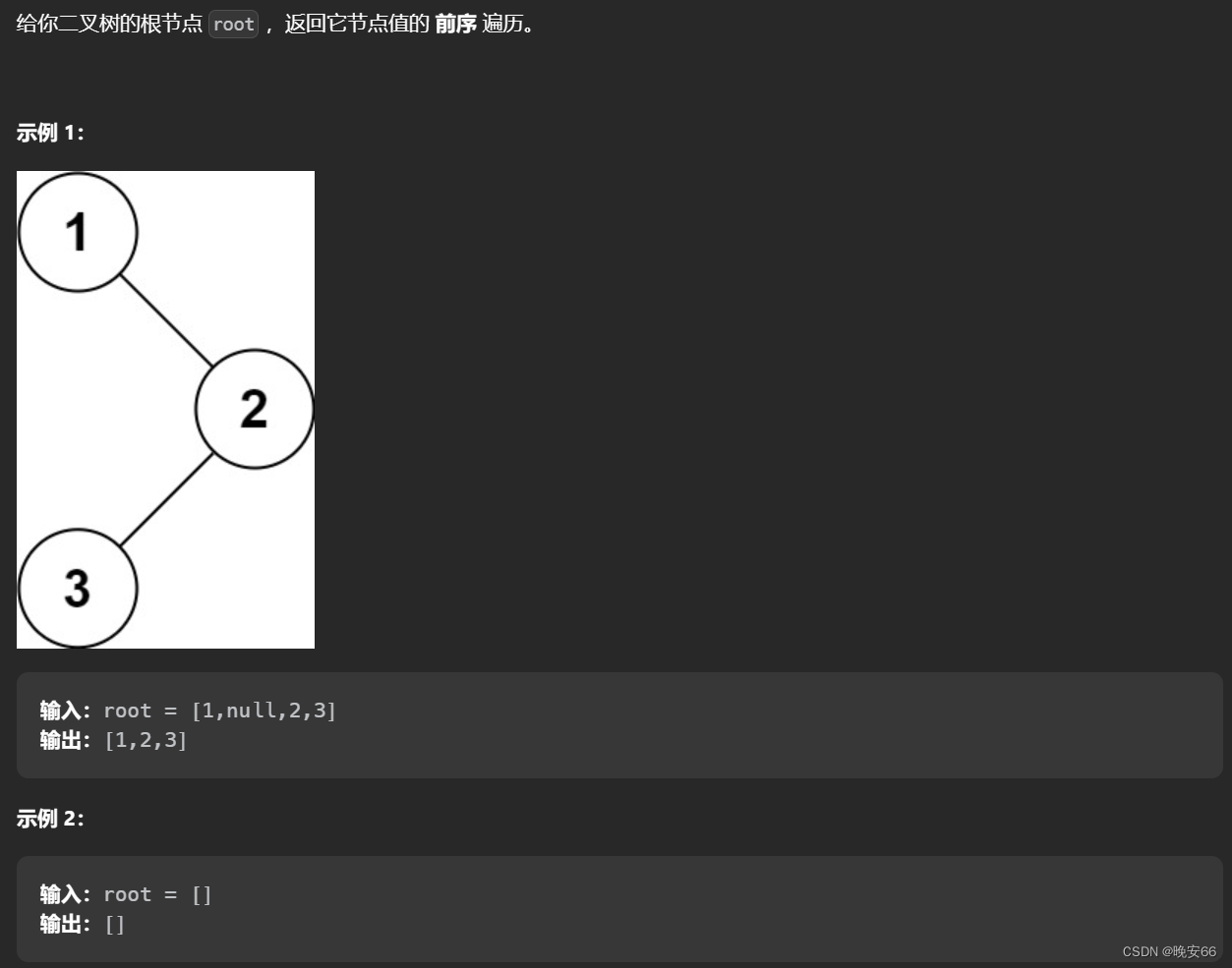
在这里插入图片描述
在这里插入图片描述

二、递归算法

  思路分析：这道题比较简单，不多说了，大家直接看代码就行。注意前中后遍历是指中间节点的遍历顺序。同时中序和后序的代码也很类似，这里给出三道题代码。前中后递归遍历算法对比下来，仅仅改变了一两行代码，就改变了结点的遍历顺序。
  前序遍历程序如下：

class Solution {
public:
    // 前序遍历
    void traversal_preOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);                // 中
        traversal_preOrder(cur->left, vec);     // 左
        traversal_preOrder(cur->right, vec);    // 右
    }

    vector<int> preorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        vector<int> result;
        traversal_preOrder(root, result);
        return result;
    }
};

复杂度分析可以参考这篇文章二叉树多种遍历的时间复杂度和空间复杂度。

  • 时间复杂度： O ( n ) O(n) O(n)。
  • 空间复杂度： O ( n ) O(n) O(n)。

  中序遍历程序如下：

// 中序遍历
class Solution2 {
public:  
    void traversal_midOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder(cur->left, vec);     // 左
        vec.push_back(cur->val);                // 中
        traversal_midOrder(cur->right, vec);    // 右
    }

    vector<int> inorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        vector<int> result;
        traversal_midOrder(root, result);
        return result;
    }
};

  后序遍历程序如下：

// 后序遍历
class Solution3 {
public:
    void traversal_postOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_postOrder(cur->left, vec);     // 左
        traversal_postOrder(cur->right, vec);    // 右
        vec.push_back(cur->val);                 // 中
    }

    vector<int> postorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        vector<int> result;
        traversal_postOrder(root, result);
        return result;
    }
};

三、迭代算法

3.1 迭代算法1

  遍历树节点的时候要注意是右节点先入栈，左节点后入栈，这样在出栈的时候就是左节点先出栈。
  前序遍历程序如下：

// 前序遍历迭代法 中左右
class Solution4 {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        stack<TreeNode*> st;
        vector<int> result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);    // 空节点不入栈
            if (node->left) st.push(node->left);      // 空节点不入栈，左节点后入栈，先出栈           
        }
        return result;
    }
};

  中序遍历是左中右，需要一层层找到最左边的节点，在遍历的过程当中依次将遍历元素压入栈，最左边元素就在栈顶，可以首先输出，就实现左中右顺序的遍历。
  中序遍历程序如下：

// 中序遍历迭代法 左中右
class Solution5 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        stack<TreeNode*> st;
        vector<int> result;
        TreeNode* node = root;
        while (node != NULL || !st.empty()) {   // 栈非空或节点非空, 每次循环更新node
            if (node != NULL) {
                st.push(node);
                node = node->left;
            }
            else {
                node = st.top();
                st.pop();
                result.push_back(node->val);
                node = node->right;    // 右节点
            }    
        }
        return result;
    }
};

  后序遍历只需要将前序遍历翻转一下就能实现。
  后序遍历程序如下：

// 后序遍历迭代法 左右中
class Solution6 {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left);    // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right);  // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

3.2 迭代算法2 ——统一风格写法

  在迭代算法1中，迭代法实现的先中后序，其实风格也不是那么统一，除了先序和后序，有关联，中序完全就是另一个风格了，一会用栈遍历，一会又用指针来遍历。因此这里我们选择用一种统一的风格来写前中后遍历的迭代算法。目的就是实现类似递归算法中改变一两行代码就能前中后遍历相互转换。
  迭代算法1中中序遍历使用栈实现，它无法解决访问节点和处理节点不一致的情况，也就是说中序遍历时。我们是先访问中节点，然后在访问右节点和左节点，但是处理时，是先处理左节点、然后才是中节点和右节点。为了解决这个问题，我们将要访问的节点放入栈中，把要处理的节点也放入栈中，同时做标记，表示已经入栈，但是还没有处理。代码如下，可以看出，前中后遍历都只改动了一两行代码。
  中序遍历程序如下：

// 中序遍历，统一代码风格迭代写法
class Solution7 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node->right) st.push(node->right);  // 添加右节点（空节点不入栈）
                st.push(node);                          // 添加中节点
                st.push(NULL);                          // 添加标记空指针，表示中结点访问过，但还没处理
                if (node->left) st.push(node->left);    // 添加左节点（空节点不入栈）
            }
            else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();                       // 将空节点弹出
                node = st.top();                // 重新取出栈中元素
                st.pop();
                result.push_back(node->val);    // 加入到结果集
            }
        }
        return result;
    }
};

  前序遍历程序如下：

// 前序遍历，统一代码风格迭代写法
class Solution8 {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                st.push(node);                          // 中
                st.push(NULL);
            }
            else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

  后序遍历程序如下：

// 后序遍历，统一风格迭代写法
class Solution9 {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
            }
            else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

四、完整代码

# include <iostream>
# include <vector>
# include <stack>
using namespace std;
// 树节点定义
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
// 前序遍历递归法
class Solution {
public:   
    void traversal_preOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);                // 中
        traversal_preOrder(cur->left, vec);     // 左
        traversal_preOrder(cur->right, vec);    // 右
    }

    vector<int> preorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        vector<int> result;
        traversal_preOrder(root, result);
        return result;
    }
};
// 中序遍历递归法
class Solution2 {
public:  
    void traversal_midOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_midOrder(cur->left, vec);     // 左
        vec.push_back(cur->val);                // 中
        traversal_midOrder(cur->right, vec);    // 右
    }

    vector<int> inorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        vector<int> result;
        traversal_midOrder(root, result);
        return result;
    }
};
// 后序遍历递归法
class Solution3 {
public:
    void traversal_postOrder(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        traversal_postOrder(cur->left, vec);     // 左
        traversal_postOrder(cur->right, vec);    // 右
        vec.push_back(cur->val);                // 中
    }

    vector<int> postorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        vector<int> result;
        traversal_postOrder(root, result);
        return result;
    }
};
// 前序遍历迭代法 中左右
class Solution4 {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        stack<TreeNode*> st;
        vector<int> result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);    // 空节点不入栈，右节点
            if (node->left) st.push(node->left);    // 空节点不入栈，左节点后入栈，先出栈           
        }
        return result;
    }
};
// 中序遍历迭代法 左中右
class Solution5 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        if (root == NULL) return {};
        if (root->left == NULL && root->right == NULL) return { root->val };
        stack<TreeNode*> st;
        vector<int> result;
        TreeNode* node = root;
        while (node != NULL || !st.empty()) {   // 栈非空或节点非空, 每次循环更新node
            if (node != NULL) {
                st.push(node);
                node = node->left;
            }
            else {
                node = st.top();
                st.pop();
                result.push_back(node->val);
                node = node->right;    // 右节点
            }    
        }
        return result;
    }
};
// 后序遍历迭代法 左右中
class Solution6 {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left);    // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right);  // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};
// 中序遍历，统一代码风格迭代写法
class Solution7 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node->right) st.push(node->right);  // 添加右节点（空节点不入栈）
                st.push(node);                          // 添加中节点
                st.push(NULL);                          // 添加标记空指针，表示中结点访问过，但还没处理
                if (node->left) st.push(node->left);    // 添加左节点（空节点不入栈）
            }
            else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();                       // 将空节点弹出
                node = st.top();                // 重新取出栈中元素
                st.pop();
                result.push_back(node->val);    // 加入到结果集
            }
        }
        return result;
    }
};
// 前序遍历，统一代码风格迭代写法
class Solution8 {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                st.push(node);                          // 中
                st.push(NULL);
            }
            else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};
// 后序遍历，统一风格迭代写法
class Solution9 {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
            }
            else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

void my_print(vector <int>& v, string msg)
{
    cout << msg << endl;
    for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {
        cout << *it << "  ";
    }
    cout << endl;
}

int main() {
    // 构造树
    TreeNode* node3 = new TreeNode(3);
    TreeNode* node2 = new TreeNode(2, node3, NULL);
    TreeNode* root = new TreeNode(1, NULL, node2);
    Solution7 s1;
    vector<int> result = s1.inorderTraversal(root);
    my_print(result, "中序遍历结果：");
	system("pause");
	return 0;
}

end

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/770195.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LCD—STM32液晶显示（2.使用FSMC模拟8080时序）

LCD—STM32液晶显示（2.使用FSMC模拟8080时序）

目录 使用STM32的FSMC模拟8080接口时序 FSMC简介 FSMC NOR/PSRAM中的模式B时序图 用FSMC模拟8080时序 重点&#xff1a;HADDR内部地址与FSMC地址信号线的转换&#xff08;实现地址对齐&#xff09; 使用STM32的FSMC模拟8080接口时序 ILI9341的8080通讯接口时序可以由STM32使…
阅读更多...
PHP要怎么学--【强撸项目000】

PHP要怎么学--【强撸项目000】

强撸项目 总目录在000集 文章目录 本系列校训学习资源的选择环境的问题本人推荐 PHP视频的知识点分析总结题外话 本系列校训 用免费公开视频&#xff0c;卷飞培训班哈人&#xff01;打死不报班&#xff0c;赚钱靠狠干&#xff01; 只要自己有电脑&#xff0c;前后项目都能搞&a…
阅读更多...
sqli-labs 堆叠注入 解析

sqli-labs 堆叠注入 解析

打开网页首先判断闭合类型 说明为双引号闭合 我们可以使用单引号将其报错 先尝试判断回显位 可以看见输出回显位为2&#xff0c;3 尝试暴库爆表 这时候进行尝试堆叠注入&#xff0c;创造一张新表 ?id-1 union select 1,database(),group_concat(table_name) from informatio…
阅读更多...
给你一个网站，你如何测试？

给你一个网站，你如何测试？

首先&#xff0c;查找需求说明、网站设计 等相关文档&#xff0c;分析测试需求。 制定测试计划&#xff0c;确定测试范围和测试策略&#xff0c;一般包括以下几个部分&#xff1a; 功能性测试&#xff1b;界面测试&#xff1b;性能测试&#xff1b;数据库测试&#xff1b;安全…
阅读更多...
AD如何查看PCB完成度？快来看这篇文

AD如何查看PCB完成度？快来看这篇文

在Altium Designer&#xff08;AD&#xff09;中&#xff0c;很多工程师通过使用Design Rule Check&#xff08;DRC&#xff0c;常用于检查PCB设计是否符合设计规范和要求&#xff09;功能来检查PCB设计的完成度&#xff0c;但很多小白不太熟悉怎么去使用DRC&#xff0c;下面来…
阅读更多...
深入浅出C语言—【函数】下

深入浅出C语言—【函数】下

目录 5. 函数的嵌套调用和链式访问5.1嵌套调用5.2 链式访问 6. 函数的声明和定义6.1 函数声明6.2 函数定义 7. 函数递归&#x1f451;7.1 什么是递归&#xff1f;7.2 递归的两个必要条件7.2.1 练习17.2.2 练习2 7.3 递归与迭代7.3.1 练习37.3.2 练习4 5. 函数的嵌套调用和链式访…
阅读更多...
解决Missing cookie ‘JssionId‘ for method parameter of type String问题

解决Missing cookie ‘JssionId‘ for method parameter of type String问题

错误描述如下所示&#xff1a; 上述错误是我在使用CookieValue注解&#xff0c;获取cookieID时出现的&#xff0c;错误原因是由于**CookieValue注解注解中的value值和浏览器中的cookie的jssionID不一致所导致的** 如下所示为浏览器中的CookieID的参数名 而我在注解中写的如下图…
阅读更多...
浪涌保护器行业应用防雷选型方案

浪涌保护器行业应用防雷选型方案

当今社会中&#xff0c;电气设备的使用范围越来越广泛&#xff0c;也越来越普及&#xff0c;而与之相关的浪涌保护器就显得尤为重要。在这个领域&#xff0c;有一种高品质的浪涌保护器 —— 地凯防雷SPD浪涌保护器&#xff0c;它可以为各种设备提供强大的保护&#xff0c;并在各…
阅读更多...
YOLOv5——pytorch环境搭建

YOLOv5——pytorch环境搭建

环境搭建是一个最最基础而又基本的事情&#xff0c;是一切工作开始前的基本要求。 由于YOLOv7和YOLOv5不兼容&#xff0c;这次用到了YOLOv5&#xff0c;我不得不再使用anaconda创建一个虚拟环境。 Tip&#xff1a;很多人不了解Anaconda存在的意义&#xff0c;就是为了弥补pyt…
阅读更多...
四、DML-1.数据操作-添加

四、DML-1.数据操作-添加

一、DML介绍 Data Manipulation Language 数据操作语言 用来对数据库中表的数据记录进行增删改操作。 二、添加数据 1、给指定字段添加数据 insert into employee(id, workno, name, gender, age, idcard,entrydate) values (1, 001,Itcast, 男, 18, 123456789012345678, 2…
阅读更多...
kaggle新赛：学生摘要评估大赛赛题解析（NLP）

kaggle新赛：学生摘要评估大赛赛题解析（NLP）

赛题名称&#xff1a;CommonLit - Evaluate Student Summaries 赛题链接&#xff1a; https://www.kaggle.com/competitions/commonlit-evaluate-student-summaries/ 赛题背景 摘要写作是所有年龄段学习者的一项重要技能。总结可以增强阅读理解能力&#xff0c;特别是在第二…
阅读更多...
SOLIDWORKS工程图模板如何设置？

SOLIDWORKS工程图模板如何设置？

SOLIDWORKS工程图模板是非常重要的&#xff0c;它可以帮助工程师快速创建符合公司规范的工程图纸。本文将介绍SOLIDWORKS工程图模板的基本知识&#xff0c;包括如何创建和使用模板。 一、创建SOLIDWORKS工程图模板 首先&#xff0c;我们需要打开SOLIDWORKS软件&#xff0c;并选…
阅读更多...
MySQL高阶语句之二

MySQL高阶语句之二

目录 ​编辑 一、子查询 1.1语法 1.2select 1.3insert 1.3update 1.4delete 1.5 exists 1.6别名as 二、MySQL视图 2.1功能 2.2区别 2.3联系 2.4 创建视图(单表) 2.5 创建视图(多表) 2.6修改原表数据 2.7修改视图数据 三、NULL值 一、子查询 子查询也被称作内查询…
阅读更多...
虚拟机ubuntu1804打开联合标定工具箱的步骤（toolkit）

虚拟机ubuntu1804打开联合标定工具箱的步骤（toolkit）

1、运行roscore roscore 2、进入到calibration文件夹打开终端 source devel/setup.bash3、运行rosrun打开即可 rosrun calibration_camera_lidar calibration_toolkit
阅读更多...
iview的表格添加筛选功能需要注意的问题

iview的表格添加筛选功能需要注意的问题

给table的某列添加筛选功能 在table中通过给columns数据的项&#xff0c;设置 filters&#xff0c;可进行筛选&#xff0c;filters 接收一个数组。 然后再指定一个筛选函数 filterMethod 才可以进行筛选&#xff0c;filterMethod 传入两个参数value和 row。 如果指定 filter…
阅读更多...
基于异步FIFO的串口回环测试

基于异步FIFO的串口回环测试

文章目录 前言一、异步FIFO简介二、串口简介2.1 数据接收模块(RX)2.1 数据发送模块(TX) 三、IP核说明与配置2.1 PLL IP核2.2 FIFO IP核 四、数据关联 前言 当涉及到串口通信的硬件设计和软件开发时&#xff0c;进行有效的测试是至关重要的。串口回环测试是一种常见的测试方法&a…
阅读更多...
GSV6201替代方案|CS5466设计资料|CS5466原理图|typec转HDMI_8k方案芯片

GSV6201替代方案|CS5466设计资料|CS5466原理图|typec转HDMI_8k方案芯片

GSV6201是一款高性能、低功耗、高性能的&#xff0c;USB Type-C备用模式显示端口1.4至HDMI 2.1转换器。通过集成增强型微控制器&#xff0c;GSV6201创造了一个经济高效的解决方案提供了上市时间优势。显示端口接收机支持高达32.4Gbps&#xff08;HBR3&#xff0c;4通道&#xf…
阅读更多...
美国SaaS管理平台Zluri完成2000万美元的B轮融资

美国SaaS管理平台Zluri完成2000万美元的B轮融资

来源&#xff1a;猛兽财经 作者&#xff1a;猛兽财经 猛兽财经获悉&#xff0c;SaaS运营(SaaSOps)平台Zluri今日宣布获得2000万美元的融资&#xff0c;帮助企业管理SaaS资产并降低风险。B轮融资由Lightspeed领投&#xff0c;参与融资的其他投资者包括MassMutual Ventures、End…
阅读更多...
python 数学 中负数的取余的区别

python 数学 中负数的取余的区别

😄 今天发现python中负数的取余操作和数学中的是有区别的，在此记录一下。 文章目录 1、python中负数取余:2、数学中负数取余：3、总结：1、python中负数取余: res = a%b, 例子： -5%7=25%-7=-2-5%-7=-5如果a或b是负数，python则是会让商尽可能的小(即采用的是向下取整的方…
阅读更多...
JVM中的堆和栈到底存储了什么

JVM中的堆和栈到底存储了什么

JVM数据区 先上一张Java虚拟机运行时数据区中堆、栈以及方法区存储数据的概要图&#xff0c;如下所示&#xff1a; 然后我们来具体解析一下堆和栈 堆 堆是存储时的单位&#xff0c;对于绝大多数应用来说&#xff0c;这块区域是 JVM 所管理的内存中最大的一块。线程共享&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023