目录
A (1). Sum 详细点击:sum //整除分块
B (2). Sort
C (3). String //字符串dp
D (4). Factor //素数筛变式
E (5). Tree //树形dp
F (6). Geometry //几何
G (7). Graph //二分答案
H (8). Line //贪心
I (9). And / Or //位运算
J (10). Mov //模拟
A (1). Sum 详细点击:sum
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
ll T,x,y;
void solve() {
ll res=0;
cin>>x>>y;
ll i=min((ll)sqrt(x),y);
while(i*i+i+1>x)
i--;
res=(1+i)*i/2;
for(ll l=i+1,r; l<=y,l+1<=x; l=r+1) {
r=x/(x/(l+1))-1;
r=min(r,y);
if(l>r)
break;
res+=x/(l+1)*(r-l+1);
}
cout<<res<<"\n";
}
int main() {
IOS;
cin>>T;
while(T--)
solve();
return 0;
}B (2). Sort
使用stable_sort强行卡过,优化可了解:sort 学长Ashy深情讲解
#include<bits/stdc++.h>
using namespace std;
struct node {
long long x,y;
} d[100001];
long long e[100001];
long long n,q,t,u,v;
bool cmp(node a,node b) {
return a.x==b.x?a.y<b.y:a.x<b.x;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>q;
for(long long i=1; i<=n; i++)
cin>>d[i].x,d[i].y=i;
/*
for(int i=1; i<=n; i++)
cout<<d[i].x<<" "<<d[i].y<<"\n";
*/
stable_sort(d+1,d+1+n,cmp);
for(int i=1; i<=n; ++i)
e[d[i].y]=i;
while(q--) {
cin>>t;
if(t==1) {
cin>>u>>v;
d[e[u]].x=v;
stable_sort(d+1,d+1+n,cmp);
for(int i=1; i<=n; ++i)
e[d[i].y]=i;
} else {
cin>>u;
cout<<e[u]<<"\n";
}
}
return 0;
}在这提一下stable_sort和sort的区别,单纯从性能来讲sort性能更好,因为stable_sort要维护数据的稳定性,丧失了一部分性能,但在大部分数据顺序不变的情况下,stable_sort要比sort快很多
C (3). String
字符串dp,即区间dp
#include<bits/stdc++.h>
using namespace std;
//最长回文串子序列
int n;
string s;
int dp[2100][2100];
//字符串s在区间[i, j]范围内的最长回文子序列的长度
//dp[i][j] = dp[i+1][j-1] + 2;
//dp[i][j] = (dp[i+1][j] > dp[i][j-1]) ? dp[i+1][j] : dp[i][j-1];
int main() {
cin>>n>>s;
for (int i=0;i<n;i++)
dp[i][i]=1;
for (int len=2;len<=n;len++) {
for (int i=0;i<=n-len;i++) {
int j=i+len-1;
if (s[i]==s[j]) {
dp[i][j]=dp[i+1][j-1] + 2;
} else {
dp[i][j]=(dp[i+1][j]>dp[i][j-1])?dp[i+1][j]:dp[i][j-1];
}
}
}
cout<<n-dp[0][n-1];
return 0;
}D (4). Factor
用埃式筛暴力筛出来的,时间复杂度为O(nlogn)
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+1;
int n,a,ans;
bool vis[maxn];
int main() {
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1; i<=n; i++)
cin>>a,vis[a]=true;
for(int i=1; i<=maxn; i++)
for(int j=i; j<=maxn; j+=i)
if(vis[j]) {
ans++;
break;
}
cout<<ans;
return 0;
}
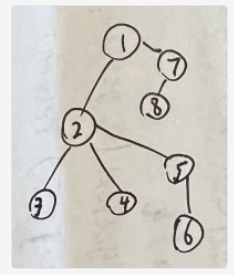
E (5). Tree
树形DP模板题
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e6+10;
ll a[N],u,v;
ll f[N],tot;
struct Edge {
int to,next;
} edges[N];
int head[N],edge_len,n;
void Add(int from,int to) {
edges[++edge_len].next=head[from];
edges[edge_len].to=to;
head[from]=edge_len;
}
void Dfs(ll e,ll fa) {
bool flag=0;
f[e]+=a[e];
for(int i=head[e]; ~i; i=edges[i].next) {
if(edges[i].to!=fa) {
flag=1;
Dfs(edges[i].to,e);
f[e]+=f[edges[i].to];
}
}
}
int main() {
memset(head,-1,sizeof head);
cin>>n;
for(int i=1; i<=n; i++)
cin>>a[i],tot+=a[i];
for(int i=1; i<n; i++) {
cin>>u>>v;
Add(u,v);
Add(v,u);
}
Dfs(1,0);
ll mx=0;
for(int i=2; i<=n; i++)
mx=max(mx,abs(f[i]-(tot-f[i])));
cout<<mx;
}F (6). Geometry
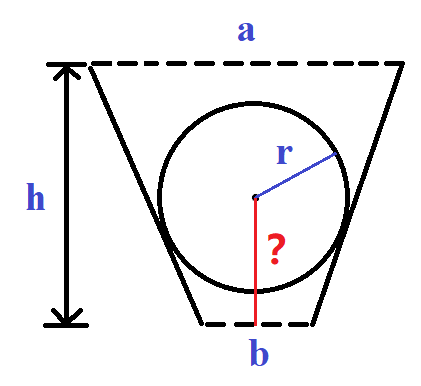
把梯形补成三角形
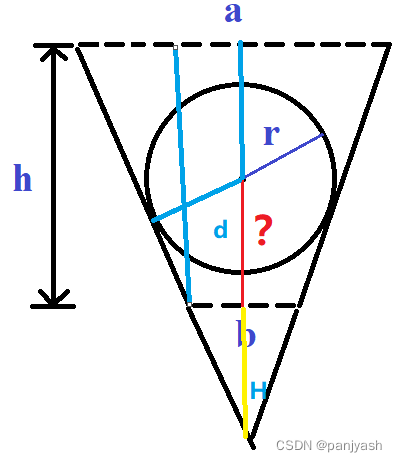
补出来的三角形与等腰三角形是相似三角形,通过三角形相似我们可以得出来
通过以上三式解方程就可以了。
#include<bits/stdc++.h>
using namespace std;
//梯形补成三角形
//按照比求三角形高与H圆心到三角形顶点的距离d+H
//H=b/(a-b)*h
//c=r*h*2/(a-b)
//d+H=sqrt(c*c+r*r)
double r,a,b,c,h,H,d;
int main() {
cin>>r>>a>>b>>h;
if(2*r<b){
cout<<"Drop";
return 0;
}
H=b/(a-b)*h*1.0;
c=r*h*2.0/(a-b);
d=sqrt(c*c+r*r)-H;
cout<<"Stuck\n";
cout<<fixed<<setprecision(7)<<d;
return 0;
}G (7). Graph
二分答案,judge函数用于判断给定的时间t是否满足从起点x到终点y的路径存在。
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
typedef long long ll;
int n,m,x,y;
int head[N],edge_len;
struct edge {
int next,to;
ll w;
} edges[N];
int u[N],v[N],w[N];
bool vis[N];
void Add(int from,int to,ll w) {
edges[++edge_len].next=head[from];
edges[edge_len].to=to;
edges[edge_len].w=w;
head[from]=edge_len;
}
void Dfs(int e) {
if(vis[e])
return;
vis[e]=true;
for(int i=head[e]; ~i; i=edges[i].next) {
if(!vis[edges[i].to])
Dfs(edges[i].to);
}
}
bool judge(int t) {
for(int i=0;i<=n;++i)
head[i]=-1,vis[i]=false;
edge_len=0;
for(int i=0; i<m; ++i) {
Add(u[i],v[i],w[i]);
if(w[i]>t)
continue;
Add(v[i],u[i],w[i]);
}
Dfs(x);
return vis[y];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m>>x>>y;
for(int i=0; i<m; ++i)
cin>>u[i]>>v[i]>>w[i];
int l=0,r=1e9,mid;
while(l<r) {
mid=l+r>>1;
if(judge(mid))
r=mid;
else
l=mid+1;
}
cout<<l<<"\n";
return 0;
}H (8). Line
贪心的思想,按边的右端点排序,以第一个右端点向右扩大k,找到第一个超出此范围的左端点,并将其右端点作为新的lc
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,k,cnt;
struct node {
ll l,r;
} d[1000001];
bool cmp(node a,node b) {
return (a.r==b.r)?a.l<b.l:a.r<b.r;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>k;
for (int i=0; i<n; i++)
cin>>d[i].l>>d[i].r;
sort(d,d+n,cmp);
ll lr=d[0].r+k;
for (int i=1; i<n; i++) {
if(d[i].l<=lr){
continue;
}
lr=d[i].r+k;
cnt++;
}
cout<<cnt+1;
return 0;
}I (9). And / Or
我们知道按位或是不进位加法, 恒成立。
因此只要把每个数进行按位与操作就可以得到最大值
#include<bits/stdc++.h>
using namespace std;
int n,a[100001],ans;
int main() {
cin>>n;
for(int i=1; i<=n; i++) {
cin>>a[i];
ans|=a[i];
}
cout<<ans;
return 0;
}J (10). Mov
模拟题,没啥好说的
#include<bits/stdc++.h>
using namespace std;
int n;
string s,t;
int a[1000001];
int main() {
cin>>n;
while(n--) {
cin>>s>>t;
//cout<<t;
int x=0;
if(s[0]=='C')
continue;
if(s[0]=='M') {
int i;
for(i=0; t[i]!=','; i++)
x=x*10+t[i]-'0';
if(t[i+1]<'0'||t[i+1]>'9') {
int y=0;
for(int j=i+2; j<t.size(); j++)
y=y*10+t[j]-'0';
if(t[i+1]=='#')
a[x]=y;
if(t[i+1]=='!')
a[x]=a[y];
if(t[i+1]=='@')
a[x]=a[a[y]];
} else {
int y=0;
for(int j=i+1; j<t.size(); j++)
y=y*10+t[j]-'0';
a[x]=a[y];
}
//cout<<a[x]<<"\n";
} else {
int y=0;
for(int i=0; i<t.size(); i++)
y=y*10+t[i]-'0';
cout<<a[y]<<"\n";
}
}
return 0;
}