注意事项:
本题为"树形DP—树的最长路径"的近似题,同时涉及到 单链表模拟邻接表存储图 的操作,建议先理解那篇文章。
题目:
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
1≤n≤10000,1≤ai,bi≤n,1≤ci≤105
输入:
5
2 1 1
3 2 1
4 3 1
5 1 1
输出:
2
#include <cmath>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
using namespace std;
const int N = 10010, M = N*2, INF = 0x3f3f3f3f; //无向边,M开点数的两倍
int n;
int h[N], e[M], ne[M], w[M], idx = 0; //邻接表链表模拟
int d1[N], d2[N], p1[N], up[N]; //d1[i]为点i向下的最长路径的长度,d2[i]为次长路径的长度,p1[i]为点i的最长路径的下一个点是谁,u[i]为点i向上的最长路径的长度
//经典的邻接表-链表模拟 存储图/树
void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
//向下找最长路径和次长路径,用子节点信息更新父节点,并返回最长路径的长度
int dfs_down(int u, int father) {
//遍历所有点,找到从u点向下走的最长路径和次长路径
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (j == father) continue; //向下找,所以不能向父节点找路
int d = dfs_down(j, u) + w[i]; //求出从u点向j点走,再向其他点走的最长路径的长度
//判断当前的这条路径是否能替换最长路径或者次长路径,并更新p1数组进行记录最长路径的下一个点
if (d >= d1[u]) {
d2[u] = d1[u], d1[u] = d;
p1[u] = j;
}
else if (d > d2[u]) {
d2[u] = d;
}
}
return d1[u];
}
//还是向下遍历树,但这次是用当前点u来更新点j的状态,也就是父节点信息更新子节点
void dfs_up(int u, int father) {
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (j == father) continue;
//如果点u的最长路径的下一个点(p1[u])是点j,那么就不能选最长路径来更新
if (p1[u] == j) up[j] = max(up[u], d2[u]) + w[i];
else up[j] = max(up[u], d1[u]) + w[i];
dfs_up(j, u);
}
}
int main() {
//读入
cin >> n;
memset(h, -1, sizeof h); //所有链表初始都指向-1
for (int i = 0; i<n-1; i++) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c); //无向边,那就a->b,b->a双向边即可
}
dfs_down(1, -1);
dfs_up(1, -1);
//枚举所有点的向上和向下的情况,求出最短距离
int res = INF;
for (int i = 1; i<=n; i++) {
res = min(res, max(d1[i], up[i]));
}
cout << res;
}
思路:
这个题和"树的最长路径"很相似,“树的最长路径”是只要求出 点向下的最长和次长路径的长度相加即可,
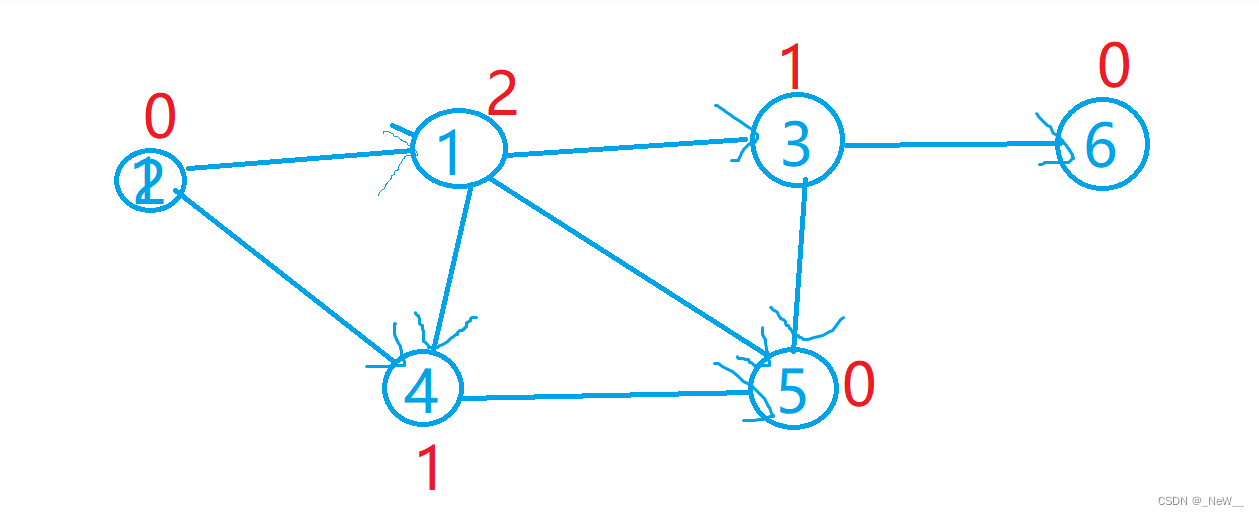
而这道题多了一种向上找路径的可能,那么不妨举个例子,还是和上题一样,将整个树“拎起来”,类似拓扑结构:
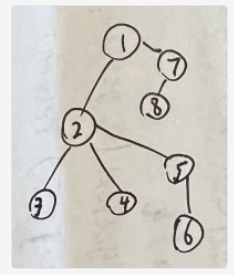
接下来以p1代表点一,p2代表点2
假设现在遍历到了p2,那如何求出p2到所有点的最长路径的长度?
条件1. 从当前节点往下,直到子树中某个叶节点的最长路径。
将p2能到的每条路(除了父节点p1)都dfs一遍即可。
条件2. 从当前节点往上走到其父节点,再从其父节点出发且不回到该节点的最长路径。
还是从上往下遍历,但这次是用p1来更新p2,首先判断p1的向下最长路径是否经过p2,
1.如果未经过p2,那么就可以直接更新p2的向上最长路径,也就是p1到p2的距离+p1的最长向下路径的长度,
2.如果经过p2,那么就说明p1的向下最长路径经过p2,也就不能使用最长路径了,这也就是为什么需要求出次长路径的原因,接着更新p2的向上最长路径,也就是p1到p2的距离+p1的次长向下路径的长度。
对所有的点进行上述两个条件的计算,再取max即为这个点到所有点的最长距离,
再将每个点的这个结果取min,即为树中某节点到其他所有节点最远距离最近的答案。
如果有所帮助请给个免费的赞吧~有人看才是支撑我写下去的动力!
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流