已知现在有几根柱子成有序排列，求出两根柱子之间围成面积的最大值。

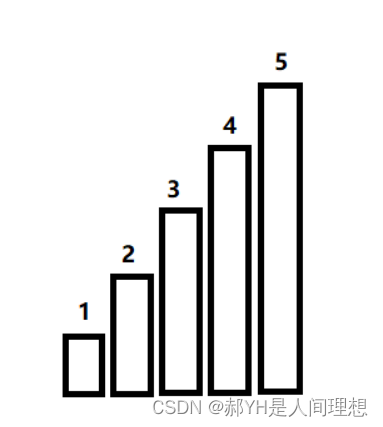
         不难想到，只需要将每两个柱子之间的面积计算一次并找出最大值，即可找到答案，但采用双指针法可以有效降低重复计算：从数组的两侧开始移动左右两个指针，首先计算当前面积，由于面积由两根柱子之间的短者决定，因此不难想出：下次移动较长的柱子所对应的指针是没有意义的，故我们应该移动较短侧的指针，如果移动后值变大则更新最大值，否则继续向前移动，直至两指针相遇——通过此种方法的复杂度为o（n）。

实现的代码如下：

#include <iostream>
#include <vector>
using namespace std;
 
int main(int argc, char** argv) {
	int num=0;
	vector<int> V;
	cout<<"请输入柱子的个数："<<endl;
	cin>>num;
	for(int i=1;i<=num;i++)
	{
		int temp=0;
		cin>>temp;
		V.push_back(temp);
	}
	cout<<"用户读入的数据为："; 
	for(vector<int>::iterator it=V.begin();it!=V.end();it++)
		cout<<(*it)<<" ";
	cout<<endl;
	cout<<endl;
	 
	int it1=0;
	int it2=num-1;
	//分别定义指向头尾的指针
	int max=0;
	while(it1!=it2)
	{
		cout<<"当前指针下标为："<<it1<<" and "<<it2<<endl;
		if(V[it1]>V[it2])
		{
			cout<<"左指针更大一些"<<endl;
			int maxt=(it2-it1)*V[it2];
			if(maxt>max)
				max=maxt;
			cout<<"本次操作的面积为："<<maxt<<endl;
			cout<<"当前操作的最大值为："<<max<<endl;
			it2--; 
		}
		else if(V[it2]>V[it1])
		{
			cout<<"右指针更大一些"<<endl;
			int maxt=(it2-it1)*V[it1];
			if(maxt>max)
				max=maxt;
			cout<<"本次操作的面积为："<<maxt<<endl;
			cout<<"累计操作的最大值为："<<max<<endl;
			it1++; 
		}
		cout<<endl;
	} 
	cout<<"求得的最大面积为："<<max<<endl; 
	return 0;
}

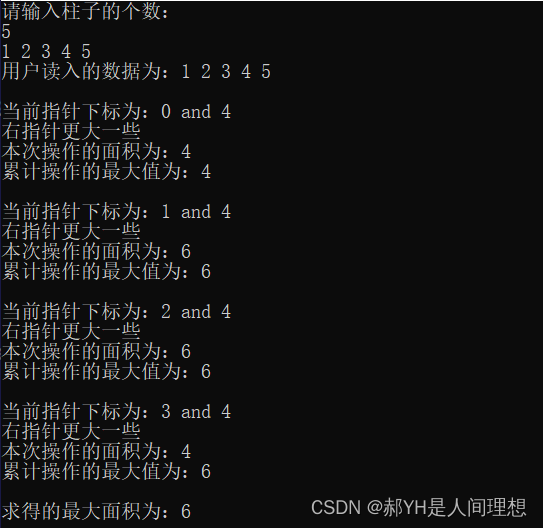
 通过手算不难发现上述用例结果为6。

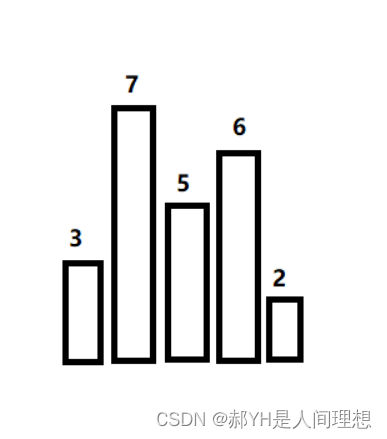
第二个用例，手算结果为12。

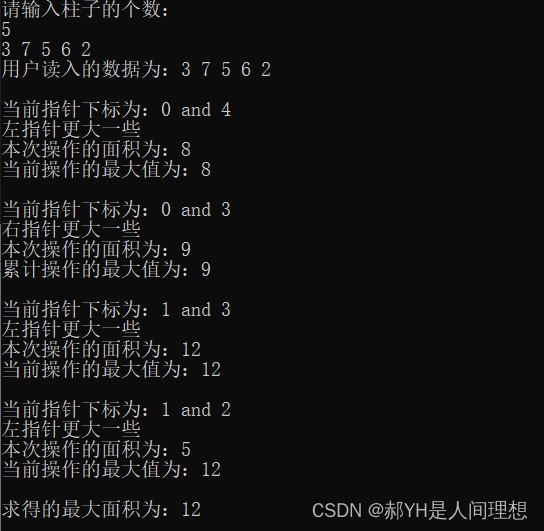
最后再来一个更长的用例，手算结果为42。

 

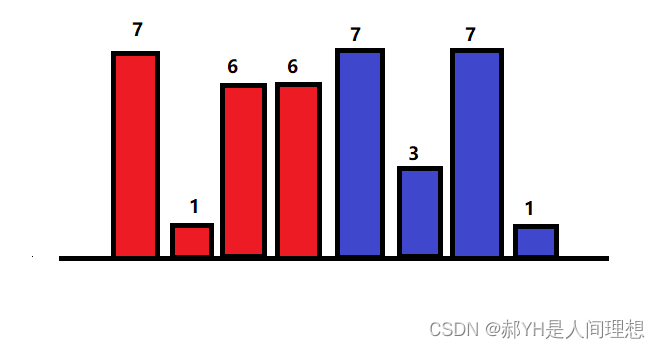
 此处发现了一个bug：就是源代码未考虑两个指针相等的情况。此处规定：当两指针相等时，对比两指针靠内侧的的下一位大小，如果左边大就移动左边，反之则右边，如果还相同则可以任选。

具体代码如下：

else if(V[it1]==V[it2])
		{
			cout<<"两个指针一样大"<<endl;
			int maxt=(it2-it1)*V[it1];
			if(maxt>max)
				max=maxt;
			cout<<"本次操作的面积为："<<maxt<<endl;
			cout<<"累计操作的最大值为："<<max<<endl;
			if(V[it1+1]>V[it2-1])
				it1++;
			else if(V[it1+1]<=V[it2-1])
				it2--;
			//判断两侧的下一位谁大，谁大移动谁
			//对于下一位还相同的情况，则可以任选一侧，此处选的是右侧 
		}

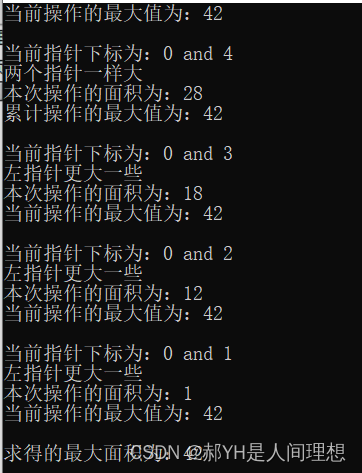
 结果与预期一致。