用C语言对学生成绩进行排序（归并排序与基数排序）

news2024/10/5 4:33:53

一.前言

我们内部排序已经学了插入排序（直接插入排序、折半插入排序、希尔排序），交换排序（冒泡排序、快速排序），选择排序（简单选择排序、堆排序），这些都属于内部排序，接下来我们学习内部排序里面剩下的归并排序和基数排序。

二.归并排序

1.算法思路

归并排序与上述基于交换、选择等排序的思想不一样，“归并”的含义是将两个或两个以上的有序表合并成一个新的有序表。假定待排序表含有n个记录，则可将其视为n个有序的子表，每个子表的长度为1,然后两两归并，得到[n/2]个长度为2或1的有序表;继续两两归并…如此重复，直到合并成-一个长度为n的有序表为止，这种排序方法称为2路归并排序。
分解:将含有n个元素的待排序表分成各含n/2个元素的子表，采用2路归并排序算法对两
个子表递归地进行排序。
合并:合并两个已排序的子表得到排序结果。

2.举例

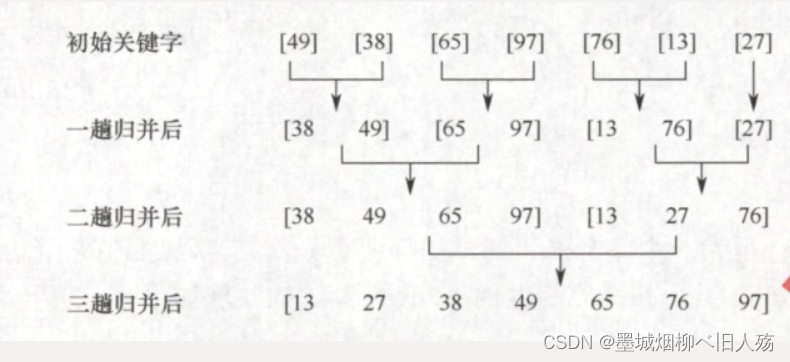
在这里插入图片描述

3.性能分析

  • 空间效率: Merge ()操作中，辅助空间刚好为n个早兀，所以算法的空间复朵度为O(n)。
  • 时间效率:每趟归并的时间复杂度为O(n)，共需进行[log2 n]趟归并，所以算法的时间复杂度为O(nlog2 n)。
  • 稳定性:由于Merge ()操作不会改变相同关键字记录的相对次序，所以2路归并排序算法是一种稳定的排序方法。

三.基数排序

1.算法思路

为实现多关键字排序，通常有两种方法:第-一种是最高位优先(MSD)法，按关键字位权重
递减依次逐层划分成若干更小的子序列，最后将所有子序列依次连接成-一个有序序列。第二种是最低位优先(LSD) 法，按关键字位权重递增依次进行排序，最后形成一个有序序列。

对i=0,d-1，依次做一-次“分配”和“收集”(其实是一次稳定的排序过程)。

  • 分配:开始时，把Qo, .,., Q-1各个队列置成空队列，然后依次考察线性表中的每个结点a; (j=0,1,.,n-1)， 若a;的关键字k;=k,就把a;放进Qk队列中。
  • 收集:把Qo, 0.,-, Qr1各个队列中的结点依次首尾相接，得到新的结点序列，从而组成新的线性表。

2.举例

通常采用链式基数排序，假设对如下10个记录进行排序:

在这里插入图片描述

依次取个位、十位、百位进行分配和收集：

在这里插入图片描述
每个关键字是1000 以下的正整数，基数r= 10，在排序过程中需要借助10个链队列，每个关键字由3位子关键字构成K’K2K’,分别代表百位、十位和个位，一共需要进行三趟“分配”和“收集”操作。第一趟分配用最低位子关键字K3进行，将所有最低位子关键字(个位)相等的记录分配到同一个队列，如图(a)所示，然后进行收集操作，第一趟收集后 的结果如图(b)所示。

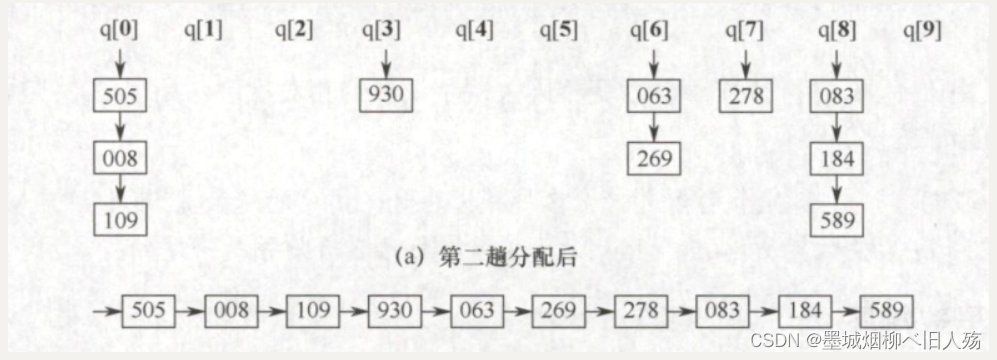
在这里插入图片描述
第二趟分配用次低位子关键字K2 进行，将所有次低位子关键字(十位)相等的记录分配到
同一个队列，如图(a)所示，第二趟收集后的结果如图(b)所示。

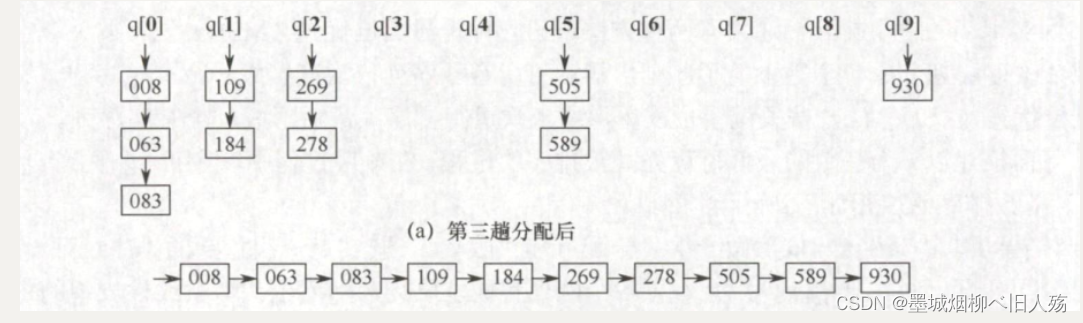
在这里插入图片描述
第三趟分配用最高位子关键字K’ 进行，将所有最高位子关键字(百位)相等的记录分配到
同一个队列，如图(a)所示，第三趟收集后的结果如图(b)所示，至此整个排序结束。

3.性能分析

  • 空间效率:一趟排序需要的辅助存储空间为r (r个队列: r个队头指针和r个队尾指针)，但以后的排序中会重复使用这些队列，所以基数排序的空间复杂度为0®。
  • 时间效率:基数排序需要进行d趟分配和收集，一趟分配需要O(n),一趟收集需要0®,所以基数排序的时间复杂度为O(d(n + r)),它与序列的初始状态无关。
  • 稳定性:对于基数排序算法而言，很重要一点就是按位排序时必须是稳定的。因此，这也保证了基数排序的稳定性。

四.排序算法代码

1.归并排序

Merge()的功能是将前后相邻的两个有序表归并为一个有序表。设两段有序表A[low.mid]、A[mid1…high]存放在同-顺序表中的相邻位置，先将它们复制到辅助数组B
中。每次从对应B中的两个段取出一一个 记录进行关键字的比较，将较小者放入A中，当数组B中有一段的下标超出其对应的表长(即该段的所有元素都已复制到A中)时，将另一段中的剩余部分直接复制到A中。算法如下:

//归并函数
Elemtype *A=(Elemtype *)malloc(MaxSize * sizeof(Elemtype));      //辅助数组
void Merge(SqList &L,int low,int mid,int high){     //这里三个指针不是为了快排，而是为了方便指示序列长度
	int i,j,k;
	for(k=low;k<=high;k++)
		A[k]=L.data[k];                                        //将L.data[]的所有元素复制到A中
	for(i=low,j=mid+1,k=i;i<=mid && j<=high;k++){
		if(A[i].grade<=A[j].grade)
			L.data[k]=A[i++];                       //比较左右两端元素的大小
		else
			L.data[k]=A[j++];
	}
	while(i<=mid)    L.data[k++]=A[i++];         //没检测完的直接复制
	while(j<=high)   L.data[k++]=A[j++];
}

//归并排序函数
void Mergesort(SqList &L,int low,int high){
	if(low<high){
		int mid=(low+high)/2;            //从中间划分两个子序列
		Mergesort(L,low,mid);           //对左侧子树进行递归排序
		Mergesort(L,mid+1,high);         //对右侧子树进行递归排序
		Merge(L,low,mid,high);          //归并
	}
}

2.基数排序

//基数排序
void Basesort(LinkNode &L, Saquene queue[]) {
	for (int radix = 1; radix <= 100; radix *= 10) { // 对每个位数进行排序
		// 入队列
		LinkNode p = L->next;
		while (p != NULL) {
			int i = (p->data.grade / radix) % 10;
			enQueue(queue[i], &(p->data));
			p = p->next;
		}
		// 出队列
		LinkNode tail = L;
		for (int i = 0; i < 10; i++) {
			while (!QueueEmpty(queue[i])) {
				Elemtype e;
				deQueue(queue[i], &e);
				LinkNode newNode = (LinkNode)malloc(sizeof(LNode));
				newNode->data = e;             //不断的“收集”
				newNode->next = NULL;
				tail->next = newNode;        //tail相当于一个头结点
				tail = newNode;
			}
		}
	}
}

五.完整C语言测试代码

1.测试归并排序

/*我们今天的主角是归并排序，所以我们还是利用线性表来进行模拟*/

/*为了便于我们后面演示希尔排序，所以我们采用顺序存储结构*/
#include <stdlib.h>
#include <stdio.h>
#include <string.h>

#define MaxSize 50                //这里只是演示，我们假设这里最多存五十个学生信息

//定义学生结构
typedef struct {
	char name[200];              //姓名
	int  grade;               //分数，这个是排序关键字
} Elemtype;

//声明使用顺序表
typedef struct {
	/*这里给数据分配内存，可以有静态和动态两种方式，这里采用动态分配*/
	Elemtype  *data;            //存放线性表中的元素是Elemtype所指代的学生结构体
	int length;                 //存放线性表的长度
} SqList;						//给这个顺序表起个名字，接下来给这个结构体定义方法

//初始化线性表
void InitList(SqList &L){
	/*动态分配内存的初始化*/
	L.data = (Elemtype*)malloc(MaxSize * sizeof(Elemtype));  //为顺序表分配空间
	L.length = 0;                                            //初始化长度为0
}

//求表长函数
int Length(SqList &L){
	return L.length;
}

//求某个数据元素值
bool GetElem(SqList &L, int i, Elemtype &e) {
	if (i < 1 || i > L.length)
		return false;         //参数i错误时，返回false
	e = L.data[i - 1];      //取元素值
	return true;
}

//输出线性表
void DispList(SqList &L) {
	if (L.length == 0)
		printf("线性表为空");
	//扫描顺序表，输出各元素
	for (int i = 0; i < L.length; i++) {
		printf("%s        %d", L.data[i].name,  L.data[i].grade);
		printf("\n");
	}
	printf("\n");
}

//插入数据元素
bool ListInsert(SqList &L, int i, Elemtype e) {
	/*在顺序表L的第i个位置上插入新元素e*/
	int j;
	//参数i不正确时，返回false
	if (i < 1 || i > L.length + 1 || L.length == MaxSize)
		return false;
	i--;                //将顺序表逻辑序号转化为物理序号
	//参数i正确时，将data[i]及后面的元素后移一个位置
	for (j = L.length; j > i; j--) {
		L.data[j] = L.data[j - 1];
	}
	L.data[i] = e;      //插入元素e
	L.length++;         //顺序表长度加1
	return true;
	/*平均时间复杂度为O(n)*/
}

//归并函数
Elemtype *A=(Elemtype *)malloc(MaxSize * sizeof(Elemtype));      //辅助数组
void Merge(SqList &L,int low,int mid,int high){     //这里三个指针不是为了快排，而是为了方便指示序列长度
	int i,j,k;
	for(k=low;k<=high;k++)
		A[k]=L.data[k];                                        //将L.data[]的所有元素复制到A中
	for(i=low,j=mid+1,k=i;i<=mid && j<=high;k++){
		if(A[i].grade<=A[j].grade)
			L.data[k]=A[i++];                       //比较左右两端元素的大小
		else
			L.data[k]=A[j++];
	}
	while(i<=mid)    L.data[k++]=A[i++];         //没检测完的直接复制
	while(j<=high)   L.data[k++]=A[j++];
}

//归并排序函数
void Mergesort(SqList &L,int low,int high){
	if(low<high){
		int mid=(low+high)/2;            //从中间划分两个子序列
		Mergesort(L,low,mid);           //对左侧子树进行递归排序
		Mergesort(L,mid+1,high);         //对右侧子树进行递归排序
		Merge(L,low,mid,high);          //归并
	}
}

int main(){
	SqList L;
	Elemtype stuents[10]={{"张三",649},{"李四",638},{"王五",665},{"赵六",697},{"冯七",676},
		{"读者",713},{"阿强",627},{"杨曦",649},{"老六",655},{"阿黄",604}};
	//这一部分忘了的请回顾我的相关博客
	printf("初始化顺序表并插入开始元素：\n");
	InitList(L);         //这时是一个空表，接下来通过插入元素函数完成初始化
	for (int i = 0; i < 10; i++)
		ListInsert(L, i + 1, stuents[i]);
	DispList(L);
	printf("根据分数进行归并排序后结果为:\n");
	int low=0,high=L.length-1;
	Mergesort(L,low,high);
	DispList(L);
}

2.测试基数排序

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#define MaxSize 50       //定义队列元素的最大个数
//定义学生结构
typedef struct {
	char name[20];              //姓名
	int  grade;               //分数
} Elemtype;

//声明链表
typedef struct LNode
{
	Elemtype data;
	struct LNode *next;
}LNode,*LinkNode;

//和上次实验的不同，上次实验初始化是建立一个头结点把next置为空
//这里用LinkNode L表示一个链表，用LNode *表示一个结点（该思路来源于王道考研）
//不带头结点链表的初始化
bool InitList1(LinkNode &L)
{
	L=NULL;
	return true;
}

//带头结点链表的初始化
bool InitList2(LinkNode &L){
	L=(LNode *)malloc(sizeof(LNode));
	if(L==NULL)
		return false;
	L->next=NULL;
	return true;
}

//尾插法建立单链表
void CreateListR(LinkNode &L,Elemtype a[],int n)
{
	LNode *s,*r;                      //r位始终指向尾结点的指针，而s为指向要插入结点的过度指针
	//头节点已存在，不再在这里建立了
	r=L;                       //r始终指向尾节点，但初始时指向头节点（初始时头节点即为尾节点）
	for(int i=0;i<n;i++)
	{
		s=(LNode * )malloc(sizeof(LNode));  //创建数据新节点
		s->data=a[i];                            //将数组元素赋值给新节点s的数据域
		r->next=s;                               //将s放在原来尾指针r的后面
		r=s;
	}
	r->next=NULL;                              //插入完成后，尾节点的next域为空
}

//头插法建立单链表
void CreateListF(LinkNode &L,Elemtype a[],int n)
{
	LNode *s;
	//头节点已存在，不再在这里建立了
	for(int i=0;i<n;i++)
	{
		s=(LNode * )malloc(sizeof(LNode));   //创建数据新节点
		s->data=a[i];                              //将数组元素赋值给s的数据域
		s->next=L->next;                          //将s放在原来L节点之后
		L->next=s;
	}
}
/*头插法和尾插法一定要画图弄清思路*/

//按序号查找结点
LNode *GetElem(LinkNode &L,int i){
	if(i<1)
		return NULL;
	int j=1;
	LNode *p=L->next;
	while(p!=NULL && j<i){
		p=p->next;
		j++;
	}
	return p;
}

//插入数据元素
bool ListInsert(LinkNode &L,int i,Elemtype e)
{
	/*在链表L的第i个位置上插入新元素e*/
	int j=0;
	LNode *p=L,*s;      //p开始指向头节点，s为存放数据新节点
	if(i<=0)               //位置不对就报错
		return false;
	while(j<i-1 && p!=NULL)       //定位，使p指向第i-1个节点
	{
		j++;
		p=p->next;
	}
	if(p==NULL)                 //如果没找到第i-1个节点就报错
		return false;
	else                        //成功定位后，执行下面操作
	{
		s=(LNode * )malloc(sizeof(LNode));          //创建新节点s，其数据域置为e
		s->data=e;
		s->next=p->next;                                //创建的新节点s放在节点p之后
		p->next=s;
		return true;
	}
}

//输出线性表
void DispList(LinkNode &L)
{
	LinkNode p=L->next;                   //p指向首节点
	while(p!=NULL)                         //p不为空就输出p节点的data域
	{
		printf("%s        %d\n",p->data.name,p->data.grade);
		p=p->next;	                       //p移向下一位节点
	}
	printf("-------------------------------\n");
}

//定义循环顺序队列结构体
typedef struct {
	Elemtype data[MaxSize]; //存放队中元素
	int front, rear; //队头和队尾的伪指针
} SqQueue, *Saquene; //顺序队类型

//初始化队列
void InitQueue(Saquene *q) {
	*q = (SqQueue *) malloc(sizeof(SqQueue)); //申请一个顺序队大小的空队列空间
	(*q)->front = (*q)->rear = 0; //队头和队尾的伪指针均设置伪-1
}

//销毁队列
void DestroyQueue(Saquene q) {
	free(q); //释放q所占的空间即可
}

//判断空队列
int QueueEmpty(Saquene q) {
	return (q->front == q->rear);
}

//进队列
int enQueue(Saquene q, Elemtype *e) {
	if ((q->rear + 1) % MaxSize == q->front) //队满上溢出报错
		return 0;
	q->rear = (q->rear + 1) % MaxSize; //队尾增1
	q->data[q->rear] = *e; //rear位置插入元素e
	return 1;
}

//出队列
int deQueue(Saquene q, Elemtype *e) {
	if (q->rear == q->front) //队空下溢出报错
		return 0;
	q->front = (q->front + 1) % MaxSize; //队头增1
	*e = q->data[q->front];
	return 1;
}

//基数排序
void Basesort(LinkNode &L, Saquene queue[]) {
	for (int radix = 1; radix <= 100; radix *= 10) { // 对每个位数进行排序
		// 入队列
		LinkNode p = L->next;
		while (p != NULL) {
			int i = (p->data.grade / radix) % 10;
			enQueue(queue[i], &(p->data));
			p = p->next;
		}
		// 出队列
		LinkNode tail = L;
		for (int i = 0; i < 10; i++) {
			while (!QueueEmpty(queue[i])) {
				Elemtype e;
				deQueue(queue[i], &e);
				LinkNode newNode = (LinkNode)malloc(sizeof(LNode));
				newNode->data = e;             //不断的“收集”
				newNode->next = NULL;
				tail->next = newNode;        //tail相当于一个头结点
				tail = newNode;
			}
		}
	}
}
/*这里容易产生一个思维误区，由于我们这里是链表，它是一个一个结点构成的，在我们进队操作时，原来的链表相当于被我们打散了
  分成一个个结点插入不同的队列中，在后面收集的出队过程中，我们又把每个结点拿出来重新链接，所以最后结果就相当于在原来的线性表L上修改*/
int main(){
	LinkNode L;
	Elemtype stuents[10]={{"张三",649},{"李四",638},{"王五",665},{"赵六",697},{"冯七",676},
		{"读者",713},{"阿强",627},{"杨曦",649},{"老六",655},{"阿黄",604}};
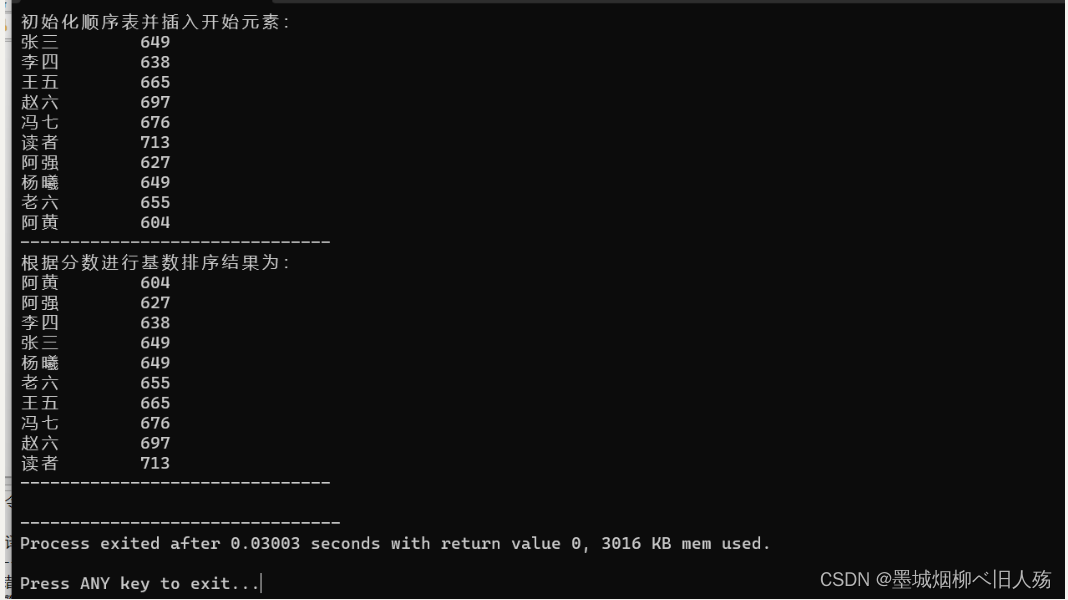
	printf("初始化顺序表并插入开始元素：\n");
	InitList2(L);         //这时是一个空表，接下来通过插入元素函数完成初始化
	for (int i = 0; i < 10; i++)
		ListInsert(L, i + 1, stuents[i]);
	DispList(L);
	//这一步是验证了插入函数是正确的，我们通过for循环插入
	//同时，我还写了头插法和尾插法建立单链表，可以直接使用这两个算法建立单链表，把students[]作为参数传入即可
	Saquene queue[10];            //定义十个队列
	for(int i=0;i<10;i++){
		Saquene a;
		InitQueue(&a);
		queue[i]=a;
	}
	
	Basesort(L, queue); // 基数排序
	DispList(L); // 输出排序后的链表
	
	return 0;
	
}

六.测试结果

1.归并排序测试结果

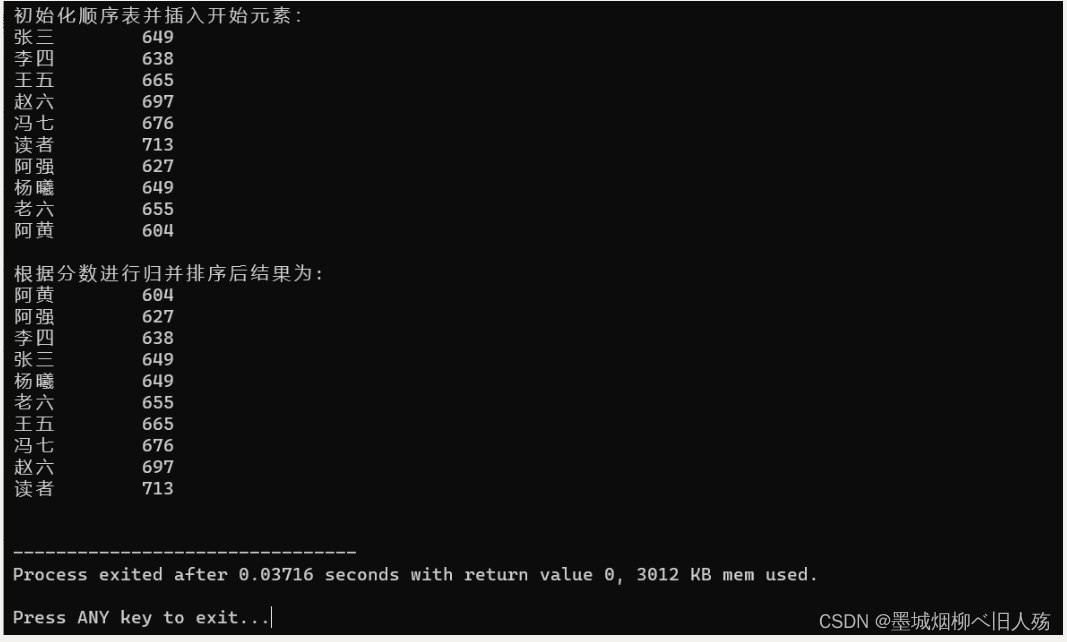
在这里插入图片描述

2.基数排序测试结果

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/769228.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ShardingSphere分库分表实战之绑定表

ShardingSphere分库分表实战之绑定表

&#x1f680; ShardingSphere &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&…
阅读更多...
DAY48：动态规划（十二）完全平方数（类似零钱兑换）+单词拆分（注意背包思路！）

DAY48：动态规划（十二）完全平方数（类似零钱兑换）+单词拆分（注意背包思路！）

文章目录 279.完全平方数&#xff08;类似零钱兑换&#xff09;思路DP数组含义递推公式初始化遍历顺序 最开始的写法&#xff1a;有1个用例没过修改完整版总结 139.单词拆分&#xff08;递推公式注意&#xff09;思路1&#xff1a;遍历单词分割点DP数组含义递推公式初始化遍历顺…
阅读更多...
基于Java+SpringBoot+Vue前后端分离旅游网站详细设计和实现

基于Java+SpringBoot+Vue前后端分离旅游网站详细设计和实现

博主介绍&#xff1a;✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ &#x1f345;文末获取源码联系&#x1f345; &#x1f447;&#x1f3fb; 精彩专…
阅读更多...
导航菜单 改变背景色

导航菜单 改变背景色

直接参考官网上的案例即可 //active-text-color 点击时修改字体颜色 // background-color 背景色 // text-color 字体颜色<el-menudefault-active"2"class"el-menu-vertical-demo"open"handleOpen"close"handleClose"background…
阅读更多...
Java：控制流程 + 数组 详解（原理 + 用法 + 例子）

Java：控制流程 + 数组 详解（原理 + 用法 + 例子）

目录 控制流程块作用域if 条件语句for while 循环switch 多重选择break continue 中断控制流程语句 大数值数组多维数组字符串类型数组Array.sort() 数组排序for each 循环 控制流程 块作用域 块&#xff08;即复合语句&#xff09;是指由一对大括号{}括起来的若干条简单的 Ja…
阅读更多...
ARP解析MAC地址的全过程（ARP的工作机制）

ARP解析MAC地址的全过程（ARP的工作机制）

目录 ARP解析MAC地址的过程&#xff1a; 源码等资料获取方法 以太网环境下&#xff0c;同一个网段的主机之间需要互相知道对方的MAC地址&#xff0c;才能访问。 TCP/IP协议栈从上层到下层的封装过程中&#xff0c;第三层封装需要知道目的IP&#xff0c;第二层封装需要知道目…
阅读更多...
Linux下安装Mysql (CentOS 7) 详解

Linux下安装Mysql (CentOS 7) 详解

文章目录 前言环境检查查看是否安装MySql查看系统版本 源安装安装mysql的yum源官网下载从windows上传到linuxrz命令 方法2&#xff1a; 安装Mysql常见错误密钥问题安装后查看mysql是否可以工作查看是否安装成功启动服务 登录mysql配置文件方法&#xff08;免密码&#xff09; 使…
阅读更多...
linux 安装 cuda

linux 安装 cuda

需求&#xff1a; inux 下安装 cuda 进程&#xff1a; 先查看一下系统版本 uname -a查看能支持什么版本的cudacuda toolkit 下载 wget https://developer.download.nvidia.com/compute/cuda/11.1.0/local_installers/cuda_11.1.0_455.23.05_linux.run sudo sh cuda_11.1.0_4…
阅读更多...
MySql冷门但是很有用的语句

MySql冷门但是很有用的语句

目录 1 查看当前的所有执行的进程 查看简略信息 查看详细信息 2 在所有数据库中查询包含某个字段的表 精确 模糊 1 查看当前的所有执行的进程 查看简略信息 show processlist 查看详细信息 show full processlist 终止进程 kill id 2 在所有数据库中查询包含某个字段…
阅读更多...
gurobi安装vs配置gurobi

gurobi安装vs配置gurobi

gurobi安装&vs配置gurobi 1、注册账号并登录 2、下载gurobi optimizer 3、获取license:User Portal (gurobi.com) online course可以免ip验证。 4、GENERATE NOW会生成&#xff0c;打开cmd进入gurobi安装路径&#xff08;如F:\gurobi1001\win64\bin>&#xff09;&am…
阅读更多...
分布式事务 Seata

分布式事务 Seata

分布式事务 Seata 事务介绍分布式理论Seata 介绍Seata 部署与集成Seata TC Server 部署微服务集成 Seata XA 模式AT 模式AT 模式执行过程读写隔离写隔离读隔离 实现 AT 模式 TCC 模式TCC 模式介绍实现 TCC 模式 Saga 模式Seata 四种模式对比 事务介绍 事务&#xff08;Transac…
阅读更多...
分布式光伏监控系统运维系统实时查看数据分布式光伏电站监控管理

分布式光伏监控系统运维系统实时查看数据分布式光伏电站监控管理

光伏电站是一种利用太阳能发电的设施&#xff0c;随着人们对可再生能源的需求不断增加&#xff0c;光伏电站的建设也越来越普遍。但是&#xff0c;光伏电站的运营和管理需要高质量的监控系统来确保其正常运行。本文将介绍光伏电站监控系统的组成及其原理。 详细软件具体需求可…
阅读更多...
php连接上mysql数据库该的配置方法

php连接上mysql数据库该的配置方法

用mysql官方的管理工具workbench&#xff1a; 打开导出界面后&#xff0c;下一步&#xff0c;选择csv格式&#xff0c;导出后excel就能打开了 如果你需要在程序代码中导出&#xff0c;需要找到对应代码的excel处理库。 如php 的 phpExcel( 最新版已更名为 phpoffice/phpspread…
阅读更多...
vue3组件中使用live2d看板娘（官方包形式）

vue3组件中使用live2d看板娘（官方包形式）

文章目录 先看最终效果吧关于官方包下载使用 vue3中调整使用基础使用关于样式调整 vue中Html主页调试&#xff08;备用调试方案&#xff09; 先看最终效果吧 看着还可以&#xff0c;其实还有很多问题没解决&#xff0c;因为是完全靠js渲染&#xff0c;实际上这个live2d的canvas…
阅读更多...
前端开发多人协作的团队项目时应该要配置的一些规则

前端开发多人协作的团队项目时应该要配置的一些规则

本文主要记录了团队开发一个前端项目需要进行的一些前期配置&#xff0c;例如Eslint语法检验&#xff0c;prettierrc格式化规则&#xff0c;以及提交代码时的规则等等。 目录 1.搭建项目 2.Eslint配置&#xff08;代码检验工具&#xff09; 2.1安装Eslint 2.2配置Eslint 2…
阅读更多...
【Ajax】笔记-取消请求

【Ajax】笔记-取消请求

在进行AJAX(Asynchronous JavaScript and XML) 请求时&#xff0c;有时候我们需要取消正在进行的请求。取消请求可以帮助我们提高用户体验&#xff0c;病减少不必要的网络流量和服务器负载。 取消请求的方法 在AJAX请求中&#xff0c;我们可以使用以下方法来取消正在进行的请求…
阅读更多...
【大虾送书第三期】进阶高级Python开发工程师，不得不掌握的Python高并发编程

【大虾送书第三期】进阶高级Python开发工程师，不得不掌握的Python高并发编程

目录 ✨写在前面 ✨主要内容 ✨本书特色 ✨关于作者 &#x1f990;博客主页&#xff1a;大虾好吃吗的博客 &#x1f990;专栏地址&#xff1a;免费送书活动专栏地址 写在前面 Python成为时下技术革新的弄潮儿&#xff0c;全民Python的发展趋势让人们不再满足于简单地运行Python…
阅读更多...
MacBook Java开发环境搭建记录

MacBook Java开发环境搭建记录

一、Homebrew的镜像设置 对于Java JDK的安装&#xff0c;我们更推荐使用Homebrew来进行安装管理。但Homebrew的curl国外源的下载速度实在是一言难尽&#xff0c;时常还会发生无法访问的情况。 那么我们此时的解决方法就有两种了&#xff0c;第一种便是使用全局的VPN代理进行下载…
阅读更多...
SQLite Expert Personal的简单使用

SQLite Expert Personal的简单使用

官方网站&#xff1a; sqliteexpert官方网址 - SQLite administration | SQLite Expert ​—————————————————————————————————————————— 免费的受欢迎的 SQLite 管理工具 SQLite Manager 0.8.0 Firefox Plugin 这是一个 Firefox …
阅读更多...
【MySQL】多表查询(四)

【MySQL】多表查询(四)

&#x1f697;MySQL学习第四站~ &#x1f6a9;本文已收录至专栏&#xff1a;MySQL通关路 ❤️文末附全文思维导图&#xff0c;感谢各位点赞收藏支持~ 之前我们介绍DQL语句&#xff0c;也就是数据查询语句的时候&#xff0c;介绍的查询操作都是单表查询&#xff0c;他的功能当然…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023