$Wasserstein$ $distance$一般被称为推土距离，假设有两个分布$P(x)$和$Q(y)$ ，两个分布间的推土距离为：$$W(P,Q)=\underset{\gamma \in \Pi (P,Q)}{\inf }{\mathbb{E}}_{(x,y)}[\Vert x-y\Vert ]$$公式中的$\Pi (P,Q)$表示$P$和$Q$的联合概率分布的集合，$\Vert x-y\Vert$表示待移动土块$x$所在位置到目的土块$y$所在位置的距离（距离的计算方式有很多种），$inf$表示求最小值。

第一次看这个公式的时候，有个疑问是既然给定$P$和$Q$之后，$P$和$Q$之间的概率分布不是确定了吗？为什么还会存在$P$和$Q$的概率分布集合？

在概率论中，如果我们有两个随机变量$X$和$Y$，它们的联合概率分布是确定的，因为它描述了$X$和$Y$同时发生的概率。然而，在$Wasserstein$距离的计算中，我们并不是在讨论两个随机变量的联合概率分布，而是在寻找一个联合概率分布，使得它的边缘分布分别等于给定的两个概率分布$P$和$Q$，并且使得某种成本（例如，所有可能的配对之间的距离的期望值）最小。

这个问题被称为最优传输问题或者Earth Mover’s Distance问题。在这个问题中，我们可以想象$P$和$Q$分别代表了两堆土，我们的目标是找到一种最经济的方式，将$P$堆的土移动到$Q$堆的位置。在这个过程中，我们可以有无数种可能的移动策略，每种策略都对应了一个联合概率分布，这个联合概率分布描述了从$P$堆的每个位置到$Q$堆的每个位置的移动概率。我们的目标是找到一种移动策略，使得移动的总成本最小，这就是为什么在$Wasserstein$距离中，我们需要在所有可能的联合概率分布中寻找最优的那一个。

看了上面，可能还是不懂，联合概率分布是怎么对应一个移动策略的？下面通过一个简单例子来说明一下联合概率分布怎么对应移动策略。

假定$Q$分布和$P$分布如下所示：

现在演示将$P$移动成$Q$的一种方法，并使用一个表格记录移动过程：

• 第一步：移动$y_1$，如下所示：
  对应的表格记录为：

  搬运过程			Q
  			x1	x2	x3	x4	x5
  			2	3	4	5	0
  P	y1	3	2	1	0	0	0
  	y2	5	0	0	0	0	0
  	y3	2	0	0	0	0	0
  	y4	1	0	0	0	0	0
  	y5	3	0	0	0	0	0

  表格的意思是将$P$中$y_1$ 的两份土搬运到$x_1$，将$y_1$的一份土搬运到$x_2$，这时候$y_1$的土搬运完毕；

• 第二步：移动$y_2$，如下所示：
  
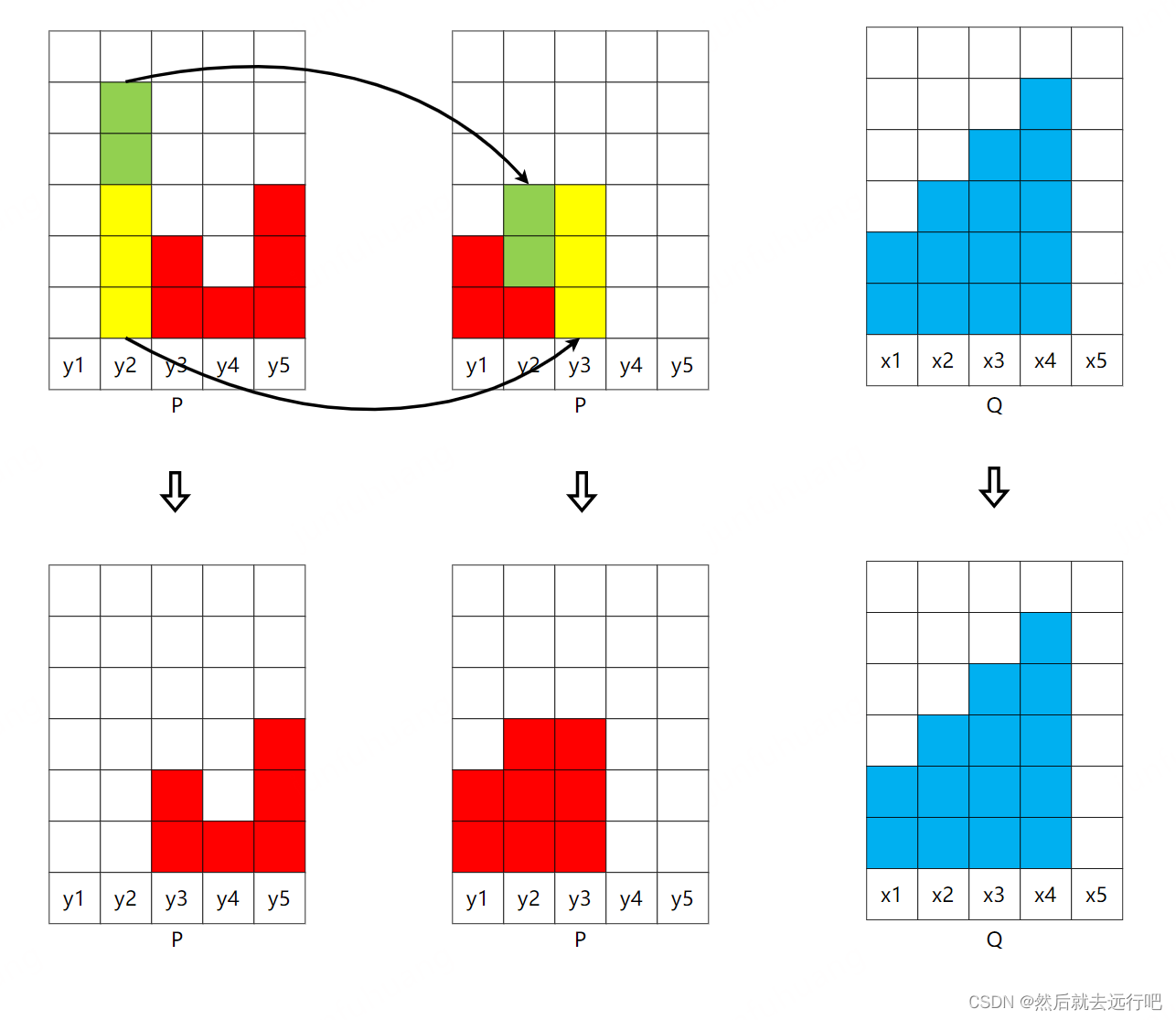
  对应的表格记录为：

  搬运过程			Q
  			x1	x2	x3	x4	x5
  			2	3	4	5	0
  P	y1	3	2	1	0	0	0
  	y2	5	0	2	3	0	0
  	y3	2	0	0	0	0	0
  	y4	1	0	0	0	0	0
  	y5	3	0	0	0	0	0

  表格的意思是将$P$中$y_2$ 的两份土搬运到$x_2$，将$y_2$的三份土搬运到$x_3$，这时候$y_2$的土搬运完毕；

• 第三步：移动$y_3$，如下所示：
  
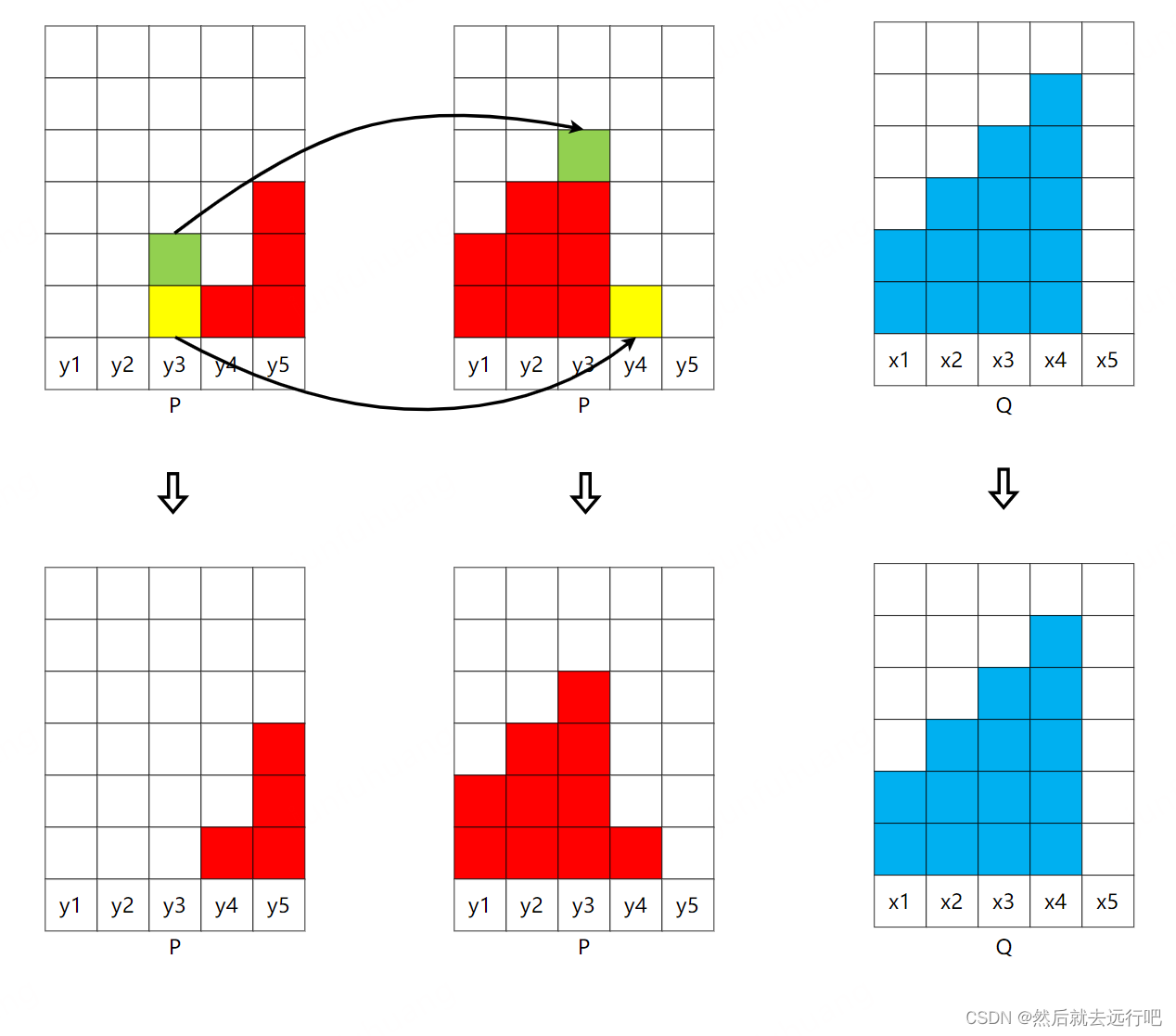
  对应的表格记录为：

  搬运过程			Q
  			x1	x2	x3	x4	x5
  			2	3	4	5	0
  P	y1	3	2	1	0	0	0
  	y2	5	0	2	3	0	0
  	y3	2	0	0	1	1	0
  	y4	1	0	0	0	0	0
  	y5	3	0	0	0	0	0

  表格的意思是将$P$中$y_3$ 的一份土搬运到$x_3$，将$y_3$的一份土搬运到$x_4$，这时候$y_3$的土搬运完毕；

• 第四步：移动$y_4$，如下所示：
  
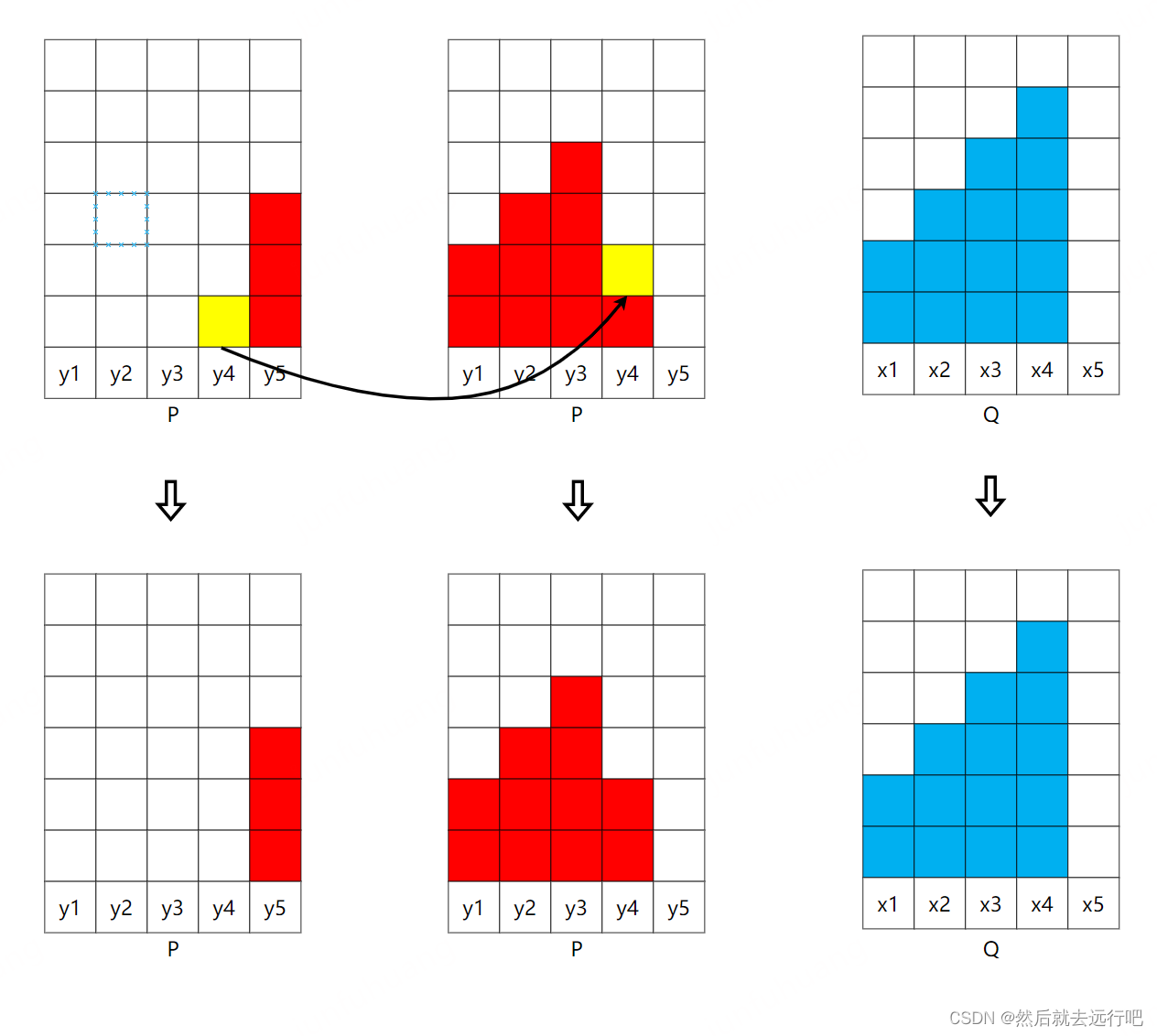
  对应的表格记录为：

  搬运过程			Q
  			x1	x2	x3	x4	x5
  			2	3	4	5	0
  P	y1	3	2	1	0	0	0
  	y2	5	0	2	3	0	0
  	y3	2	0	0	1	1	0
  	y4	1	0	0	0	1	0
  	y5	3	0	0	0	0	0

  表格的意思是将$P$中$y_4$的一份土搬运到$x_4$，这时候$y_4$的土搬运完毕；

• 第五步：移动$y_5$，如下所示：
  
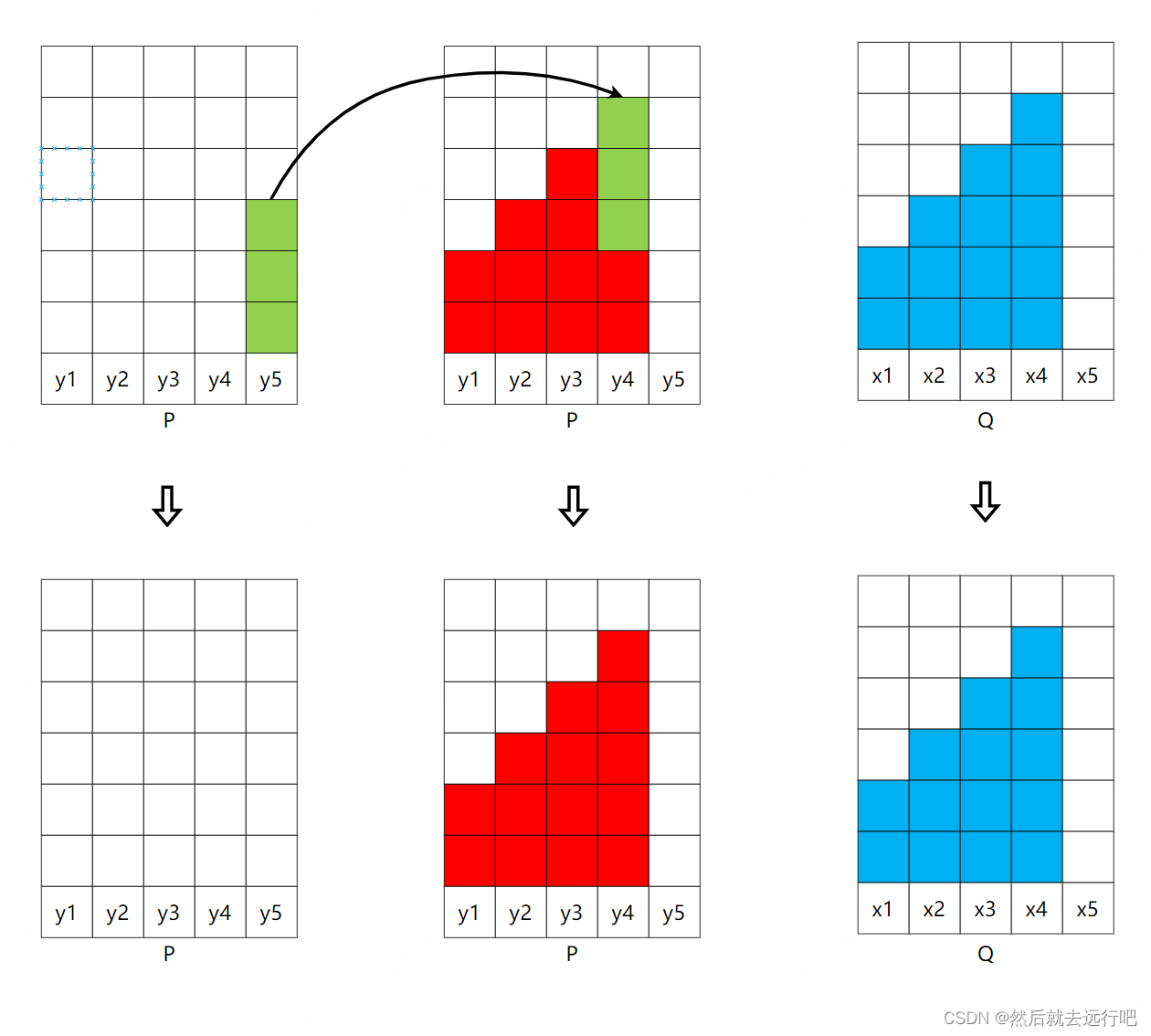
  对应的表格记录为：

  搬运过程			Q
  			x1	x2	x3	x4	x5
  			2	3	4	5	0
  P	y1	3	2	1	0	0	0
  	y2	5	0	2	3	0	0
  	y3	2	0	0	1	1	0
  	y4	1	0	0	0	1	0
  	y5	3	0	0	0	3	0

  表格的意思是将$P$中$y_5$的三份土搬运到$x_4$，这时候$y_5$的土搬运完毕；

通过上面的例子，我们知道了将$P$搬运成$Q$的一种策略，那么这种策略怎么和联合概率分布联系起来呢？注意我们在搬运过程中得到了一个表格。如下所示：

搬运过程			Q
			x1	x2	x3	x4	x5
			2	3	4	5	0
P	y1	3	2	1	0	0	0
	y2	5	0	2	3	0	0
	y3	2	0	0	1	1	0
	y4	1	0	0	0	1	0
	y5	3	0	0	0	3	0

在搬运过程中$P$中所有土的数量为$$3+5+2+1+3=14$$我们将14作为分母放进表格中可以得到：

搬运过程			Q
			x1	x2	x3	x4	x5
			2	3	4	5	0
P	y1	3	2/14	1/14	0	0	0
	y2	5	0	2/14	3/14	0	0
	y3	2	0	0	1/14	1/14	0
	y4	1	0	0	0	1/14	0
	y5	3	0	0	0	3/14	0

现在在回过头来看这个表格，是不是看着和联合概率分布很像了。所以说一种移动策略对应一种联合概率分布，我们需要得到的是使得距离之和最小的一个概率分布。我们可以有很多种移动策略，对应于公式中的联合概率分布集合$\Pi (P,Q)$，我们需要做的是在这么多种联合概率分布中找到一个最符合条件的，在$Wasserstein$距离中就是使得距离之和最小的联合概率分布。

所以我们可以理解$Wasserstein$距离为求解带约束的最优化问题，我们可以通过数学方法来求解得到最优的联合概率分布值。

这是我暂时对于$Wasserstein$距离的理解，如果有错误很抱歉。

参考资料：还看不懂Wasserstein Distance吗？看看这篇。