流体力学中动力粘度和运动粘度的定义和相互关系
在流体力学中,常遇到动力粘度和运动粘度参数。本文讲解这两个参数的含义和相关关系。
1.动力粘度(Dynamic viscosity)
1.1 动力粘度定义
动力粘度(dynamic viscosity),也被称为动态粘度、绝对粘度或简单粘度,定义为应力与应变速率之比,其数值上等于面积为1㎡相距1m的两平板,以1m/s的速度作相对运动时,因之间存在的流体互相作用所产生的内摩擦力。用它以表征流体粘性的内摩擦系数,用μ表示,如图1所示。
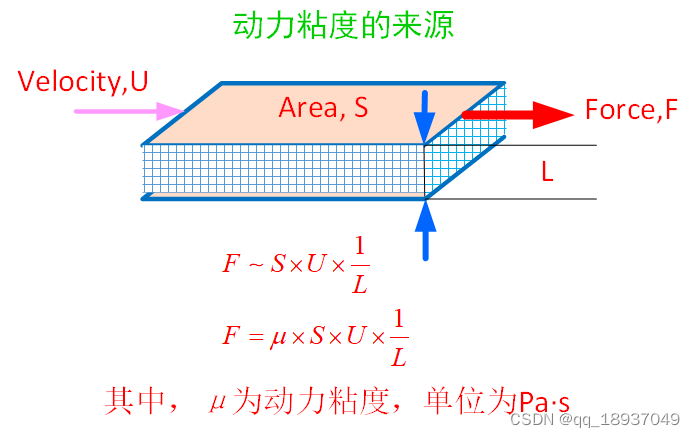
图1 动力粘度的来源
1.2 动力粘度的单位
动力粘度(希腊字母 μ \mu μ)的国际单位制是 P a ⋅ s Pa\cdot s Pa⋅s,它与 k g m ⋅ s \frac{kg}{m\cdot s} m⋅skg等同。
1.3 动力粘度和运动粘度的关系
动力粘度(dynamic viscosity)与运动粘度( kinematic viscosity)的关系为:
μ
=
ρ
⋅
ν
\mu=\rho\cdot\nu
μ=ρ⋅ν
其中,
ρ
\rho
ρ是密度,
ν
\nu
ν是运动粘度。
1.4 动力粘度的表达方式
在计算流体动力学使用中,动力粘度通过不同表达定义:
- 作为一个常数
- 作为温度的函数(例如,通过Sutherland定律或幂律粘度定律作为分段线性,分段多项式,多项式)
- 使用动力理论
- 成分相关
- 通过非牛顿模型
2.运动粘度(kinematic viscosity)
运动粘度
ν
\nu
ν被定义为:
ν
≡
μ
ρ
\nu \equiv \frac{\mu}{\rho}
ν≡ρμ
其中,
μ
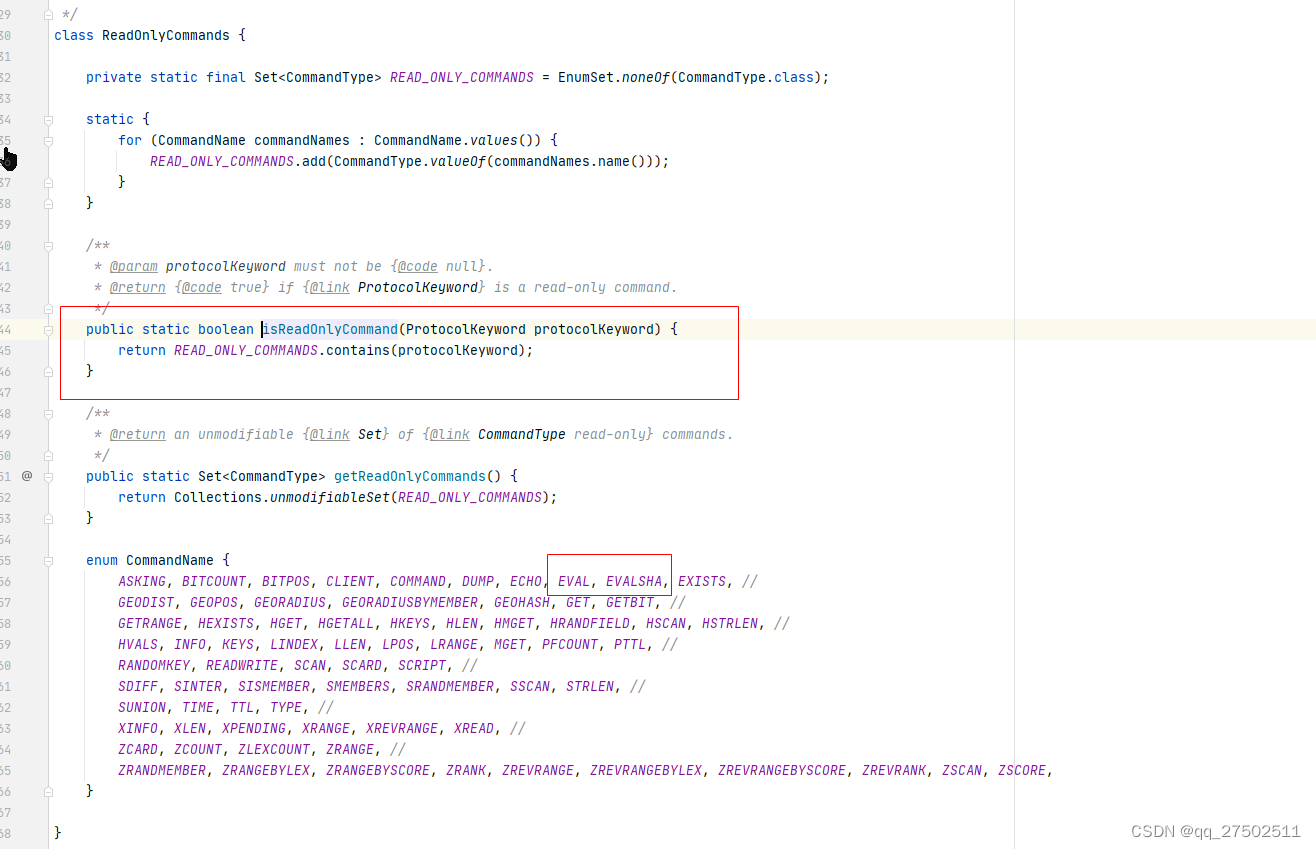
\mu
μ是动力粘度,
ρ
\rho
ρ是密度。运动粘度的国际单位制为
m
2
s
\frac{m^2}{s}
sm2