#! https://zhuanlan.zhihu.com/p/644157062
【method】ADMM-CSNet | 一种图像压缩感知重建的深度学习方法(1)- 方法解析

文章目录
- 【method】ADMM-CSNet | 一种图像压缩感知重建的深度学习方法(1)- 方法解析
- 摘要
- 广义压缩感知模型
- 1.Model
- 2. ADMM Solver
- 3.重建的高效计算
- 用于CS成像的ADMM-CSNET
- 1.Basic-ADMM-CSNet
- 2. Generic-ADMM-CSNet
- 3. Network Structure Analysis
- 网络训练
- 参考资料
🎯 Paper: https://ieeexplore.ieee.org/document/8550778
🚀 matlab: https://github.com/yangyan92/Deep-ADMM-Net
🚀pytorch: https://github1s.com/lixing0810/Pytorch_ADMM-CSNet/blob/HEAD/network/CSNet_Layers.py
摘要
本文将传统的基于模型的CS方法和数据驱动的深度学习方法相结合,地考虑了一个图像重建的广义CS模型,使用ADMM算法求解该模型,并进一步将ADMM算法扩展为unrolling深度网络,使得ADMM的所有参数通过端到端判别学习实现。
该方法在复数MR成像和实自然图像上实现了较好的重建精度。
广义压缩感知模型
本节展示了generalized CS model并提出了两种ADMM迭代求解方法。
1.Model
有约束的标准CS模型定义为:

- 稀疏系数 s s s目标使用正交稀疏基 Ψ \Psi Ψ重构原始信号 x x x,即 x = Ψ s x = \Psi s x=Ψs;
- y y y为 x x x的观测, Φ \Phi Φ为随机欠采样矩阵;

Ψ l + \Psi_l^+ Ψl+是 Ψ + 的第 \Psi^+的第 Ψ+的第 l l l行。
由于 x x x任意分辨率,进一步将图像表示 Ψ + x \Psi^+ x Ψ+x推广到使用固定局部滤波器的图像卷积,并将 l 1 l_1 l1正则推广到更通用的正则化 g ( ⋅ ) g(\cdot) g(⋅)。这便可以放松对 Ψ \Psi Ψ正交性和可逆性的要求,定义广义CS模型:

D l D_l Dl为第 l l l个卷积运算的变换矩阵, l l l为滤波器的数量。
说明:特殊情况下,举个例子
D
l
D_l
Dl可以是离散余弦变换,
g
(
⋅
)
g(\cdot)
g(⋅)可以为
l
q
,
q
∈
[
0
,
1
]
l_q,q\in[0,1]
lq,q∈[0,1]稀疏正则。在本文中把他们设置为可学习的。
2. ADMM Solver
下面根据引入辅助变量方式的不同,提出了两种ADMM求解器:
a. Solver 1:引入变换域独立辅助变量 z = z 1 , . . . , z L z = {z_1,...,z_L} z=z1,...,zL,则公示(8)等价于

其增广拉格朗日函数形式为

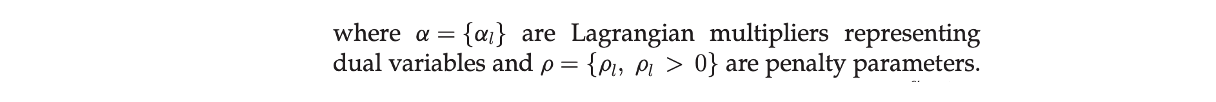
< α l , D l x − z l > = α l ( D l x − z l ) <\alpha_l,D_lx-z_l> = \alpha_l(D_lx-z_l) <αl,Dlx−zl>=αl(Dlx−zl); λ , ρ \lambda,\rho λ,ρ为人为设定的惩罚因子。
接着令 β l = α l ρ l \beta_l = \frac{\alpha_l}{\rho_l} βl=ρlαl,则ADMM可以用简化版缩放形式替代,通过交替优化下面的子问题求解:

η l \eta_l ηl为拉格朗日乘数的更新率
上述ADMM缩放形式推导:(具体推导参考自【1】【凸优化笔记7】-交替方向乘子法(ADMM) - 知乎 (zhihu.com))
ADMM solver[11]可以通过下面的迭代式进行求解:

n n n代表有多少次迭代, H H H为共轭转置, S ( ⋅ ) S(\cdot) S(⋅)表示具有参数 λ l / ρ l \lambda_l/\rho_l λl/ρl的关于 g ( ⋅ ) g(\cdot) g(⋅)的非线性近端映射(参考【2】近端映射与软阈值)算子,通常是软阈值或者硬阈值函数,分别对应 l 1 l_1 l1或者 l 0 l_0 l0稀疏正则化,具体可以看参考【2】。
上述求解式的推导如下:(参考【1】)
b. Solver 2:在图像域中引入辅助变量 z z z,则公示(8)等价于:

增广拉格朗日函数为:
令 β l = α l ρ l \beta_l = \frac{\alpha_l}{\rho_l} βl=ρlαl,则ADMM缩放形式为:

[15] 可以通过下面的迭代式进行求解:

一种求解[15]中第二项的方法是直接进行梯度下降,如[17],其中 H ( ⋅ ) H(\cdot) H(⋅)表示正则项 g ( ⋅ ) g(\cdot) g(⋅)的导数。

3.重建的高效计算
略
用于CS成像的ADMM-CSNET
1.Basic-ADMM-CSNet
基于ADMM solver I (公式[12]),如图[1]:

2. Generic-ADMM-CSNet
对solver2使用神经网络进行拓展,提出Generic-ADMM-CSNet。
下图为提出的网络结构:
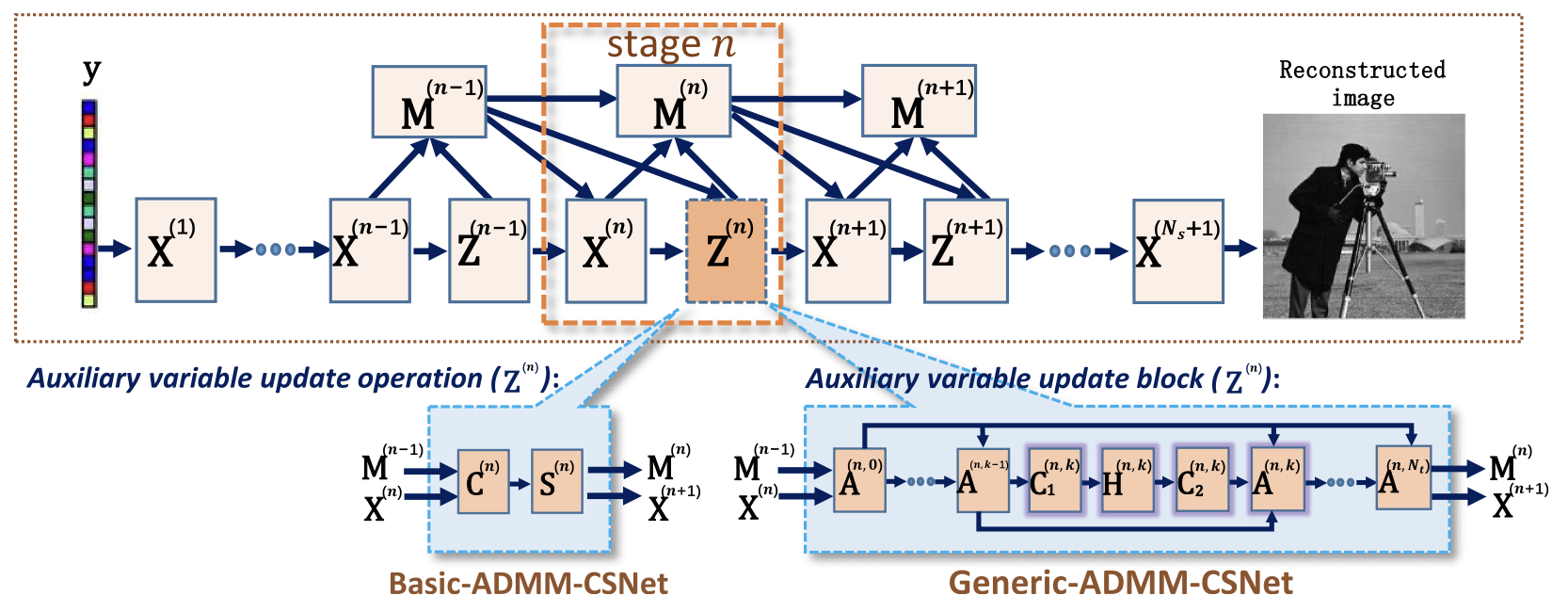

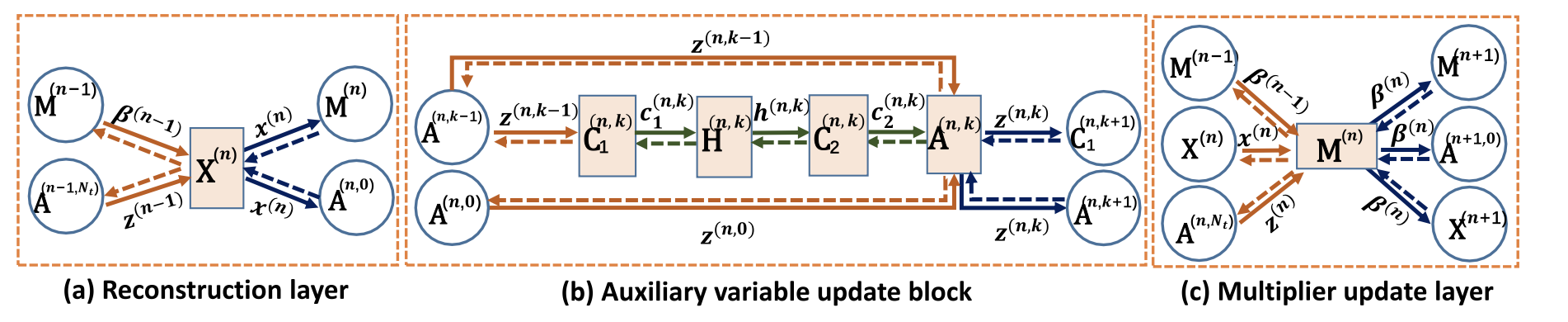
图二 data flow:实心箭头表示正向过程中的数据流,虚线箭头表示反向传播中的反向流。
整个迭代流程为: (除了整个结构的迭代循环,z zz 的内部(红色框部分)又有多次的迭代循环)

**a. Reconstruction Layer X ( n ) X^{(n)} X(n):**并没有约束不同阶段的网络结构要相同;每个阶段的输出为

在第一阶段,定义
**b.Multiplier Update Layer M ( n ) M^{(n)} M(n):**模块的输出为

c.Auxiliary Variable Update Block
auxiliary variable update block to implement Z ( n ) \mathbf{Z}^{(n)} Z(n) in eqn. [16],参考公式[17]对 Z ( n ) \mathbf{Z}^{(n)} Z(n)进行求解。

每个auxiliary variable update block包括:两个卷积层 ( C 1 ( n , k ) , C 2 ( n , k ) ) (\mathbf{C}_1^{(n,k)},\mathbf{C}_2^{(n,k)}) (C1(n,k),C2(n,k)),一个非线性激活层 H \mathbf{H} H,和一个addition layer A \mathbf A A。其中n表示第n和block,k表示迭代次数
-
卷积层 ( C 1 ( n , k ) , C 2 ( n , k ) ) (\mathbf{C}_1^{(n,k)},\mathbf{C}_2^{(n,k)}) (C1(n,k),C2(n,k)),分别代表 D l , D l T D_l,D_l^T Dl,DlT。
-
非线性激活层 H ( n , k ) \mathbf{H}^{(n,k)} H(n,k):我们不将其定义为公式8中的正则 g ( ) g() g()的导数,而是使用分段线性函数去学习一个广义的函数,如下,公式3举了例子:
 注意:当
c
1
(
n
,
k
)
c_1^{(n,k)}
c1(n,k)为复数,我们需要对实部和虚部分开求解,并且实部和虚部共享分段线性函数,如下:
注意:当
c
1
(
n
,
k
)
c_1^{(n,k)}
c1(n,k)为复数,我们需要对实部和虚部分开求解,并且实部和虚部共享分段线性函数,如下:
-
Addition Layer A ( n , k ) \mathbf A^{(n,k)} A(n,k):简单的加权算子,定义初始化为 A ( n , 0 ) : z ( n , 0 ) = x ( n ) + β ( n − 1 ) \mathbf A^{(n,0)}: z^{(n,0)} = x^{(n)}+\beta^{(n-1)} A(n,0):z(n,0)=x(n)+β(n−1)。该模块的输出为:

因此,the output of the auxiliary variable update block in n n n-th stage is z ( n ) = z ( n , N − t ) z^{(n)} = z^{(n,N-t)} z(n)=z(n,N−t) 。
模型的可学习参数分析:

3. Network Structure Analysis
两种ADMM-CSNet的主要不同之处在于reconstruction layer和network layers Z ( n ) \mathbf Z^{(n)} Z(n)的实现。
reconstruction layer:
- Basic-ADMM-CSNet 使用CS MRI,如命题1、2讨论
- Generic-ADMM-CSNet 使用CS观测矩阵进行快速矩阵求逆
network layers implementing Z ( n ) \mathbf Z^{(n)} Z(n)
- Basic-ADMM-CSNet 使用公式12的 Z ( n ) \mathbf Z^{(n)} Z(n)闭式解
- Generic-ADMM-CSNet 使用unfolded梯度下降迭代 Z ( n ) \mathbf Z^{(n)} Z(n),这进一步引入了用于增强网络容量的可学习参数。实现非闭式解。第6.1节所示,通用ADMMCSNet显著改善了CS-MRI的结果。
网络训练
-
paired数据:全采样x和欠采样观测y
-
损失函数:averaged normalized root mean square error (NRMSE)

-
可学习参数:
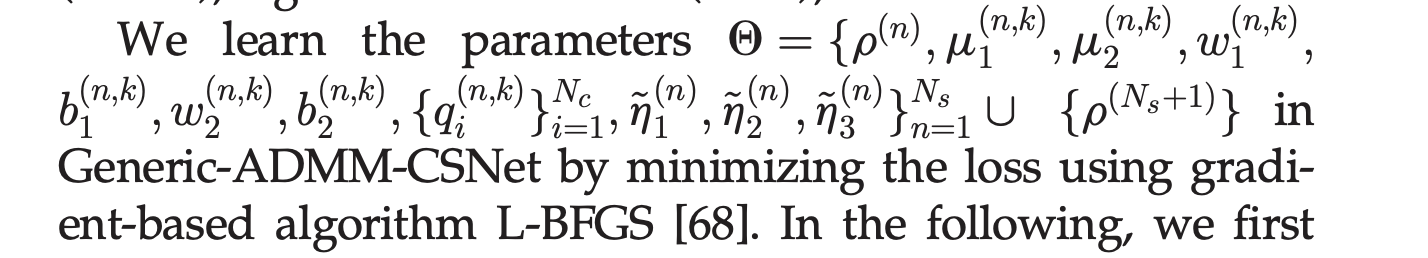
-
初始化:by model-based initialization method or random initialization method
- Model-Based Initialization:use a specific model to initialize
- random initialization such as Gaussian distribution initialization
参考资料
【1】【凸优化笔记7】-交替方向乘子法(ADMM) - 知乎 (zhihu.com)
【2】【凸优化笔记4】-4.3 软阈值算子