【形心】不规则多边形形心计算方法（含面积计算）

news2024/11/25 0:42:34

every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog

0. 前言

不规则多边形形心计算若干方法小结

说明： 这里以凹多边形为例，方便排查所计算坐标不在多边形之外。

1. 正文

1.1 方法一

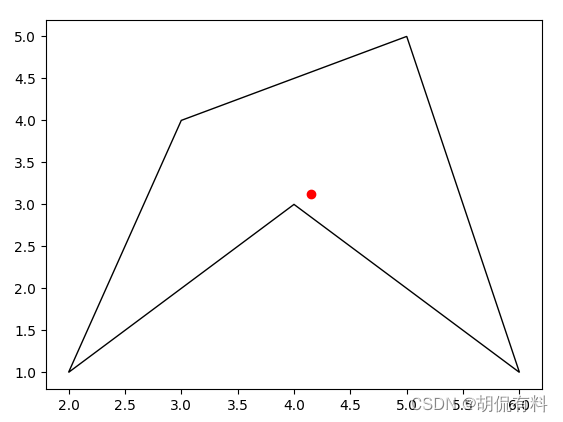
shapely Polygon 直接获取中心

import numpy as np
import matplotlib.pyplot as plt
from shapely.geometry import Polygon

# 定义凹多边形的顶点坐标
vertices = [(2, 1), (4, 3), (6, 1), (5, 5), (3, 4)]

polygon = Polygon(vertices)
centerx = polygon.centroid.x
centery = polygon.centroid.y

plt.figure()
polygon = plt.Polygon(vertices, fill=None, edgecolor='black')
plt.gca().add_patch(polygon)

plt.scatter(centerx, centery, color='red')
plt.show()

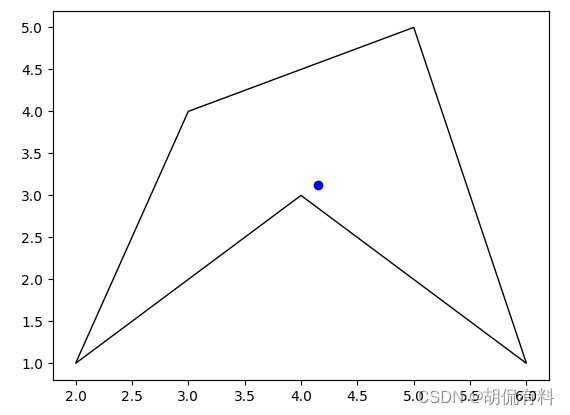
在这里插入图片描述

1.2 方法二

将凹多边形划分为若干个三角形。
对每个三角形，找到其重心（重心是三角形三个顶点的平均值）。
对所有三角形的重心进行加权平均，其中每个三角形的面积作为权重。

import numpy as np
import matplotlib.pyplot as plt

# 定义凹多边形的顶点坐标
vertices = [(2, 1), (4, 3), (6, 1), (5, 5), (3, 4)]

# 划分凹多边形为三角形
triangles = []
for i in range(1, len(vertices) - 1):
    triangles.append([vertices[0], vertices[i], vertices[i+1]])

# 计算每个三角形的面积和重心
areas = []
centroids = []
for triangle in triangles:
    x1, y1 = triangle[0]
    x2, y2 = triangle[1]
    x3, y3 = triangle[2]
    
    area = 0.5 * ((x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1))
    centroid_x = (x1 + x2 + x3) / 3
    centroid_y = (y1 + y2 + y3) / 3
    
    areas.append(area)
    centroids.append((centroid_x, centroid_y))

# 计算形心中心
total_area = np.sum(areas)
center_x = np.sum([area * centroid[0] for area, centroid in zip(areas, centroids)]) / total_area
center_y = np.sum([area * centroid[1] for area, centroid in zip(areas, centroids)]) / total_area

plt.figure()
polygon = plt.Polygon(vertices, fill=None, edgecolor='black')
plt.gca().add_patch(polygon)
plt.scatter(center_x, center_y, color='blue')
plt.show()

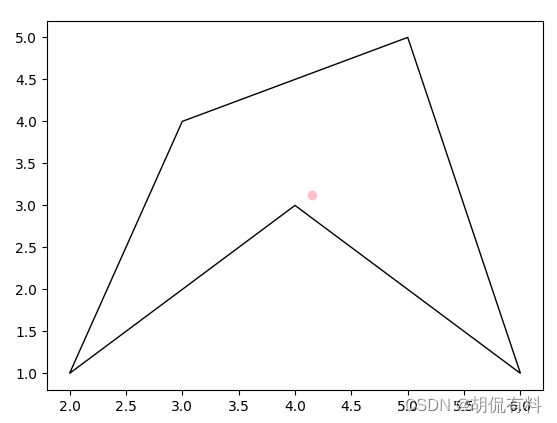
在这里插入图片描述

1.3 方法三

面积公式：
面积使用高斯面积公式，即，鞋带公式，

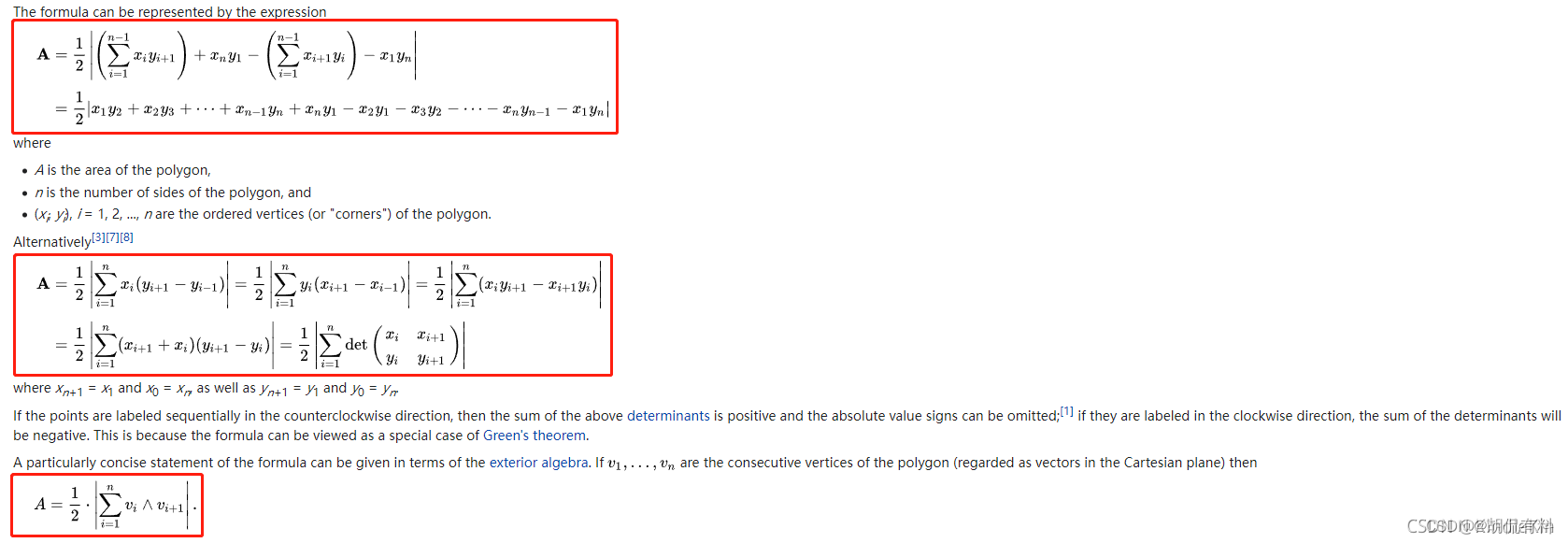
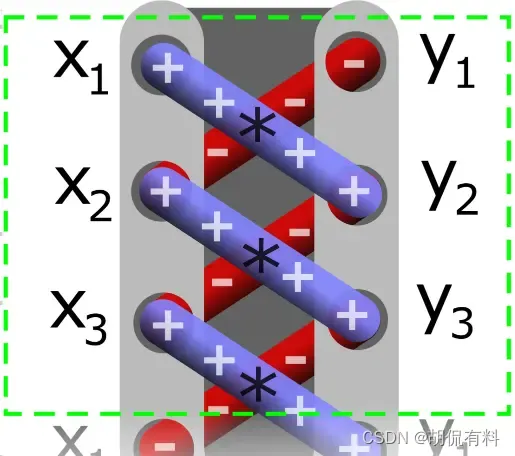
请添加图片描述

请添加图片描述
形心公式：

请添加图片描述

import numpy as np
import matplotlib.pyplot as plt

# 定义凹多边形的顶点坐标
vertices = [(2, 1), (4, 3), (6, 1), (5, 5), (3, 4)]


def cal_area(vertices):  # Gauss's area formula 高斯面积计算
    A = 0.0
    point_p = vertices[-1]
    for point in vertices:
        A += (point[1]*point_p[0] - point[0]*point_p[1])
        point_p = point
    return abs(A)/2


def cal_centroid(points):
    A = cal_area(points)
    c_x, c_y = 0.0, 0.0
    point_p = points[-1]  # point_p 表示前一节点
    for point in points:
        c_x += ((point[0] + point_p[0]) *
                (point[1]*point_p[0] - point_p[1]*point[0]))
        c_y += ((point[1] + point_p[1]) *
                (point[1]*point_p[0] - point_p[1]*point[0]))
        point_p = point

    return c_x / (6*A), c_y / (6*A)


points = np.array(vertices)
x, y = cal_centroid(points)

plt.figure()
polygon = plt.Polygon(vertices, fill=None, edgecolor='black')
plt.gca().add_patch(polygon)

plt.scatter(x, y, color='pink')

plt.show()