目录
- 1、 比例控制系统的标准结构
- 2、最简单的例子
- 3、第二个例子
- 4、积分控制器
- 6、微分控制
- 7 总结
今天 看到了B站上一个叫洋葱auto的UP主搬来的介绍PID控制的视频,感觉讲得形象易懂,为便于让和我一样看了无数文章还是不能很好理解PID控制本质的人共同分享,这里整理成笔记。以便翻阅。
阅读本篇之前,应该对PID有一个最基本的了解。至少要知道PID是什么,用途是什么。
以下是百度百科里的内容:
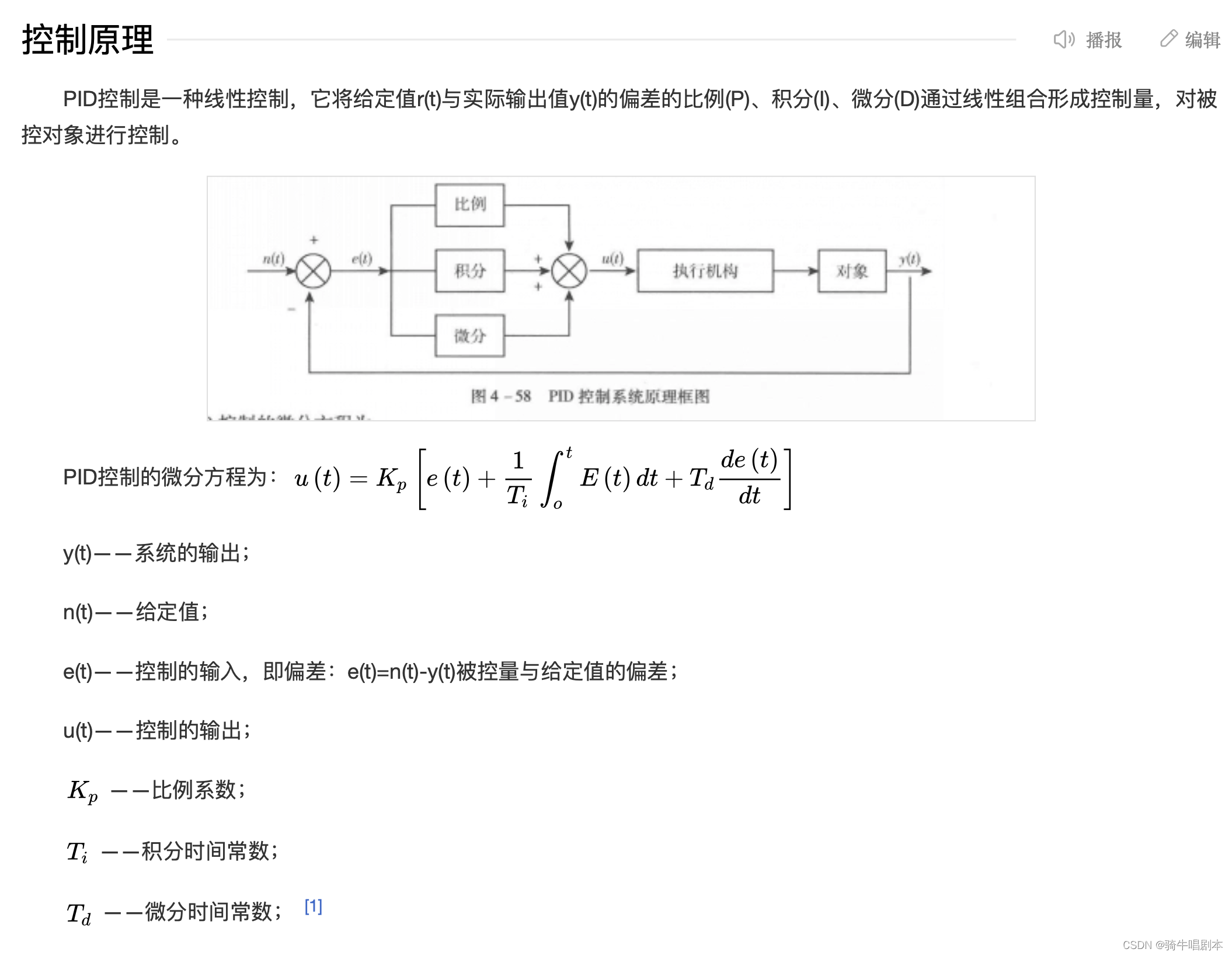
\qquad 在工业过程控制中,按被控对象的实时数据采集的信息与给定值比较产生的误差的比例、积分和微分进行控制的控制系统,简称PID(Proportional Integral Derivative)控制系统。
\qquad PID控制技术结构简单,参数调整方便,其实质是根据输入的偏差值,按比例、积分、微分的函数关系进行运算,运算结果用以输出进行控制。它是在长期的工程实践巾总结出来的一套控制方法,实际运行经验和理论分析都表明,对许多工业过程进行控制时,这种方式都能得到比较满意的效果。
好吧,有点学术精神,努力看,还是看不懂的话。那下面来做一个比较形象的有具体解释。
1、 比例控制系统的标准结构
先从比例控制(Proportional )标准框架说起,直接上图:
图(1.1)
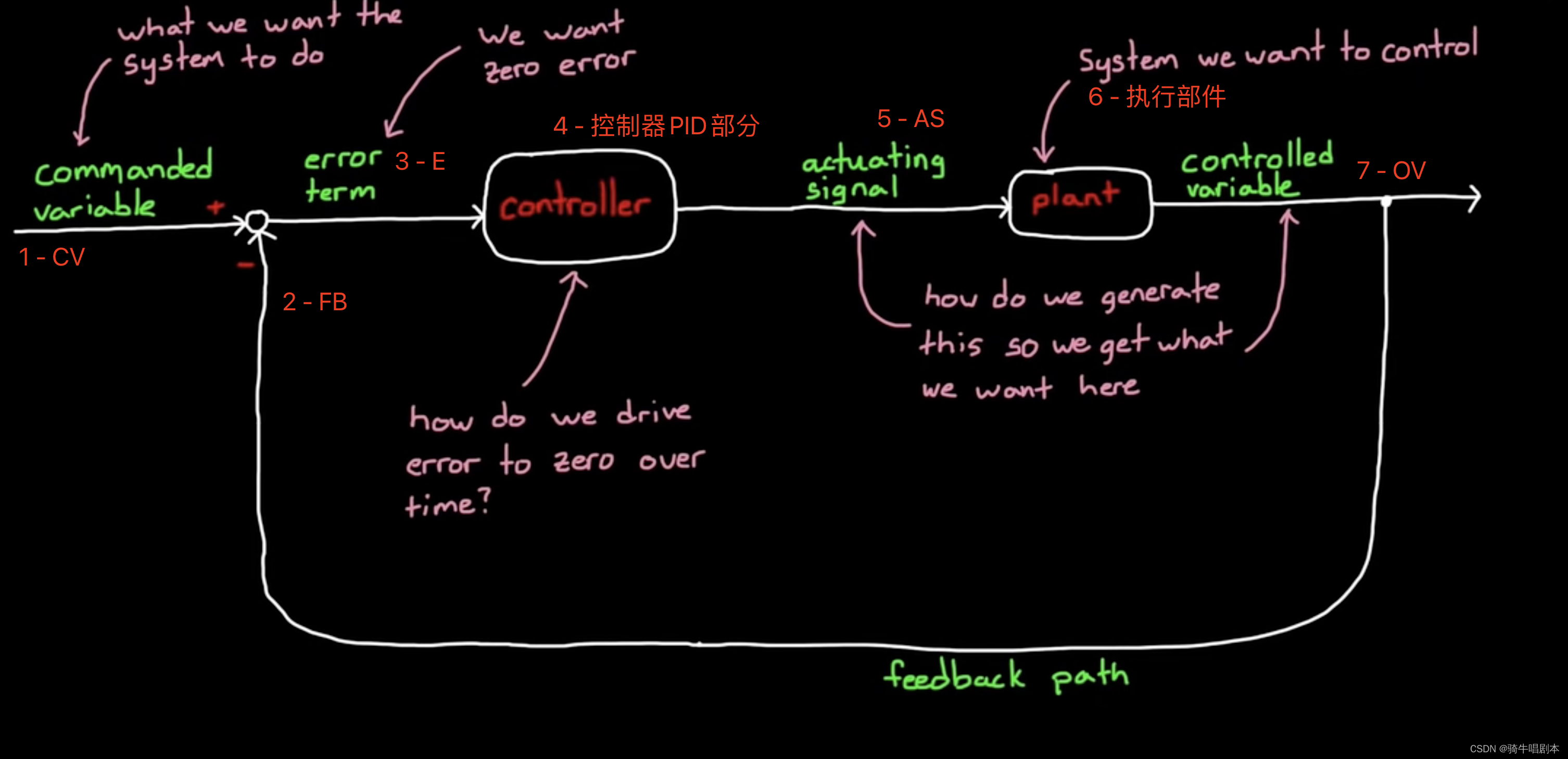
按理解的顺序来解释上方的结构:
图(1.2)
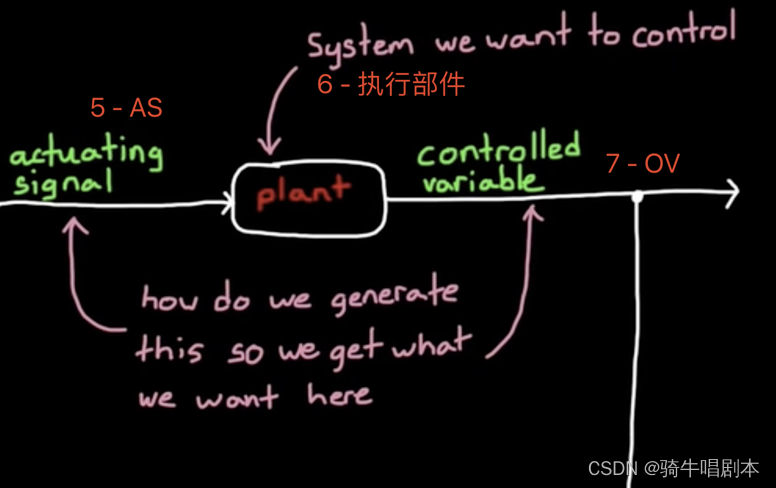
- 6 - 执行部件 :一个系统或设施,总要有一个执行部件,如电机,加热丝,等等负责动作的部件。
- 7 - OV:受控的输出量。比如,转速,流速,温度,距离,高度等等执行结果量。
- 5 - AS:驱动信号量,比如PWM,电流,电压等可以控制执行部件执行的信号。
以上三个部件,其实就组成了我们一般意义上的一个系统或设施。这是没有加上PID控制的系统。
而一个系统的正常运行,必须根据输出(OV)的效果来调整驱动信号(AS),如温度太高了,要降低电流,转速太快了,要减少电机转速,就需要降低PWM信号的占空比等。因此,在上方图(1.2)的基础上就要加上控制器,反馈,误差比较单元等。
如图(1.3)
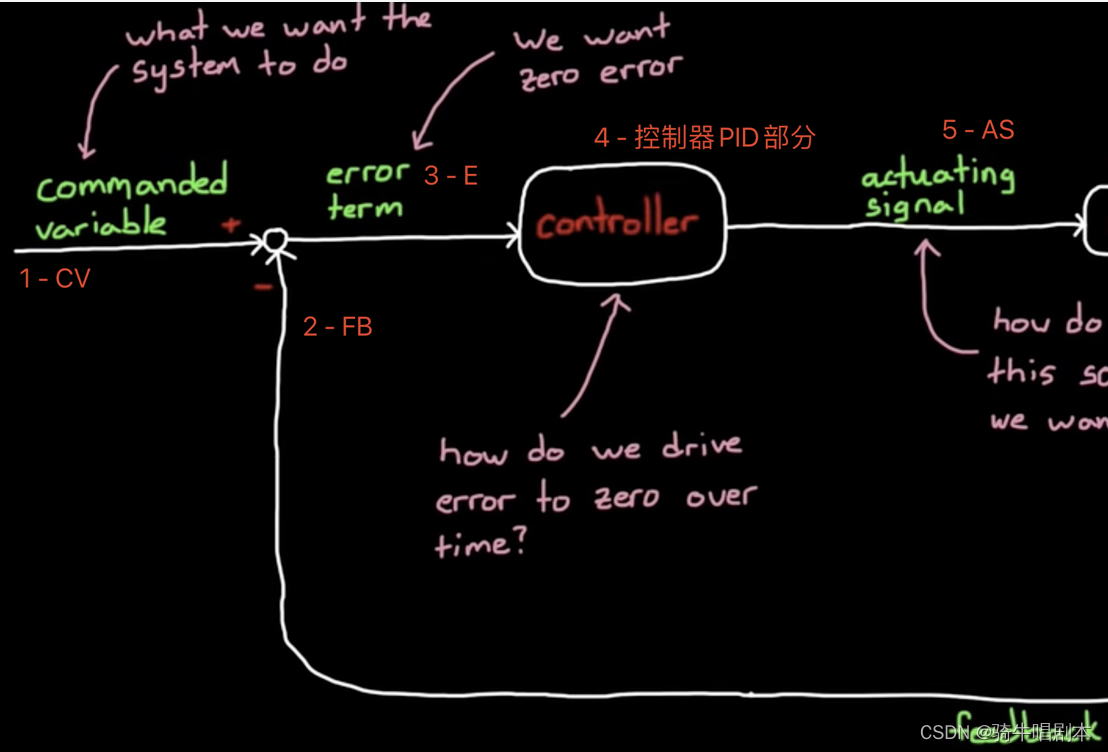
- 1- CV :目标量,即希望执行结果OV达到一个什么样的目标量值。如:速度达到100公里/小时,温度达到100度,距离为0等等。
- 2 - FB :反馈量,即当下执行的结果量。如:当下速度为50公里/小时,当下温度为50度,当下距离为10米等等。
- 3 - E :误差项,即CV-FB得到的当下值与目标值的差值。
- 4 - 比例控制器:即,比例控制的算法部分,通过将误差项通过乘以一个增益系数Kp算法计算,然后输出驱动信号(AS)的控制环节。
\qquad 因此,到这里,就把比例控制的实际结构简单的介绍完成了。这个结构是一个完整的闭环控制结构。重点要知道,一个控制系统和人的行为一样,要通过不断的反馈来修正驱动信号,使结果与目标不断接近,并最终实现误差项为0。
2、最简单的例子
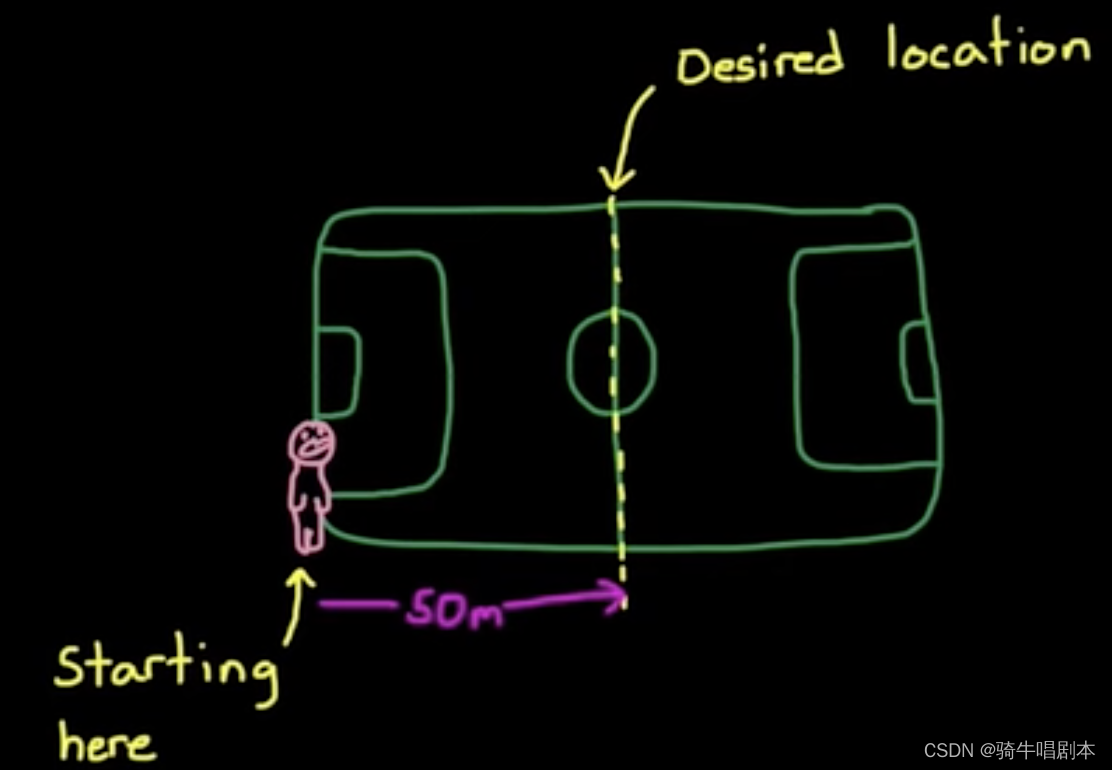
以上,仍然比较抽像,这里举一个最简单的例子,如图(2.1),你在球场的一端,要走到50米的目标位置。则你现在是处在起点,0米位置。
图(2.1)
如果对应到图(1.1)的控制结构图里,则如图(2.2)
图(2.2)
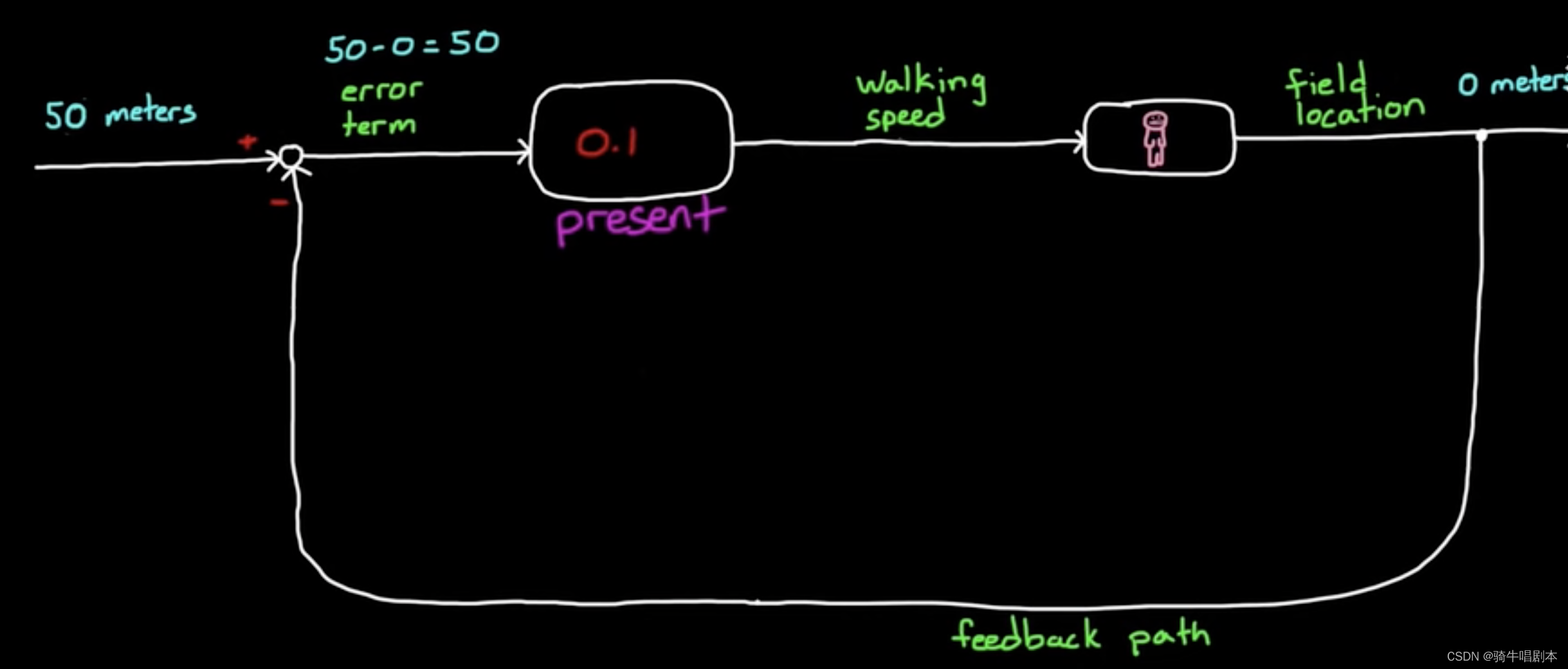
- plant:你就是那个执行机构plant;
- OV:受控量(或者叫输出量OV)就是你现在行走的距离;
- CV:命令变量或目标量就是50米;
- FB:就是当下你已行走的距离,在这个例子里,FB = OV,初始0时刻时,FB = OV = 0米;
- E:就是误差项,这里E = CV - FB。初始状态0时刻时,E = 50 - 0 = 50米;
- 控制器参数:假设选定比例增益Kp = 0.1。则在控制内相当于执行了一个算法 使得控制器的输出Actuating Signal(驱动信号AS)满足如下的公式 AS = Kp* E = Kp * (CV - FB) 初始状态时 AS = 0.1 * 50 = 5米/秒。(注意:这里的公式是一个伪公式,也就是说严格意义上,公式本身并不能在这里实现AS的值的单位为“米/秒”,只是为了说明以上这个问题,在数值上我们借用了这个公式的计算规则而已。)
- AS:这里驱动信号为一个行走速度的量。单位为“米/秒”;具体算法,如上所述。
\qquad
因此,一旦你开始行走,则以上的量就会出现随时间t出现变化。
图(2.3)
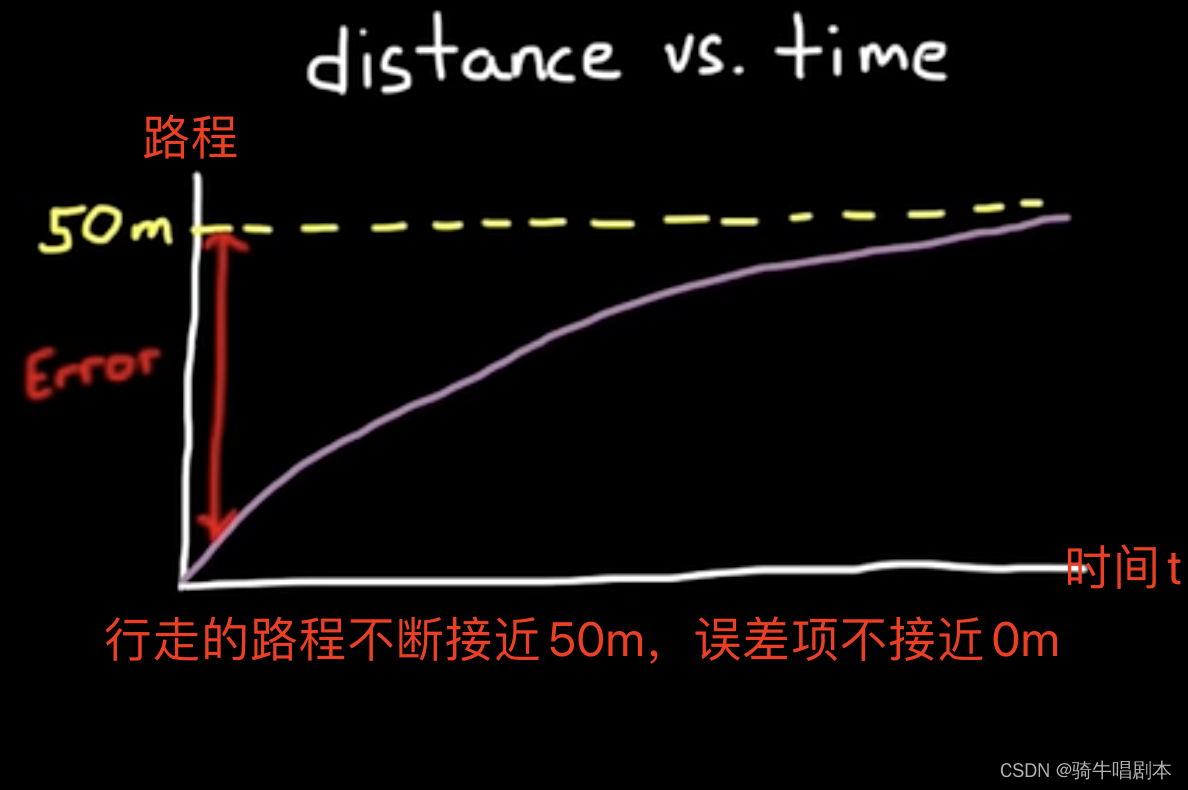
图(2.4)

从以上图2.3 图 2.4可以看出。
- 当t=0时,误差E = 50m,这时,速度值为AS = Kp * E = 0.1 * 50 = 5米/秒。
- 当t=1时,FB = 5米/秒*1 秒= 5米。则此时,速度值 AS = Kp * E = 0.1 * (50 - 5) = 4.5米/秒。
- 当t=2时,FB = 5米 + 4.5米/秒 * 1秒 = 9.5米,则速度值AS = Kp * E = 0.1 * (50 -9.5) = 4.05米/秒。
- …
以此,可以看出几个量的趋势。随着FB越来越大逐渐靠近50米,误差量E也逐渐接近0,而速度也越趋于0。当到达50米的目标位置后,误差为0,速度也为0,则人会停在50米的这个目标位置处。
\qquad 以上完整的演示了,人这个系统走到某个目标位置时,控制系统如何发挥作用,以及过程当选定了某个增益Kp时的控制过程趋势。
\qquad 当然,从公式上看,就可以轻易得出,如果调整比例增益,就可以调整到达目标值的时间。其趋势图如下:
图2.5
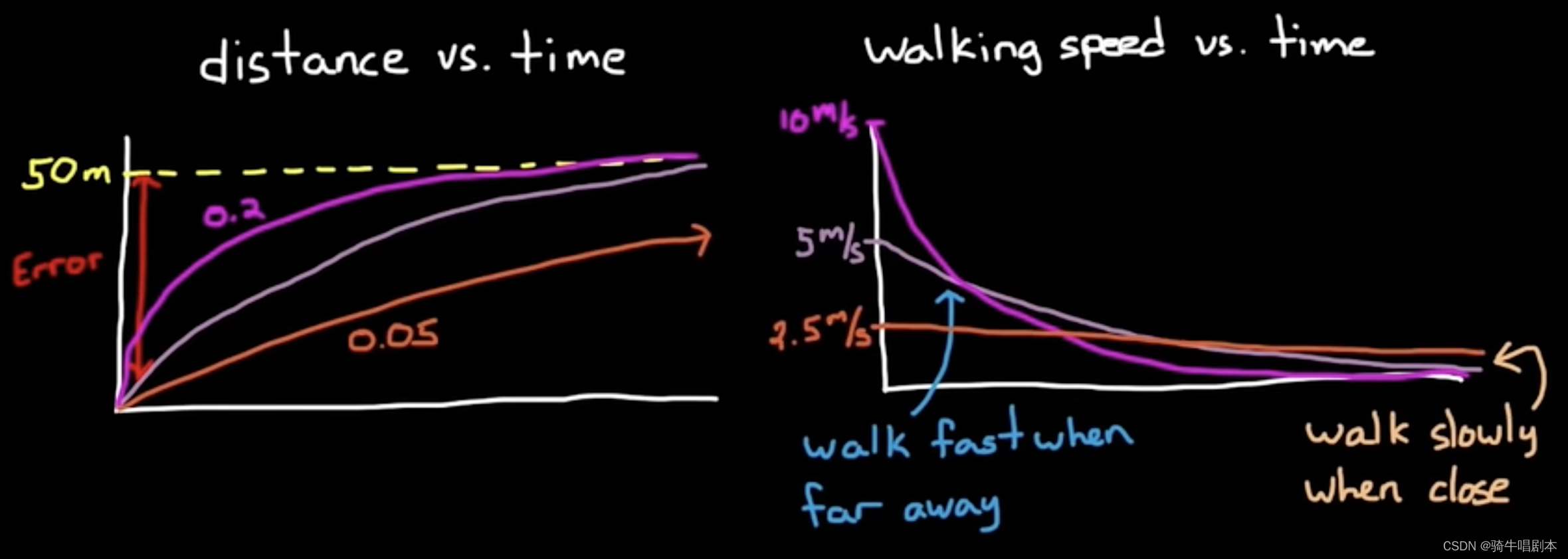
这里粗略的在一张图中分别表达出当增益为0.2 0.1 0.05时的各个量的趋势。
总结来说,对于如上所述的这个系统,一个简单的比例控制算法,就可以收到比较好的效果。但是如果对于其它系统,这个简单的单一比例控制算法不一定会收到较好的效果。
3、第二个例子
设计一个四旋翼无人机的高度控制器。与上例类似,该四旋翼无人机从地面起飞,要达到50米的高度,并旋停在这个高度。如下图:
图3.1

在这个例子中,控制系统结构会有所改变。如下图:
图3.2

在这里,执行机构换成了四旋翼机,驱动信号变成了螺旋桨转速,受控的输出量变为海拔高度。
\qquad 在这个无人机的控制系统里,如果只采用如上的比例增益控制方式。会出现什么情况呢?
- 首先,当初始时刻,海拨高度为0(即OV = FB = 0),则误差E = CV - FB = 50。这时,在AS = Kp * E时将产生很大的螺旋桨速度,无人机将快速上升。然后随着高程的增加,无人机螺旋桨速度逐渐下降,高程继续增加。直到高程达到50米的设定值。因此理想状态,如下图3.3所示。
图3.3
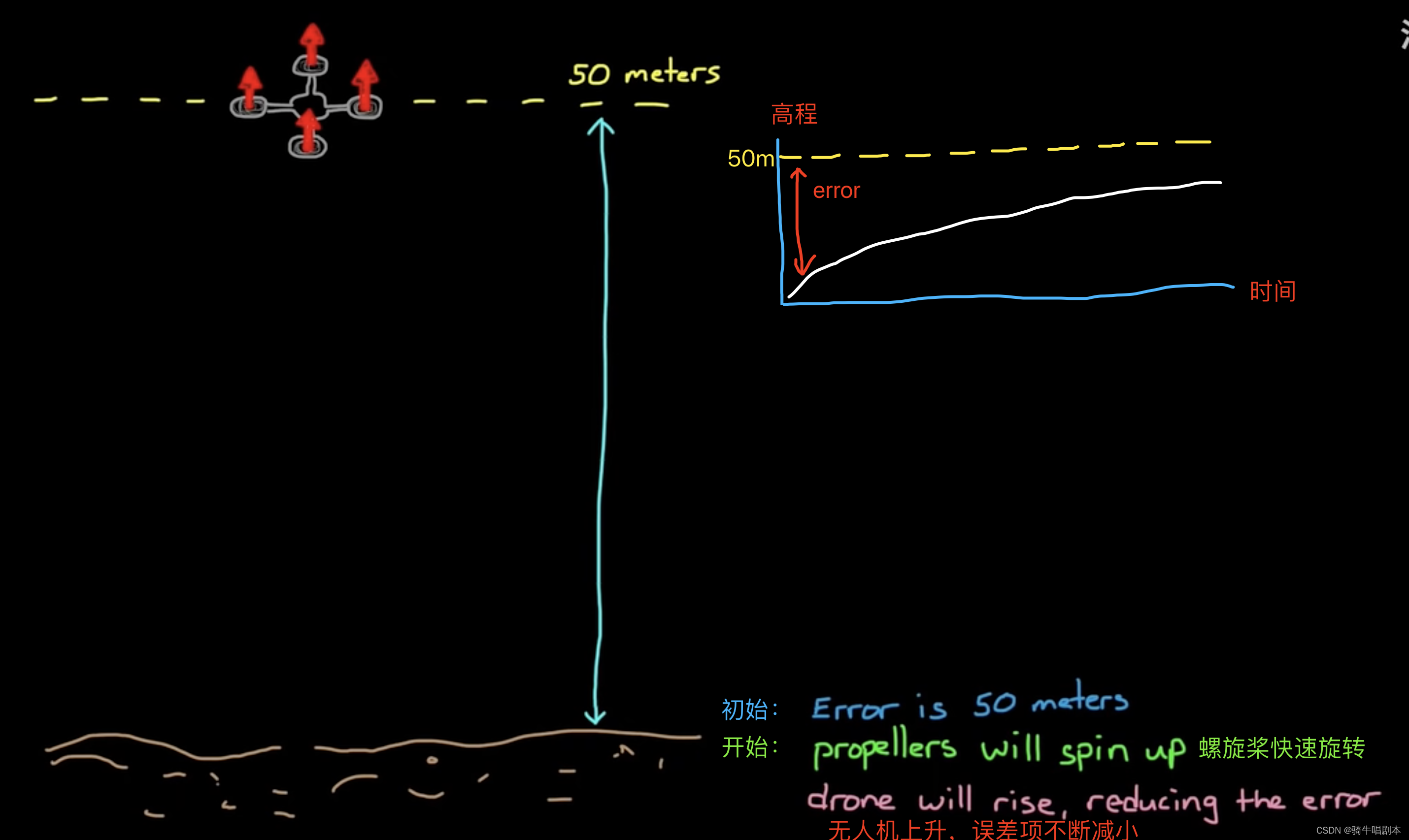
- 其次,当无人机到达50米的目标高程,这是理想化的状态,实际上,是不可能的。这里来看看假设当无人机到达了50米的高度后。这时,E= CV - FB = 50 - 50 = 0。因此,螺旋桨转速 AS = Kp * E = Kp * 0 = 0。则无人机将因为没有升力而下跌。如图3.4
图 3.4
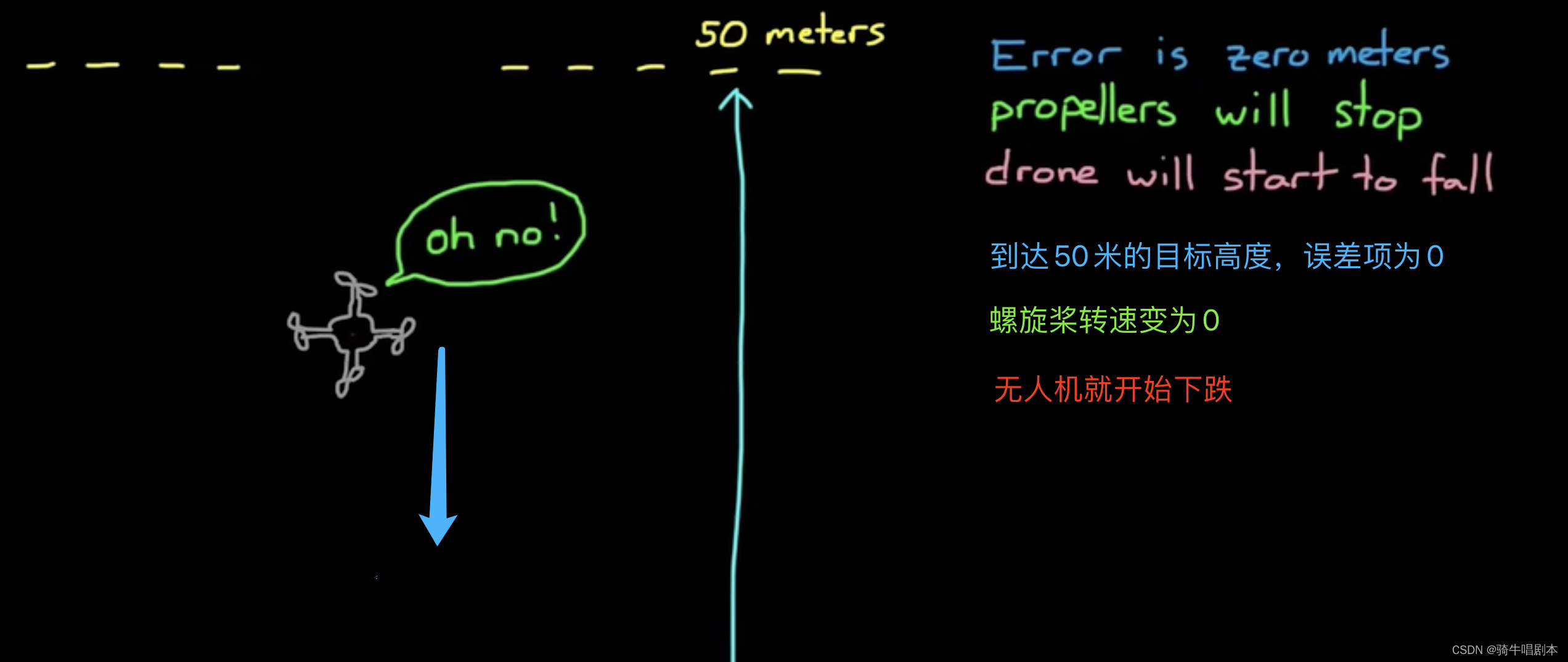
- 这时,随着无人机下落,高程低于50m后,误差项将再次出现,于是,螺旋桨将再次旋转产生生力。无人机就会重新上升。在这个不断的下落与上升中会产生一个平衡。我们假设使无人机处于旋停的状态时,螺旋桨的转速正好处于100rpm(每分钟100转)的状态。因此把这个叫旋停转速。
- 至于无人机最终会旋停在哪个高度,则是根据设定的不同的比例增益数值来确定的。如下图3.5里的计算可知,如果选择不同的比例增益(Gain 即Kp)数值,根据公式 AS = 100rpm = Kp * E 可以计算出误差项E。当增益值Kp = 2 时,则E = 50,则意味着无人机此时误差项为50米,那么就还停留在地面处。其它的计算可以参看图例。这里需要强调一点,不论选择什么Kp,都不可能消除误差,也就是无人机永远无法准确旋停在目标高度。
图3.5
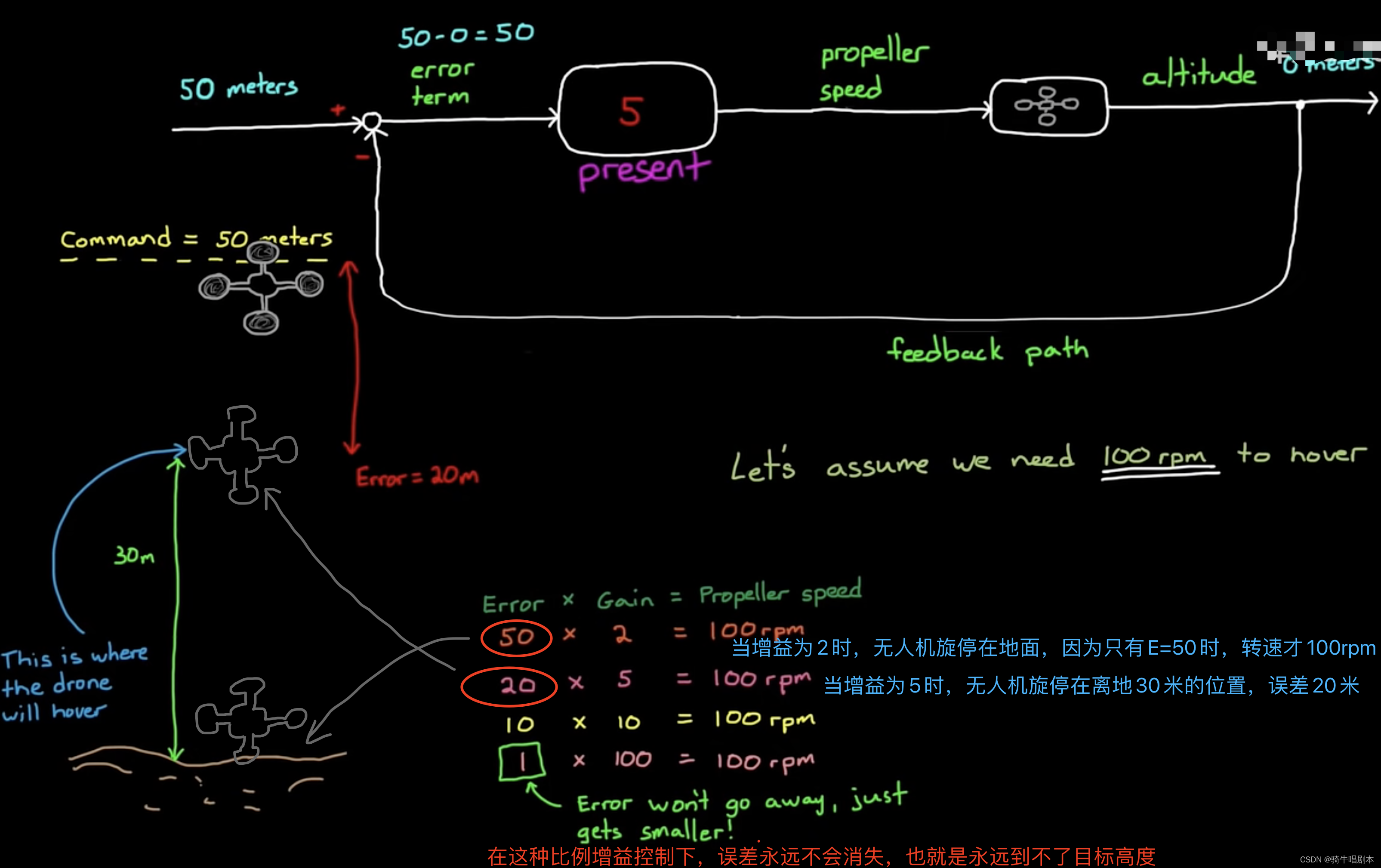
因此,上例说明,比例增益控制器,并非在所有应用场景都 适用。它对第一个步行的例子可用,但对无人机的这个例子,则会产生衡定的误差。这个误差称为稳态误差。
4、积分控制器
\qquad
所以,如何调整控制器,去消除稳态误差。这里就需要引入另一个控制器–“积分控制器”。
\qquad
所谓的积分控制器,其本质是将过去一段时间以来的所有误差项进行累加然后输出这个累加值进行控制。所以,当输入的误差项持续为正值时,积分项也将是一个累加后的正值,当误差项开始出现负值时(比如,无人机高度高于目标高度后,误差项就是负值),则积分项将开始减小,如果误差项持续为负值,则积分项将持续减小。如果误差项持续为0,则此时开始积分项将不再改变,保持一个衡定值。
图4.1
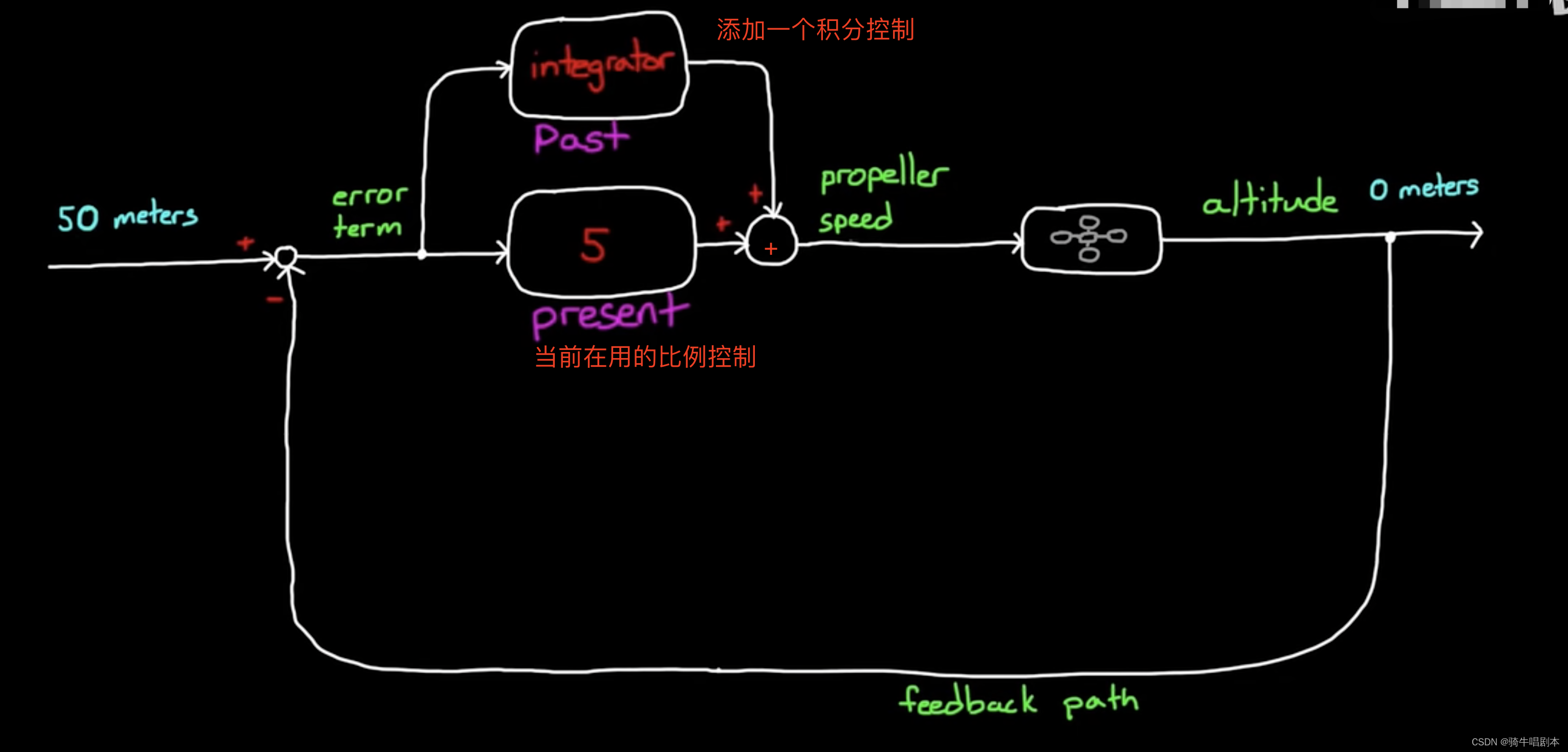
\qquad 当积分控制加入到系统后。将使系统产生更快的响应,并消除稳态误差。具本的控制过程如下所示:
图 4.2
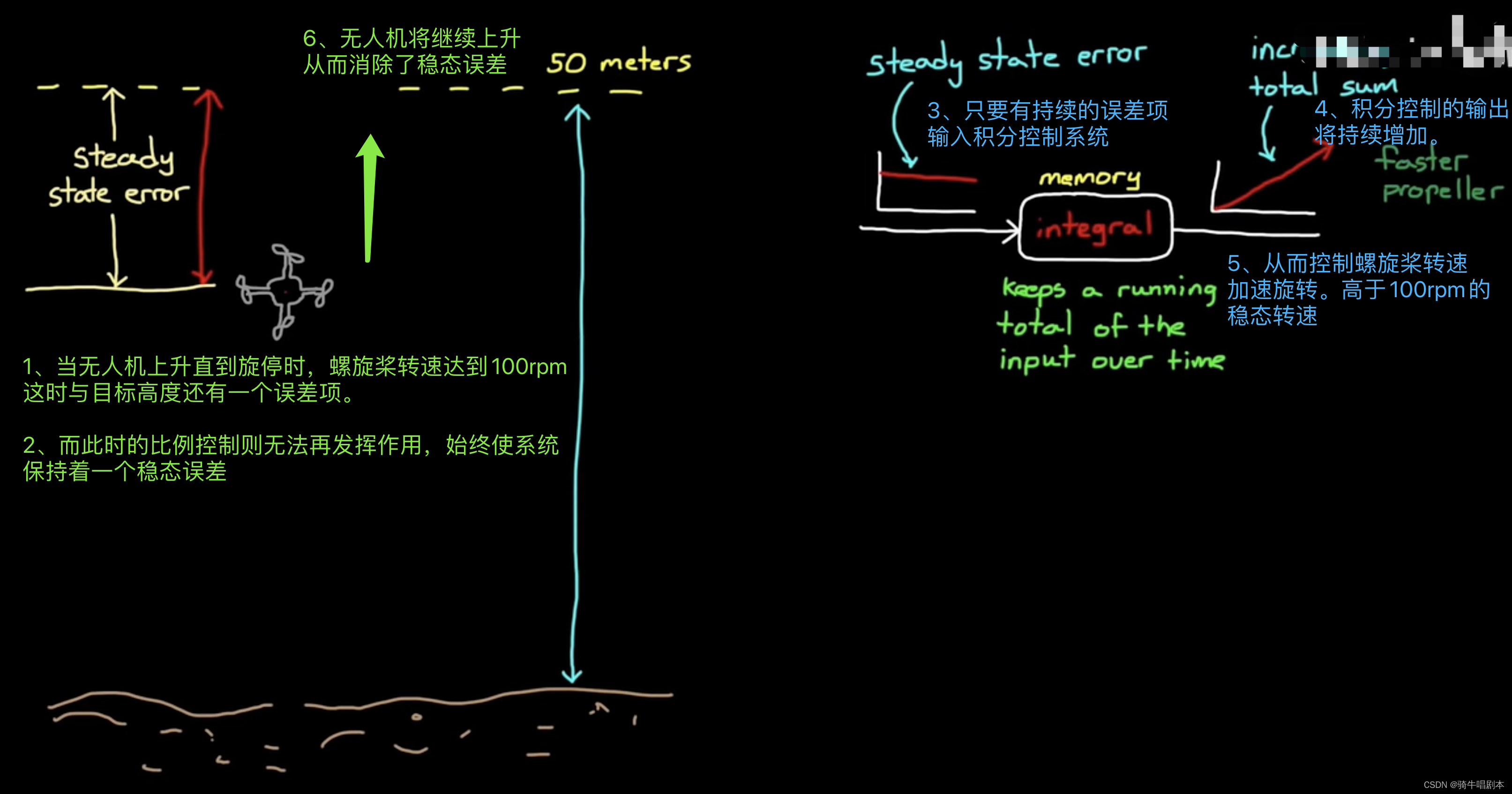
\qquad 在上图4.2中,为了突显积分控制的作用,这里没有画出比例控制器。但实际,在无人机达到稳态误差前的一段时间里,主要是比例控制器在起作用。在到达稳态误差的高度时,比例控制就无法再使无人机进一步上升,这时积分控制就开始为主发挥作用了,积分控制螺旋桨转速进一步加速,无人机继续上升。
\qquad 无人机继续上升,在无人机接近目标高度50米,这时,误差很小了,则比例控制输出已接近为0。而积分控制由于是不断累加过去的误差,在此时积分项仍为一个较大的正值,将继续增大螺旋桨的转速,使无人机螺旋桨的转速远大于100rpm的旋停转速,因此此时会使无人机飞越50米的目标高度。从而产生过冲行为。如图4.3
图4.3
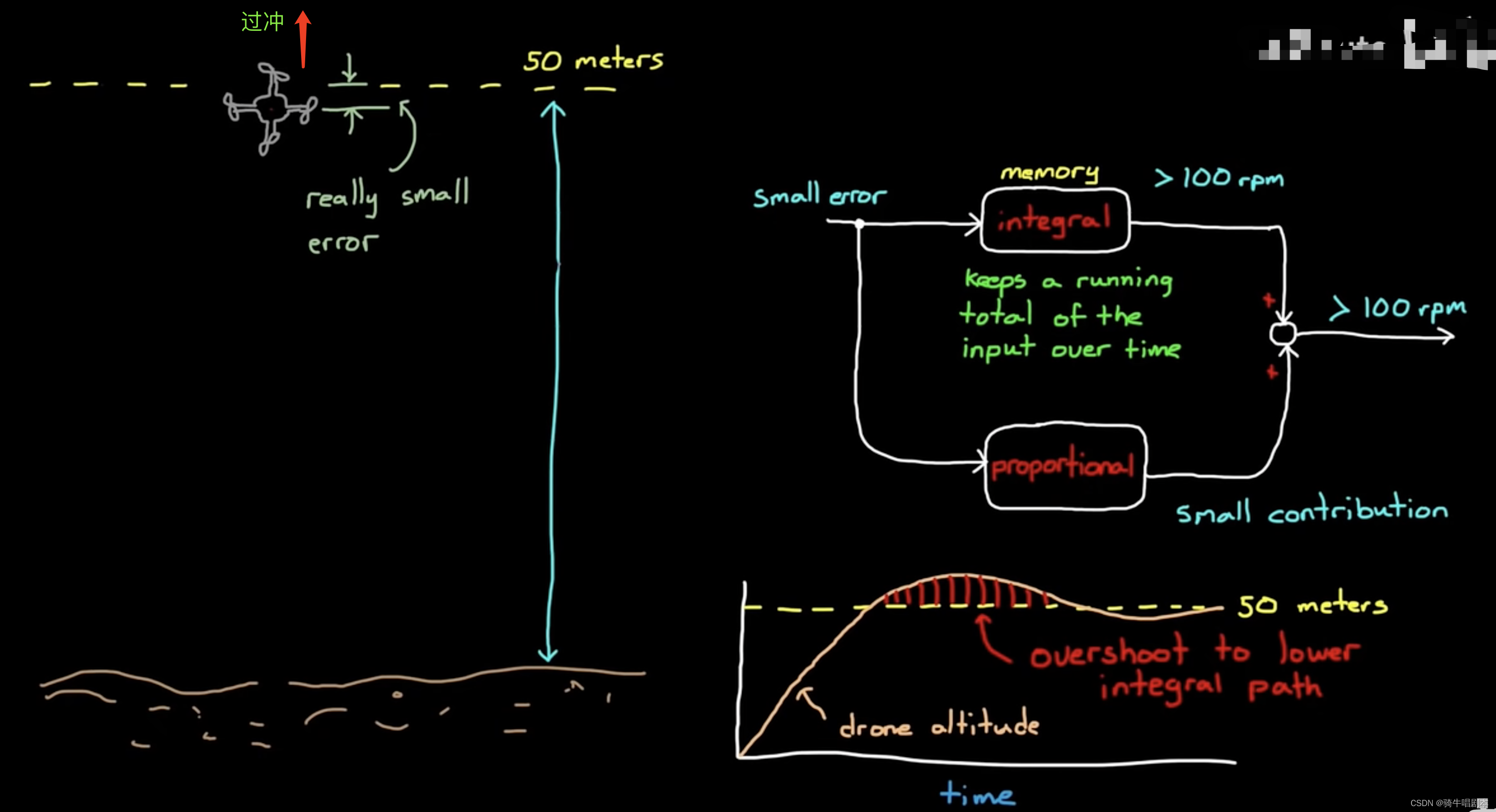
\qquad 在过冲后,FB就会大于50米,因此误差项就会变为负值(E = CV - FB )。而积分项去累加负的误差项后,就会使积分控制的输出-螺旋桨转速开始下降,比如低于100rpm,则无人机就会下降,并低于目标高度50m,于是误差项又增加了,积分控制输出的螺旋桨转速又提高,使无人机上升…。这样,无人机就会在积分项的控制下不断的在50米这个目标高度附近做上下的运动。这个运动就像是一种围绕着目标高度的振荡一样。这个振荡的振幅会越来越小,并最终使无人机旋停在50米处。此时,由于误差项为0,则积分控制也将不再发生变化,会稳定在某个值上。这个振荡的过程,称为“超调”。
6、微分控制
\qquad 比例控制会产生稳态误差,这时,我们加入积分控制来消除这个稳态误差。但是积分控制又会产生“超调”。那么要消除这个超调,就要用到PID控制中的这个D - “微分控制(Derivative)”。
图6.1
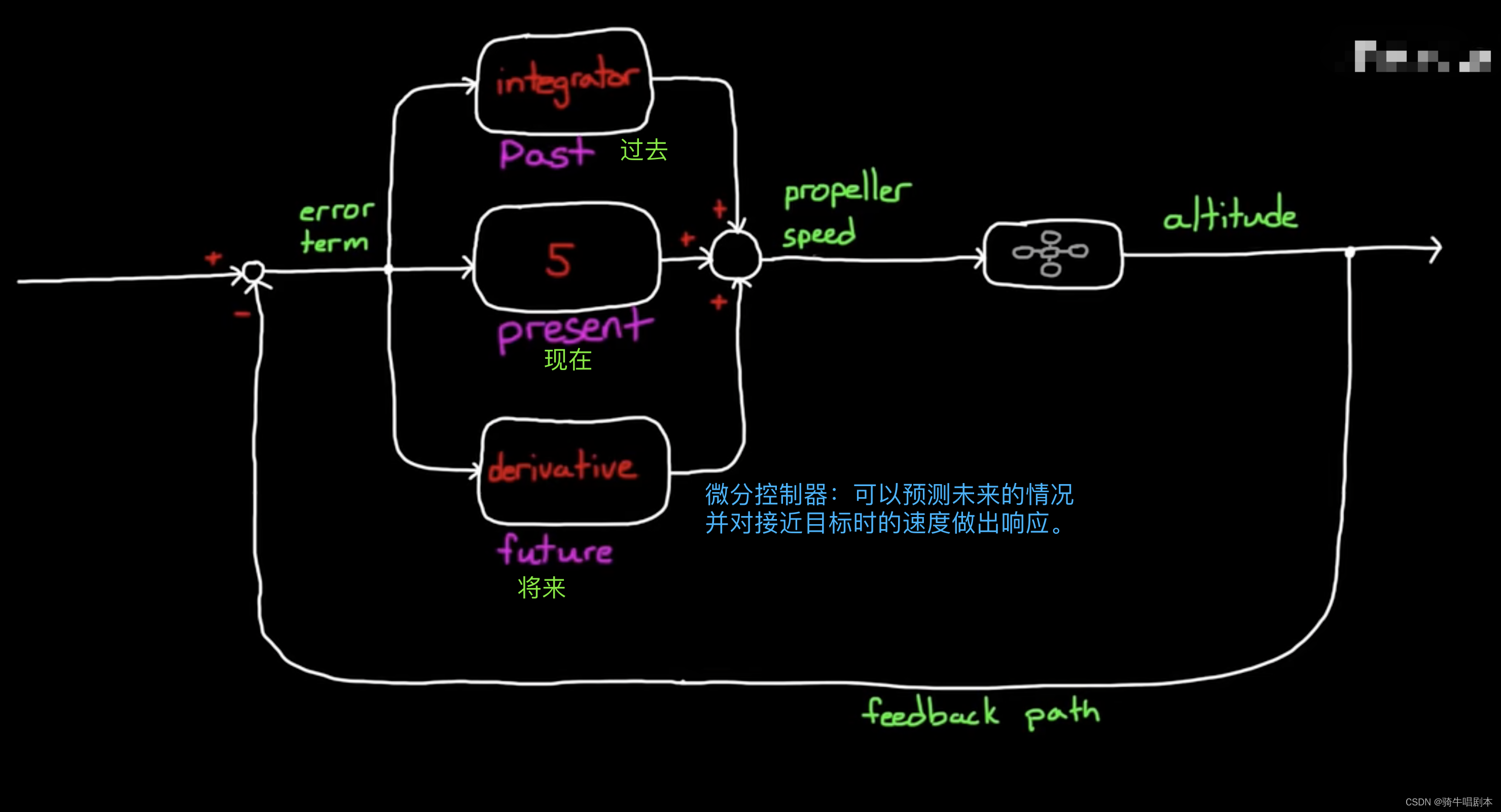
\qquad 微分的计算过程是用现在误差减去上一次的误差,然后除以时间。这里可以看出微分控制的本质是反应当下误差的变化率,由于误差的变化是一个连续的过程(即连续函数)一般不会出现断崖式的变化(即分段函数),因此当下的变化率也可以反应出未来某一段时间的可能的变化率趋势的。在具体计算时,根据微分的定义可以知道,当误差持续减小时,将产生负的变化率,微分控制呈现出负值,当误差持续增大时,将产生正的变化率,微分控制呈现出正值。
\qquad 所以说,在无人机例子中引入微分控制器,可以预测未来的情况,并对接近目标高度时的飞机速度做出响 应。
图6.2
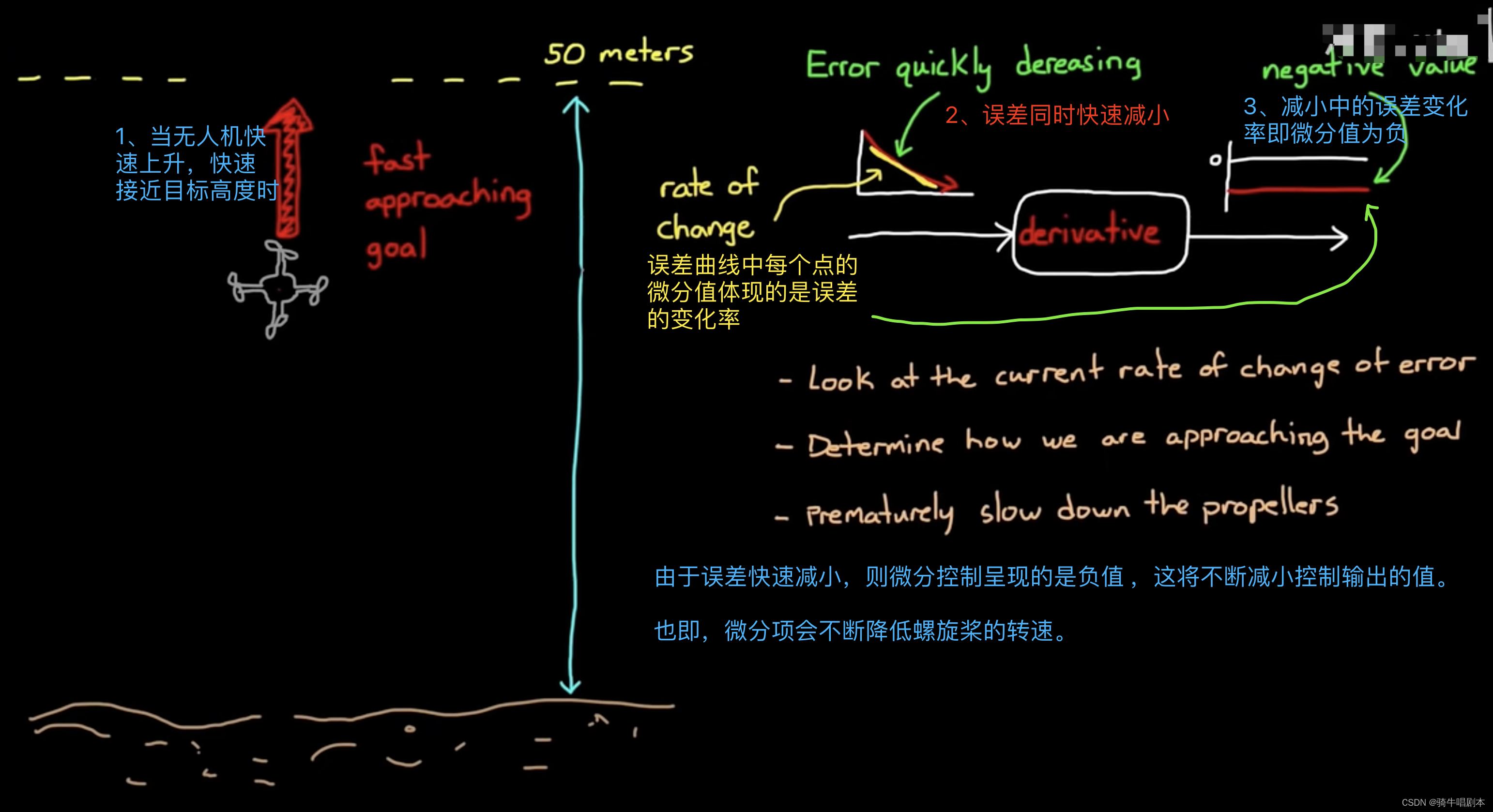
如上图6.2,微分控制在误差持续减小的过程中呈现出负值,该负值将加到控制器的输出中,这将使螺旋桨的转速减小。控制器通过误差变化率,得知系统接近目标的速度过快,因而提前降低螺旋桨的速度。从而防止无人机过冲。
7 总结
比例§控制能迅速反应误差,从而减小稳态误差。但是,比例控制不能消除稳态误差。比例放大系数的加大.会引起系统的不稳定。
积分(I)控制的作用是:只要系统有误差存在,积分控制器就不断地积累,输出控制量,以消除误差。因而,只要有足够的时间,积分控制将能完全消除误差,使系统误差为零,从而消除稳态误差。积分作用太强会使系统超调加大,甚至使系统出现振荡。
微分(D)控制可以减小超调量,克服振荡,使系统的稳定性提高,同时加快系统的动态响应速度.减小调整时间,从而改善系统的动态性能。
图7.1
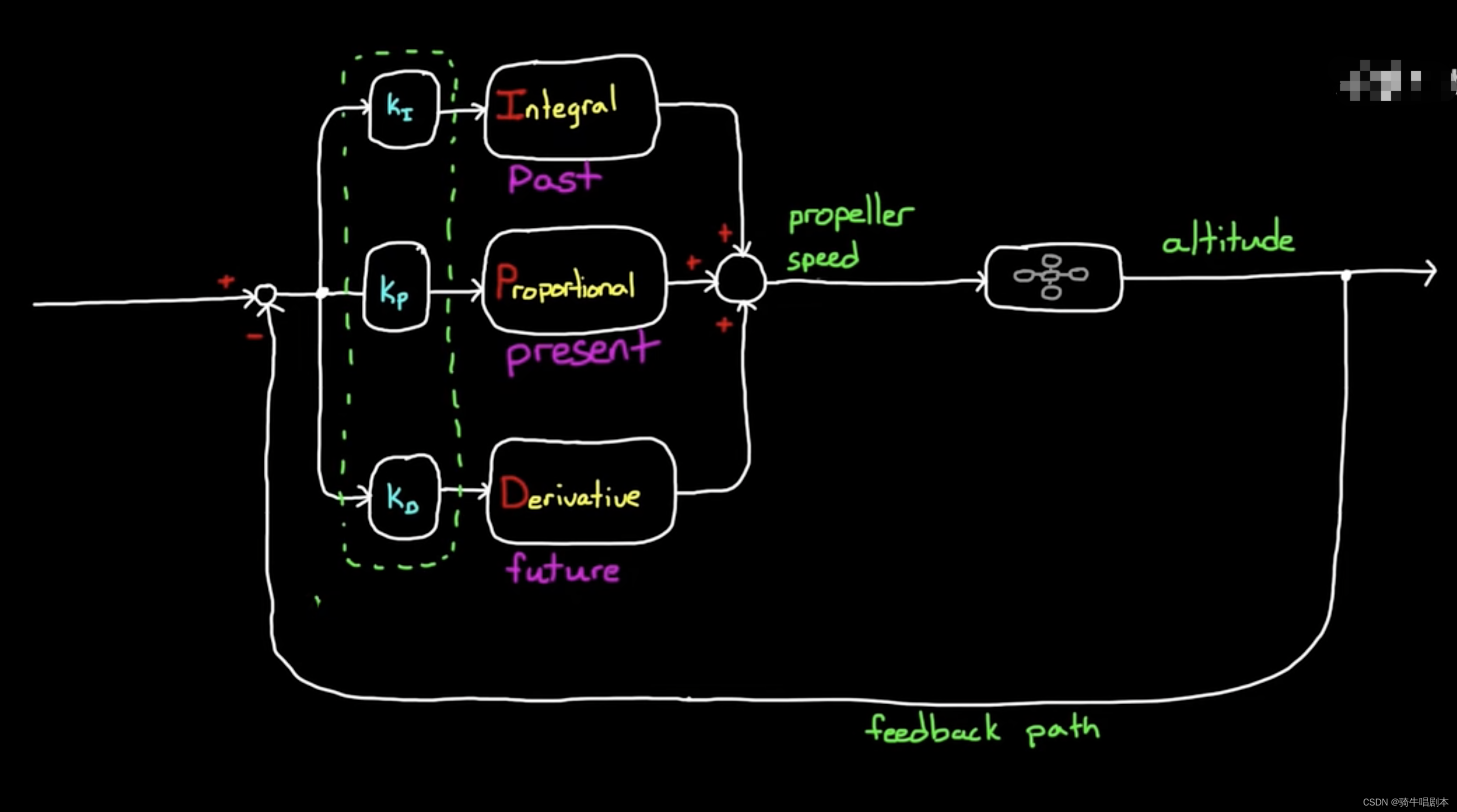
\qquad 对于三个P、I、D三个通道,再施以三个增益分别为KI、Kp、Kd,从而达到通过调节每个通道的增益来调节每个通道的影响大小。
根据不同的被控对象的控制特性,又可以分为P、PI、PD、PID等不同的控制模型。这里只需要把不用的通道的增益设为0即可以实现不同的控制模型。