一.二分查找

原题传送门：力扣

题目：

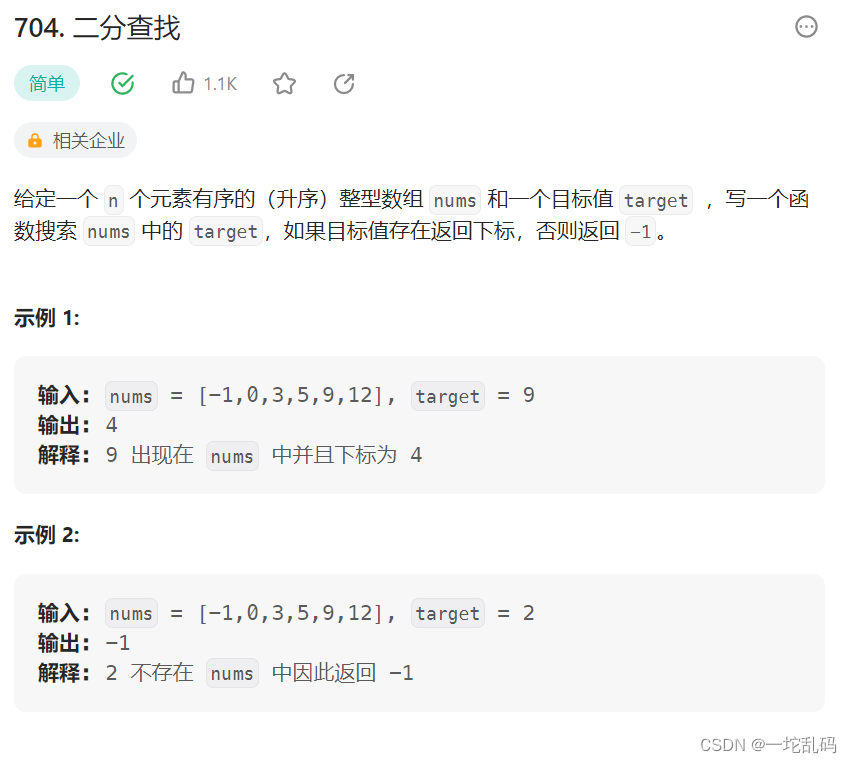
在有序序列中查找，用二分的方法是非常有效的，但仅限于有序，如果是无序，二分查找是用不了的。

现在我直接来讲思路，在下面这个序列中找到8这个数字，并返回它的下标：

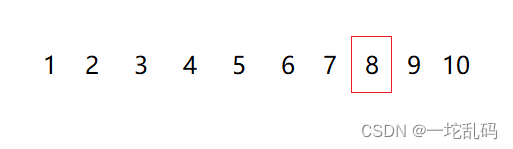
现在重点来了，先定义两个变量left,right来代表数组中的下标：

在定义一个变量，表示的也是下标，但它指向的元素是left,right指向的元素中间的位置：

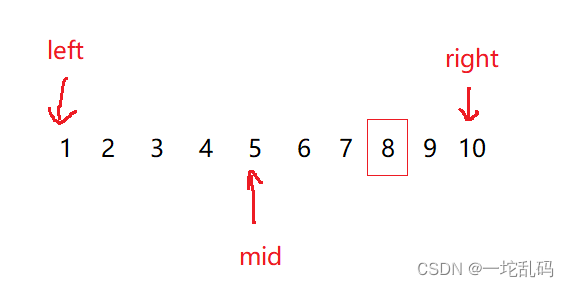
现在判断要找的值(我们用key来表示，这里的key为8)和mid指向的元素哪个大，如果key>a[mid]是不是说明我们要找的值肯定在mid的右边，同理如果key<a[mid]说明要找的值肯定在mid左边。这里可以看到key是在mid右边。现在我们就可以更新一下left的值：

//把left更新到mid的左边一个位置上
left = mid + 1;

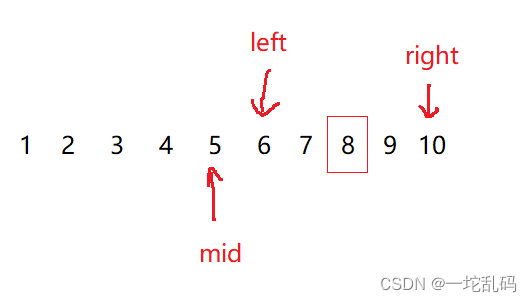
更新完left的值后，在更新mid的值，这里mid同样为left,right中间的位置：

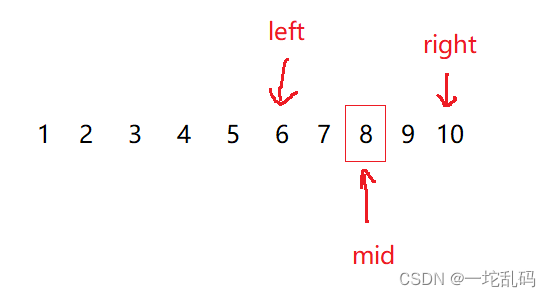
此时发现mid指向的刚好是key的值，这时候说明找到该值了，因为要直到下标，而下标就是mid的值。

但是如果现在key的值是7呢？

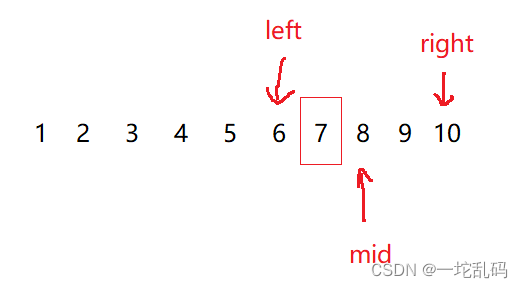
其实也一样写，把right更新到mid前面一位就行，然后在更新mid的值。

right = mid - 1;

当然我们不可能执行一次就结束了，所以要写成一个循环，但是循环终止的条件是什么呢？
仔细观察可以看到，要么是left在向右移动，right再向左移动，也就是说指向left在right左边，就说明两个下标之间肯定有元素，有元素就说明还没有找完。所以终止条件无非就两种left > right的时候或者找到需要找的值的时候。

这里要注意必须是left > right因为除了left < right的时候，left==right的时候也要判断，因为很有可能key的值就是left,right相等的时候。如果循环条件写成left < right就会把这种条件忽略掉。

int search(int* nums, int numsSize, int target) {
    int begin = 0;
    int end = numsSize - 1;
    int mid = (begin + end) / 2;
    while (begin <= end)
    {
        if (nums[mid] < target)
            //说明此时要找的位置在中间位置右边
        {
            begin = mid + 1;
        }
        else if (nums[mid] > target)
            //说明此时要找的位置在中间位置左边
        {
            end = mid - 1;
        }
        else
            //如果相等说明找到了
        {
            return mid;
        }
        mid = (begin + end) / 2;
    }
    //循环结束还没有找到就返回-1
    return -1;
}

这里还有一个小细节，这里的mid的值我是这样写的：

int mid = (begin + end) / 2;

这样写虽然可以，但是有一定的风险，因为mid是int类型的，但此时begin,end都是很大的时候就很有可能得到的值mid装不下，导致发生错误。所以这里改进一下：

int mid = begin + (end - begin)/2;

二.第一个错误的版本

原题传送门：力扣

题目：

有序序列中查找常用的就是二分查找了。这题也不例外，假设这里有10个产品，同样定义三个变量来表示数组元素下标：

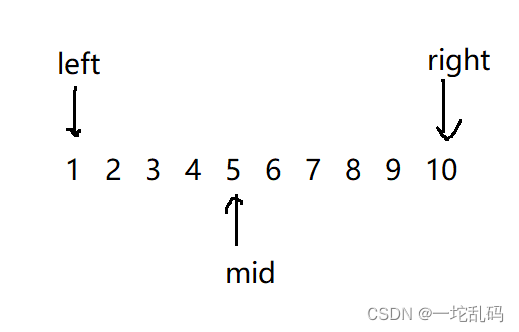
现在要找的第一个错误版本要保证它的前一个版本是正确的。这里假设第一个错误版本是8，所以mid和mid之前的版本都是正确的。现在就可以更新一下left的值，因为mid肯定是正确的了，所以left改到mid后面一个位置就行，然后更新mid的位置：

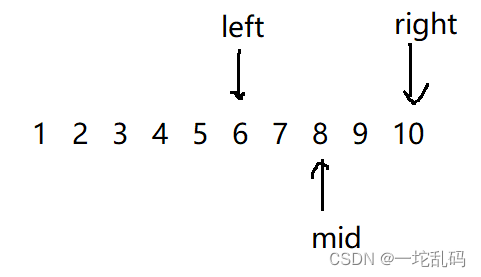
随后发现此时mid指向的版本号是错误的，说明此时mid或者mid的前几个里有一个是第一个错误的版本，此时改更新right的位置成mid，随后在更新mid：

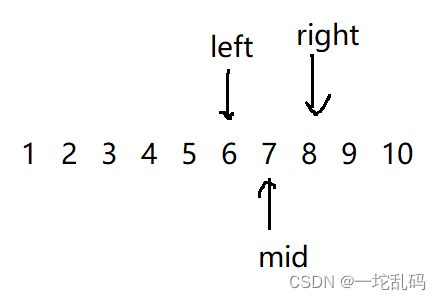
当初假设的8是第一个错误版号，mid指向的版号是正确的，所以继续更新：

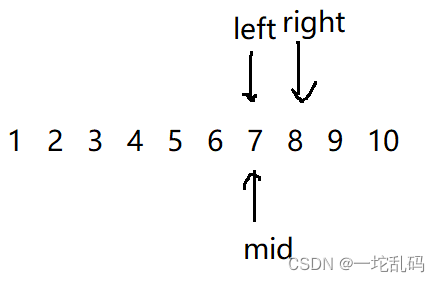
mid指向的仍然是正确版号，所以继续走：

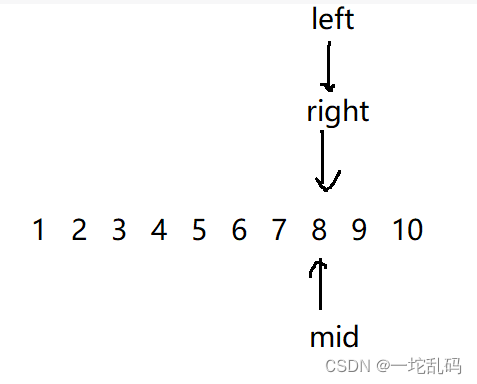
因为不可能一次就把答案找到，肯定要把上面的步骤放在一个循环里，通过上图，循环的终止条件也显而易见了。下面这是答案代码：

int firstBadVersion(int n) {
    int left = 1;
    int right = n;

    while(left < right)
    {
        int mid = left + (right - left) / 2;
        //int mid = (left + right) / 2;
        if(isBadVersion(mid) == true)
            right = mid;
        else
            left = mid + 1;
    }
    return left;
}

三.搜索插入位置

原题传送门：力扣

题目：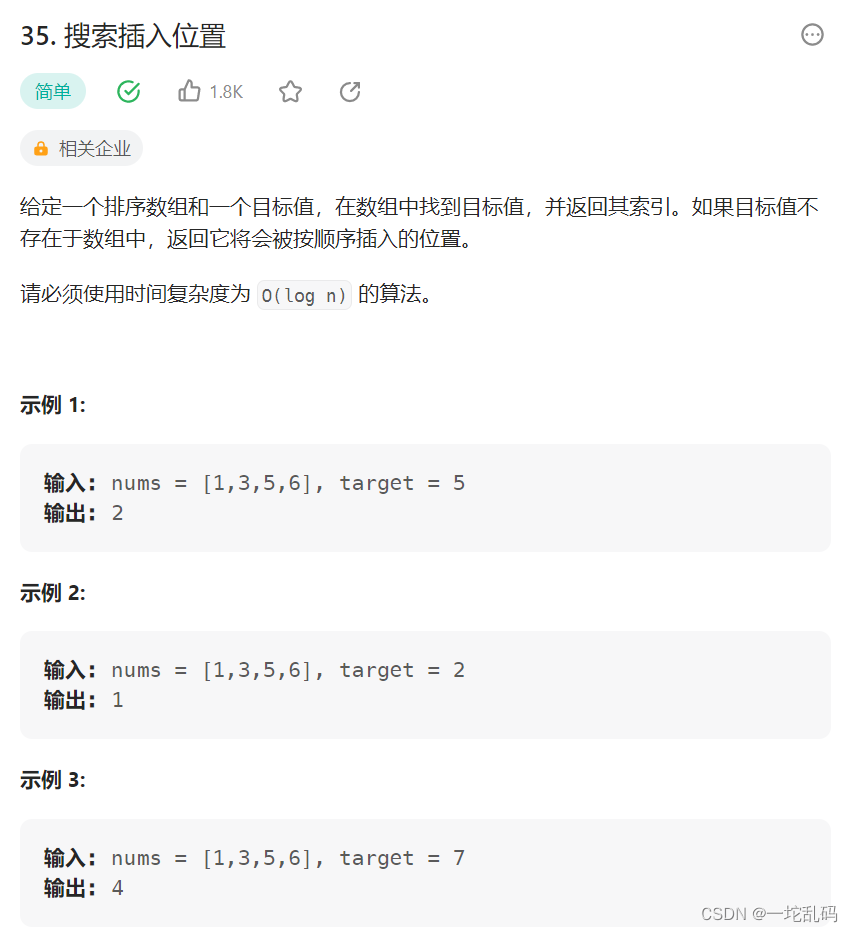

这其实和第一题的普通二分查找差不多，只是这里多了一个条件，如果在数组中找不到对应的target就把target插到对应的位置，并返回其下标。我们就看上面的三个例子就可以了，前两个例子可以不用管就是二分查找，现在主要看第三个例子：找不到target的情况。

做这一题可以先找规律，就当这个例三是个普通二分查找的题目，看看最后的情况和target有什么关系：

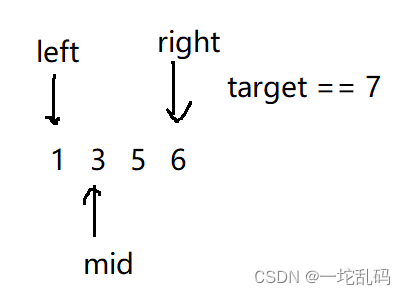
经过一系列变化，如果a[mid]<target，left更新到mid+1的位置，a[mid]>target，right更新到mid-1的位置,然后一直循环直到left >right时停下来.(上面这些都和第一题一样，这里就不细讲了)。最后的图：

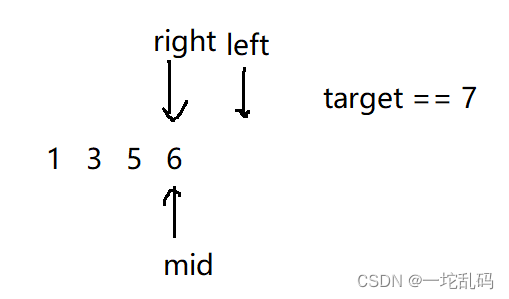
按照第一题的写法，本应该走到这一步并跳出循环的时候应该要返回一个false，但是这里不同，如果你没有找到target是把target插入进去并把它的下标返回出来。但是通过上图可以发现，需要返回的答案其实就是left的值是吧。但是题目没说要检查target是否被插入到数组中，所以说如果没有找到直接返回left就行了：

int searchInsert(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize - 1;
    int mid = (left + right) / 2;

    while (left <= right)
    {
        mid = (left + right) / 2;
        if (nums[mid] < target)
            left = mid + 1;
        else if (nums[mid] > target)
            right = mid - 1;
        else
            return mid;
    }
    return left;
}

有人可能会觉得，我上面举得例子是个巧合，只是刚好答案是left的值。其实不是的，这并不是一个巧合，while循环结束的条件是left > right，也就是说最后都没有找到target的时候肯定会跳出循环，而跳出循环后，left,right的关系肯定是left = right+1.而target要插入的位置肯定是循环里最后一次找的值的后面一个也就是right指向元素的后一个。所以答案自然就是left的值了。