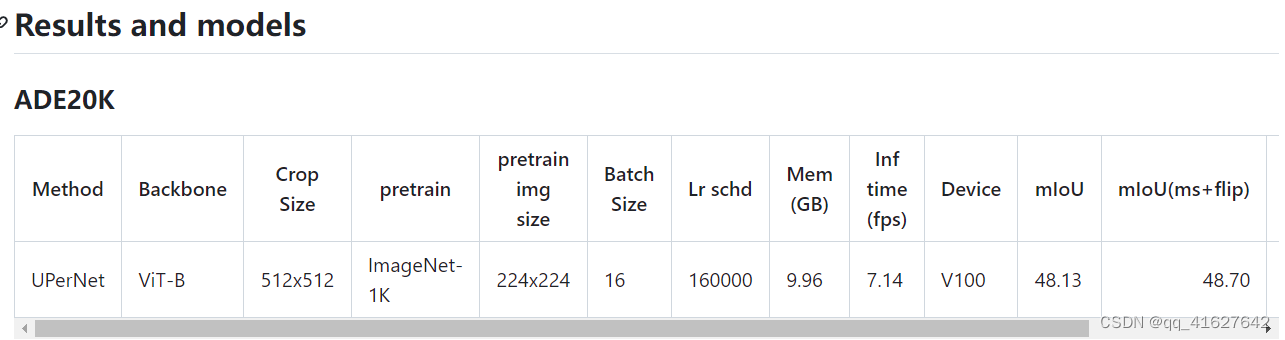
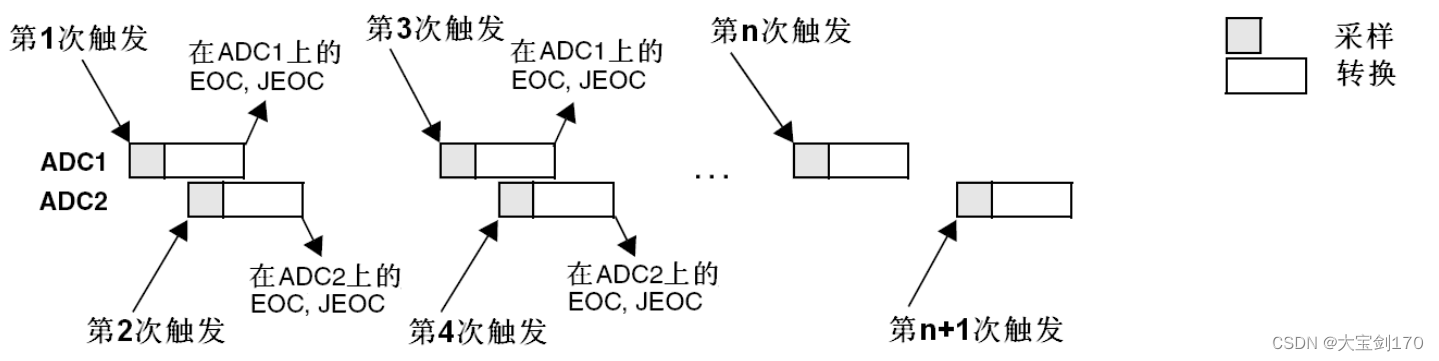
#647 回文子串
自己不会做。 之前遇到的大部分题目是,我们求什么dp里面就放什么。但这道回文的题不是:"
本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。" 但根据回文性质,可以有"bool dp[i][j]:区间范围[i,j] (左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。"

result就是统计回文子串的数量。注意没有列出当s[i]与s[j]不相等的时候,因为在下面dp[i][j]初始化的时候,就初始为false。 初始化:一开始都是false
遍历顺序:本题遍历顺序和以往大部分不同。遍历顺序我们一般先得出递推公式,然后看是什么方向推什么方向,以往都是左上推导出右下。但是本题 dp[i+1][j-1] 在 i j 的左下,所以是左下推右上,顺序是下到上,左到右
因为dp[i][j]的定义,所以j一定大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。
int countSubstrings(string s) {
vector<vector<bool>> dp(s.size(),vector<bool>(s.size(),false));
int res=0;
for(int i=s.size()-1;i>=0;i--){//bottom to up
for(int j=i;j<s.size();j++){//left to right
if(s[i]==s[j]){
if(j-i<=1) {
dp[i][j]=true;
res++;
}
else if(dp[i+1][j-1]){
dp[i][j]=true;
res++;
}
}
}
}
return res;
} 还有双指针法,空间复杂度会小一点。
void extend(string &s, int i, int j, int &res){
while(i>=0 && j<s.size() && s[i]==s[j]){
res++;
i--;
j++;
}
}
int countSubstrings(string s) {
int res=0;
for(int i=0;i<s.size();i++){
extend(s,i,i,res);
extend(s,i,i+1,res);
}
return res;
} #516 最长回文子序列
看的随想录的,自己又实现了一遍。本题注意是序列,是可不连续的
dp[i][j]含义是 在i左闭j右开 区间里 的回文最大长度
递推公式:相等就是里面那个更小的情况额外加新的开头和结尾就是+2;
"如果s[i]与s[j]不同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。 加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);"
易错:遍历顺序和上一道题一样是左下到右上的,所以找最后的值就不是找//return dp[s.size()-1][s.size()-1];这个,而是 return dp[0][s.size() - 1]; 右上方的才对。
我其实想不明白为什么内层for是j=i+1开始而不是i,i会runtime error,问了gpt也没懂
我还问了gpt一个,计算会基于一些左下方没意义的方块,为什么合理:好像懂了,但又没全懂,下次再想想


int longestPalindromeSubseq(string s) {
vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));
for(int i=0;i<s.size();i++){
dp[i][i]=1;
}
for(int i=s.size()-1;i>=0;i--){
for(int j=i+1;j<s.size();j++){
if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1]+2;
else dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
}
}
//return dp[s.size()-1][s.size()-1];
return dp[0][s.size() - 1];
}