目录
1 先说结论:
2 Σ几何分布的P(x=n) = P(n次试验至少成功1次)
2.1 几何分布的概率
2.2 这个是可以证明的,下面是推导过程
2.3 怎么理解呢?
3 另外,P(累计成功k次)= ΣP(成功k次的二项分布)
3.1 成功k次的概率 和 累计成功k次概率
3.2 成功k次的概率 和 至少累计成功k次概率
3.3 这个不需要像上面需要证明,是不言自明的
4 各种概率
5 应用,暂缺,以后再补吧
1 先说结论:
- 结论1:Σ几何分布的P(x=n) = P(n次试验至少成功1次)
- ΣP前n-1次失败最后1次成功(x=n)= P(n次试验至少成功1次)
- 结论2:P(累计成功k次)= ΣP(成功k次)
2 Σ几何分布的P(x=n) = P(n次试验至少成功1次)
2.1 几何分布的概率
- Σ几何分布的P(x=n) = P(n次试验至少成功1次)
- ΣP前n-1次失败最后1次成功(x=n)= P(n次试验至少成功1次)
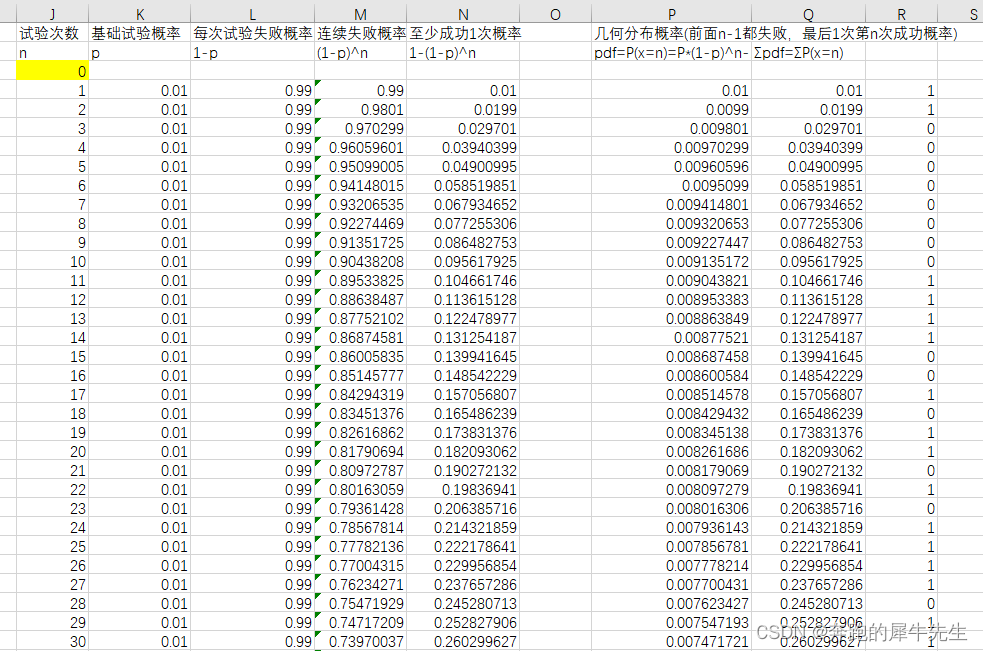
- 我们计算几何概率时,很容易发现这么一个特点
- 从下表可看出
- 左边是先算的连续失败概率---进而推导出,至少成功1次概率=1-连续失败概率
- Σ几何分布的概率 = 至少成功一次的概率
- 这是为什么呢?
2.2 这个是可以证明的,下面是推导过程
下面试图证明:试验n次,P(至少成功1次) =Σp(几何分布)
P(至少成功1次概率)
- =1-P(连续失败的概率)
- =1-p(失败)*p(失败)*....*p(失败)
- =1-(1-p)^n
Σp(几何分布概率之和)
- =p*p(失败)^0+p*p(失败)^1+p*p(失败)^2+p*p(失败)^3+....+p*p(失败)^(n-1)
- =p*(1-p)^0+p*(1-p)^1+p*(1-p)^2+p*(1-p)^3+....+p*(1-p)^(n-1)
- =p*((1-p)^0+(1-p)^1+(1-p)^2+(1-p)^3+....+(1-p)^(n-1))
- 因为后面是等比数列,而且从0到n-1就是n个
- =p*(1-(1-p)^n)/(1-(1-p)))
- =p*(1-(1-p)^n)/(1-(1-p)))
- =p*(1-(1-p)^n)/p
- =1-(1-p)^n
证明完毕
2.3 怎么理解呢?
- P(n次试验至少成功1次) = Σ几何分布的P(x=n) = ΣP前n-1次失败最后1次成功(x=n)
- P(n次试验至少成功1次) = P(x=0) + P(x=1) +....+ P(x=n)
- 1- P(连续失败概率) = P(x=0) + P(x=1) +....+ P(x=n)
- 尝试这样进行理解,不知道对不对
- 右边的反面
- =ΣP前n-1次失败最后1次成功(x=n) 的反面
- = P(x=0) + P(x=1) +....+ P(x=n) 的反面
- = (1-P(x=0)) + (1-P(x=1) )+....+(1- P(x=n))
- = (1-共1次P前0次都失败第1次成功) + (1-共2次P前1次都失败第2次成功)+ ... ...+ (1-共n次P前n-1次都失败第n次成功)
- = (共1次P前0次都失败第1次也失败) + (共2次P前1次都失败第2次也失败) + ... ...+ (共n次P前n-1次都失败第n次也失败)
- =共1次全失败+共2次全失败+ ... ...+共n次全失败
- =全部连续失败的概率
3 另外,P(累计成功k次)= ΣP(成功k次的二项分布)
3.1 成功k次的概率 和 累计成功k次概率
- 因为试验n次,成功k次概率是二项分布
- 因此 P(累计成功k次) = ΣP(成功k次)= ΣP(二项分布)
- 比如累计成功3次,P(累计成功k次) = ΣP(成功k次) (k=1...3)
3.2 成功k次的概率 和 至少累计成功k次概率
- 因为试验n次,成功k次概率是二项分布
- 因此 P(累计成功k次) = ΣP(成功k次)= ΣP(二项分布)
- 比如累计成功3次,P(累计成功k次) = ΣP(成功k次) (k=1...3)
- 比如至少累计成功8次,也就是累计成功8次及以上,P(至少累计成功k次) = 1-ΣP(成功k次) (k=1...7)
3.3 这个不需要像上面需要证明,是不言自明的
- 因为累计概率= Σ 成功k次 (k=1,n)
4 各种概率
- 试验n次,连续成功概率
- 试验n次,连续失败概率
- 试验n次,至少失败1次概率
- 试验n次,至少成功1次概率
- 试验n次,最后一次成功概率:对应几何分布
- 试验n次,成功k次概率:对应二项分布
- 试验n次,累计成功k次概率 和 至少累计成功k次概率
试验前提:试验次数n, 单次试验内成功次数是p
- 连续成功概率,从1~n,p*p*p*....*p
- 连续失败概率,从1~n,(1-p)*(1-p)*(1-p)*....*(1-p)
- 至少失败1次的概率,从1~n,1-p*p*p*....*p
- 至少成功1次的概率,从1~n,1-(1-p)*(1-p)*(1-p)*....*(1-p)
- 最后1次成功的概率,几何分布 P(x=n)=p*(1-p)^(n-1)
- 当n取值范围从1~n时
- P(x=1)=p*(1-p)^0
- P(x=2)=p*(1-p)^1
- ... ...
- P(x=n)=p*(1-p)^(n-1)
- 试验n次前提下,成功k次的概率,二项分布 P(x=k)=C(n,k)*p^k*(1-p)^(n-k)
- 当k取值范围从0~k时,k<=n
- P(x=0)=C(n,k)*p^0*(1-p)^(n-0)
- P(x=1)=C(n,k)*p^1*(1-p)^(n-1)
- P(x=2)=C(n,k)*p^2*(1-p)^(n-2)
- ... ....
- P(x=k)=C(n,k)*p^k*(1-p)^(n-k)
- 试验n次,累计成功k次概率
- 因为试验n次,成功k次概率是二项分布
- 因此 P(累计成功k次) = ΣP(成功k次)= ΣP(二项分布)
- 试验n次,累计成功k次概率 和 至少累计成功k次概率
- 因为试验n次,成功k次概率是二项分布
- 因此 P(累计成功k次) = ΣP(成功k次)= ΣP(二项分布)
- 比如累计成功3次,P(累计成功k次) = ΣP(成功k次) (k=1...3)
- 比如至少累计成功8次,也就是累计成功8次及以上,P(至少累计成功k次) = 1-ΣP(成功k次) (k=1...7)