主成分分析(PCA)

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OQ2UkQmi-1689528282890)(D:\YHT\SVD博客\13.png)]$

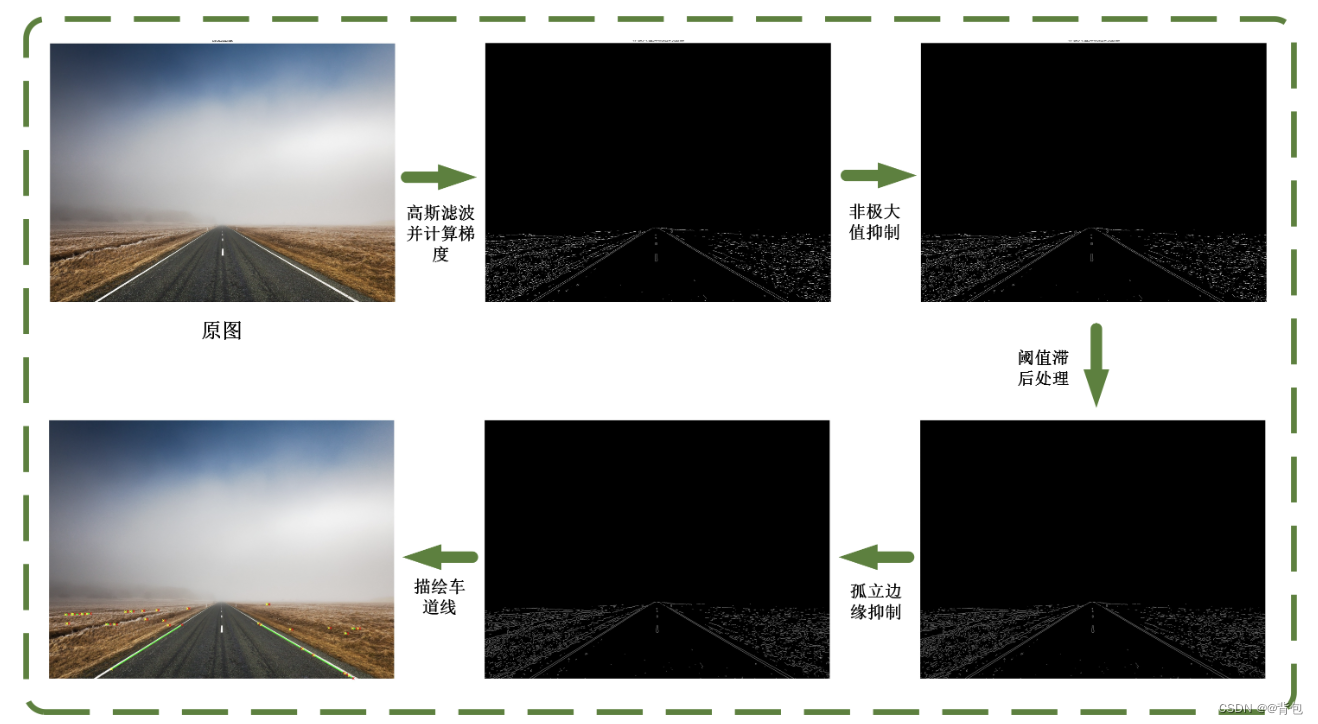
PCA(Principal Component Analysis) 是实现数据降维的一种算法。正如其名，假设有一份数据集，每条数据的维度是d，PCA通过分析这d个维度的前k个主要特征(这k个维度在原有d维特征的基础上重新构造出来，且是全新的正交特征)，将d维的数据映射到这k个主要维度上进而实现对高维数据的降维处理。 PCA算法所要达到的目标是，降维后的数据所损失的信息量应该尽可能的少，即这K个维度的选取应该尽可能的符合原始d维数据的特征。

本篇博客中所有的可视化及数据预处理代码已上传至github：

Machine-Learning/SVD_PCA at main · Scienthusiasts/Machine-Learning (github.com)

1.理论部分

PCA之所以能够实现将数据降维后依然最大程度保持原有数据的特征，主要依赖于对数据集每个维度两两之间的协方差(或方差)分析。

我们知道，协方差可以表示两种数据之间的相关性/分散程度。对数据的不同维度之间进行协方差分析，协方差的绝对值越大，表明两个维度越线性相关，越是相关的两个维度之间的信息熵越低(因为知道一个维度的分布就可以大差不差推出另一个维度的分布)，信息熵越低则意味着合并这两个维度所损失的信息量越小。

因此，PCA通过寻找数据d个维度之间的最佳线性组合，找到其中的某一超平面(使得这一方向数据的方差或协方差最大)作为主成分，将数据投影到这个超平面上[如开头图所示]，将d个存在线性相关性的维度压缩为d-1一个维度(压缩的过程中舍弃的是方差最小的方向)。而对于如何寻找这d个维度之间的最佳线性组合，则可以通过对数据集的协方差矩阵进行特征分解来实现。

而实际情况是，数据集所在的d维空间按照重要程度排序可以有多个主成分，选取其中的前k个最重要的主成分，将d维数据投影到这k个主成分上，舍弃相对不那么重要的d-k个成分，实现数据的降维。

实现PCA有两个基本出发点，一个是最大化投影方差，另一个是最小化投影距离，下面以最大化投影方差为例进行说明。

最大化投影方差

我们首先假设输入n条数据，每个数据原始有d维，以列优先存放，每一列是数据集的一条数据，数据集构成一个d行n列的矩阵X

假设将这d维数据投影到新的坐标轴上的投影矩阵W，W大小为k行d列(k<d)
$X=\left[x_1, x_2, \ldots, x_n\right], \quad W=\left[\begin{array}{c} w_1^{\mathrm{T}} \\ w_2^{\mathrm{T}} \\ \vdots \\ w_k^{\mathrm{T}} \end{array}\right]$
其中W是一个标准正交基，每一行w是一个单位向量，即满足:
$w_i^T w_j=\delta_{i j}=\left\{\begin{array}{l} 1, i=j \\ 0, i \neq j \end{array}\right.$
基于最大化投影方差，PCA的目标是，我们希望降维后还能更多的保留原来数据的信息量，而且降维后不同维度的相关性越小越好，这样去掉某些维度不影响剩余维度。

最大化投影方差(协方差)意在使投影后的数据点之间的方差(协方差)达到最大。首先给出投影之后的方差(协方差)公式,注意这里D(X)其实就是协方差矩阵。
$D(X)=\sum_{i=1}^n\left(W x_i-\text { mean }\right)^2$
一般地，我们会提前将数据每一维度0均值化处理(mean=0)，这样一来，就可以简化后续的推导步骤.
$\begin{aligned} D(X) & =\frac{1}{n-1} \sum_{i=1}^n\left(W x_i\right)^2=\frac{1}{n-1} \sum_{i=1}^n\left(W x_i\right)\left(W x_i\right)^T \\ & =\frac{1}{n-1} \sum_{i=1}^n{W x_ix_i}^T W^T=\frac{1}{n-1}\left(W X X^TW^T\right)=W(\frac{1}{n-1}XX^T)W^T\\ & = WCov(X)W^T \end{aligned}$
我们将协方差矩阵令为 Σ，最大化投影方差等价于：
$max\{ W ΣW^T\}\quad s.t.WW^T=E$

上述带约束的极值问题，可以通过构造拉格朗日函数求解：
$L(W) = -WΣW^T+λ(WW^T-E)$
对W求偏导，得(此处需运用矩阵求导法则)：
$\frac{\partial L(w)}{\partial W}=-2 \Sigma W+2 \lambda W=0 \Longrightarrow \Sigma W=\lambda W$
可以发现，我们所要寻找的投影矩阵W其实是 Σ的特征向量， λ是对应的特征值。

此时最大化投影方差，就等价于：
$max\{ Wλ W^T\}\quad s.t.WW^T=E\Rightarrow max\{ λ\}$
可见，PCA要去寻找的第一主成分，就是使得X的协方差矩阵最大特征值对应的特征向量。

若我们最终想要保留下k个维度，我们就选取前k个最大的特征值对应的特征向量，然后把原始的数据在这些轴上面进行投影即可：
$x^{'}_{i}=\left[\begin{array}{c} w_1^{\mathrm{T}}x_i \\ w_2^{\mathrm{T}}x_i \\ \vdots \\ w_k^{\mathrm{T}}x_i \end{array}\right]\Rightarrow X^{'}=WX$

一般而言，k的选取依照实际情况而定，我们可以通过降维前后的信息占比η来决定k应取多少：
$\eta=\sqrt{\frac{\sum_{j=1}^k \lambda_j^2}{\sum_{i=1}^d \lambda_i^2}}$

基于SVD分解的PCA

求解的协方差矩阵最大特征值对应的特征向量，本质就是对XXᵀ进行特征分解，当然我们也可以通过SVD分解来完成这一操作。

由SVD分解的形式可知：
$X^T=U \Sigma V^T V \Sigma U^T=U \Sigma^2 U^T$
因此XXᵀ的特征值就是奇异值分解后得到的奇异值的平方，特征向量就是左奇异矩阵U中的每一列。

核PCA

值得注意的是，PCA属于线性分析方法，假设数据各个维度之间既不相关也不独立，PCA就有可能失效，比如下面这种数据：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V1y2KCNV-1689528282891)(D:\YHT\SVD博客\14.png)]$

再回顾一下数据的协方差矩阵：
$X^T=\sum_{k=1}^n x_k x_k^T$
可以注意到，在求解协方差矩阵的过程中，出现了XXᵀ的形式，因此我们就可以使用核函数，将原始数据映射到非线性的高维曲面上，在更高维度的曲面上，X或许就是线性可分的。核函数的使用前提和具体形式可以回顾我之前记录的的SVM博客。即：
$X^T=\left[\begin{array}{c} \phi\left(x_1\right)^T \\ \cdots \\ \phi\left(x_N\right)^T \end{array}\right]\left[\phi\left(x_1\right), \cdots, \phi\left(x_N\right)\right]=\left[\begin{array}{ccc} k\left(x_1, x_1\right) & \cdots & k\left(x_1, x_N\right) \\ \vdots & \ddots & \vdots \\ k\left(x_N, x_1\right) & \cdots & k\left(x_N, x_N\right) \end{array}\right]$
$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SkKetGto-1689528282891)(D:\YHT\SVD博客\15.png)]$