英文题目：Perfect Match: A Simple Method for Learning Representations For Counterfactual Inference With Neural Networks

翻译：完美匹配：一种简单的神经网络反事实推理学习表示方法

单位：

论文链接：https://arxiv.org/pdf/1810.00656.pdf

代码：

摘要：从观测数据中学习反事实推理的表示对于许多领域(如医疗保健、公共政策和经济)具有很高的实际意义。反事实推理使人们能够回答“如果...？”问题，例如“如果我们给这个患者治疗，结果会是什么？”。然而，目前训练神经网络对观测数据进行反事实推断的方法要么过于复杂，仅限于只有两个可用处理的设置，要么两者都受到限制。在这里，我们提出了完美匹配 (PM)，这是一种训练神经网络进行反事实推理的方法，易于实现，与任何架构兼容，不会增加计算复杂度或超参数，并扩展到任意数量的处理。PM 基于用倾向匹配的最近邻在小批量中增加样本的想法。我们的实验表明，PM 在跨多个基准推断反事实结果方面优于许多更复杂的最先进方法，尤其是在具有许多治疗的设置中。

目录

1介绍

2 相关工作

3 方法论

4 实验我们旨在回答以下问题：

 5 结果与讨论反事实推理

6 结论

---

1介绍

从观测数据估计个体治疗效果1(ITE)是许多领域的一个重要问题。例如，在医学中，我们有兴趣使用过去治疗的人的数据来预测哪些药物会导致新患者更好的结果 [1]。同样，在经济学中，一个潜在的应用程序将是确定某些作业程序将基于过去作业培训程序的结果的有效性。

由于两个原因，来自观测数据的ITE估计是困难的：首先，我们从未观察到所有潜在的结果。如果患者接受了治疗她的症状的治疗，我们从未观察到如果患者在同一情况下规定了潜在的替代治疗，会发生什么。其次，将病例分配给治疗通常是有偏见的，因此给定治疗更有效的情况更有可能接受该治疗。因此，治疗组和总体人群之间的样本分布可能存在显着差异。经过训练以最小化事实错误的监督模型naïvely 会过度拟合治疗组的属性，因此不能很好地推广到整个人群。

为了解决这些问题，我们引入了完美匹配 (PM)，这是一种用于训练神经网络进行反事实推理的简单方法，可以扩展到任意数量的处理。PM通过与其他处理的倾向分数最接近的匹配来增强小批量内的每个样本，有效地控制了观测数据中治疗的偏差分配。PM 易于与现有的神经网络架构一起使用，易于实现，并且不添加任何超参数或计算复杂度。我们通过实验来证明PM对高水平的治疗分配偏差具有鲁棒性，并且在跨多个基准数据集推断反事实结果方面优于许多更复杂的最先进的方法。这项工作的源代码可在 https://github.com/d909b/fect_match 获得。

贡献。这项工作包含以下贡献：

• 我们引入了完美匹配 (PM)，这是一种基于小批量匹配的简单方法，用于学习具有任意数量的处理设置的反事实推理的神经表示。

• 我们开发了性能指标、模型选择标准、模型架构和开放基准，用于在具有多种可用处理的情况下估计单个治疗效果。

• 我们在具有两个或更多处理的设置中对半合成、真实世界的数据进行了广泛的实验。实验结果表明，PM在从观测数据推断反事实结果方面优于许多更复杂的最先进的方法。

2 相关工作

背景。推断干预措施的因果影响是许多重要领域的核心追求，例如医疗保健、经济学和公共政策。例如，在医学中，治疗效果通常通过严格的前瞻性研究来估计，例如随机对照试验 (RCT)，其结果用于调节治疗的批准。然而，在许多感兴趣的环境中，随机实验执行起来过于昂贵或耗时，或者出于伦理原因不可能[3,4]。另一方面，观察数据（即未在随机实验中收集的数据）通常大量可用。在这种情况下，从观测数据估计因果效应的方法至关重要。

估计个体治疗效果。由于它们的实际重要性，存在多种方法来从观测数据中估计个体治疗效果。然而，它们主要集中在最基本的设置上，只有两种可用的治疗方法。匹配方法是估计 ITEs 在概念上最简单的方法之一。匹配方法使用相对于度量空间接收到的 t 的最近邻的事实结果来估计样本 X 相对于治疗 t 的反事实结果。这些k-Nearest-Neighbour (kNN)方法[5]工作在潜在的高维协变量空间中，因此可能会受到维数[6]的诅咒的影响。倾向得分匹配(PSM)[7]通过在给定协变量X的t的标量概率p(t|X)上匹配来解决这个问题。另一类估计个体治疗效果的方法是调整回归模型，该模型将治疗和协变量的回归模型作为输入。线性回归模型既可以用于构建一个模型，将处理作为输入特征，也可以使用多个单独的模型，每个处理一个[8]。更复杂的回归模型，例如治疗不可知表示网络 (TARNET) [1] 可用于捕获非线性关系。将结果模型和治疗倾向模型结合起来的方法，其方式对两者的错误指定具有鲁棒性，称为双重鲁棒[9]。基于树的方法训练许多弱学习器来构建富有表现力的集成模型。基于树的方法的例子是贝叶斯加性回归树 (BART) [10, 11] 和因果森林 (CF) [12]。表示学习方法试图学习一个高级表示，其中协变量分布在治疗组之间平衡。表示平衡方法的例子是平衡神经网络[13]，它试图通过最小化治疗组之间的差异距离[14]和使用Wasserstein距离等不同指标的反事实回归网络(CFRNET)[1]来找到这种表示。倾向辍学(PD)[15]根据每个样本的治疗倾向调整训练过程中的正则化。

用于推断个性化治疗效果 (GANITE) [16] 的生成对抗网络解决了使用反事实和 ITE 生成器的 ITE 估计。GANITE 使用具有许多超参数和子模型的复杂架构，这些架构可能难以实施和优化。因果多任务高斯过程 (CMP) [17] 将多任务高斯过程应用于 ITE 估计。CMGPs的优化涉及O(n3)复杂度的矩阵反演，这限制了它们的可扩展性。

与现有方法相比，PM 是一种简单的方法，可用于在任意数量的处理的情况下从观测数据中训练富有表现力的非线性神经网络模型进行 ITE 估计。PM 易于实现，与任何架构兼容，不会增加计算复杂度或超参数，并扩展到任意数量的处理。虽然 PM 背后的潜在思想简单而有效，但据我们所知，尚未探索。

3 方法论

异质效应估计的精度(PEHE)。我们在训练模型估计ITE时优化的主要指标是PEHE[23]。

 

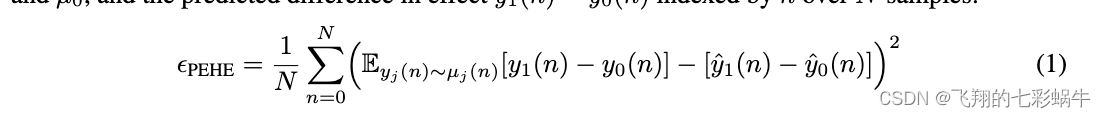
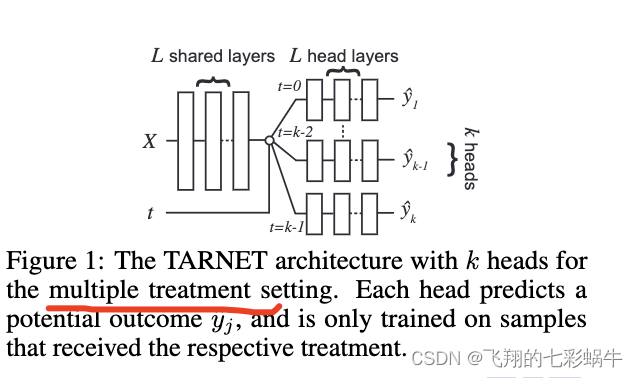
 模型架构。在尝试学习反事实推理的表示时，所选架构在神经网络的性能中起着关键作用。

完美匹配 (PM)。我们考虑通过小批量随机梯度下降 (SGD) 优化的完全可微神经网络模型 ^f 来预测给定样本 x 的潜在结果 ^Y。为了解决观测数据中固有的治疗分配偏差，我们建议在一个空间中执行 SGD，该空间近似于使用平衡分数概念的随机实验。在未混淆假设下，平衡分数具有在给定平衡分数的情况下，治疗分配是不混淆的属性。

算法 1 完美匹配 (PM)。增强后，每批包含来自每个治疗的相同数量的样本，跨治疗的协变量xi近似平衡。

输入：具有指定处理 t 的 B 个随机样本 Xbatch 的批次、N 个样本的训练集 Xtrain、处理选项的数量 k、倾向分数估计器 EPS 来计算给定样本 XOutput 分配的处理概率 p(t|X)

输出：由 B × k 匹配样本组成的批次

4 实验我们旨在回答以下问题：

（1）与现有的最先进方法相比，PM 在推断二元和多处理设置中的反事实结果方面的比较性能是什么。

(2) NN-PEHE 的模型选择是否优于事实 MSE 的选择。

(3)小批量中匹配样本的相对数量如何影响性能。

(4) PM 处理观测数据中处理分配偏差的程度如何。

(5) 与数据集级匹配相比，小批量匹配的学习动态如何？

 5 结果与讨论反事实推理

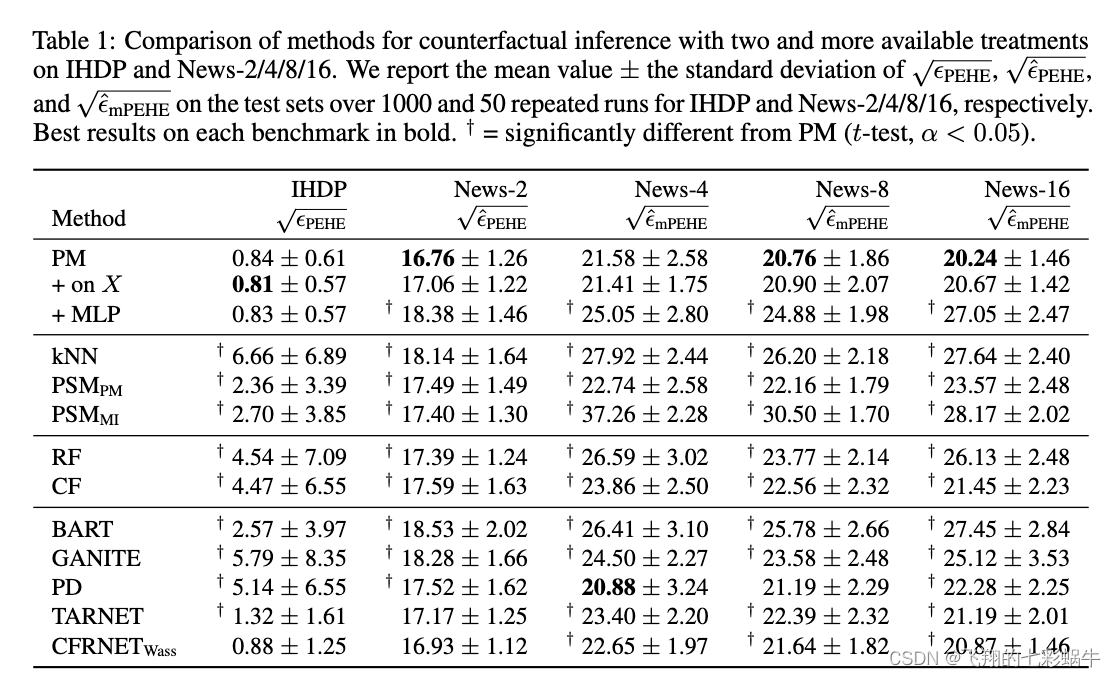
我们使用两个或多个可用处理评估了列出的模型的反事实推理性能（表 1，附录表 S3 中的 ATE）。

 

6 结论

我们提出了 PM，这是一种训练神经网络的新方法，用于从扩展到任意数量的可用治疗的观测数据中估计 ITEs。此外，我们将 TARNET 架构和 PEHE 度量扩展到具有两个以上处理的设置，并引入了 PEHE 和 mPEHE 的最近邻近似，可用于模型选择，而无需访问反事实结果。我们对几个真实世界和半合成数据集进行了实验，结果表明 PM 在推断反事实结果方面优于许多更复杂的最先进方法。我们还发现 NN-PEHE 与真实 PEHE 的相关性明显优于 MSE，因为每个 minibatch 中包含更多匹配的样本可以提高反事实表示的学习，并且 PM 比现有的最先进的方法更好地处理治疗分配偏差。PM 可用于任何处理量的设置，与任何现有的神经网络架构兼容，易于实现，并且不会引入任何额外的超参数或计算复杂性。用于学习反事实表示的灵活和富有表现力的模型，可以推广到具有多个可用处理的设置，可以潜在地促进从医疗保健、经济学和公共政策等几个重要领域的观测数据中得出有价值的见解。